Об аксиомах планиметрии

Аксиомы планиметрии

9 класс

Геометрия Евклида

Геометрия Евклида Первым систематическим изложением геометрии, дошедшим до нашего времени, являются “Начала” – сочинения александрийского математика Евклида.

Спустя много лет в 19 веке русский математик Николай Иванович Лобачевский пересмотрел геометрию Евклида, построил свою геометрию, она приобрела современный вид, которую мы изучаем сейчас.

• Планиметрия (от лат. planum — плоскость, др.-греч. ) — раздел геометрии, изучающий двумерные (одноплоскостные) фигуры, то есть фигуры, которые можно расположить в пределах одной плоскости.
• Основными геометрическими фигурами на плоскости являются точка и прямая .
• Аксиомами называются те основные положения геометрии, которые принимаются в качестве исходных. 

Аксиомы взаимного расположения точек и прямых: 

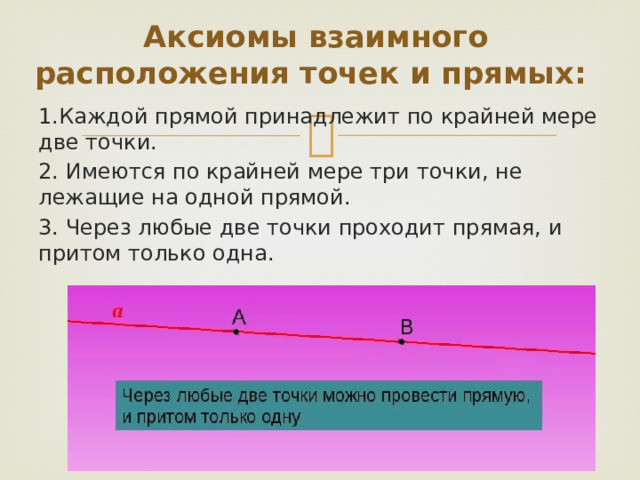
1.Каждой прямой принадлежит по крайней мере две точки.

2. Имеются по крайней мере три точки, не лежащие на одной прямой.

3. Через любые две точки проходит прямая, и притом только одна.

Аксиомы расположения точек на прямой:

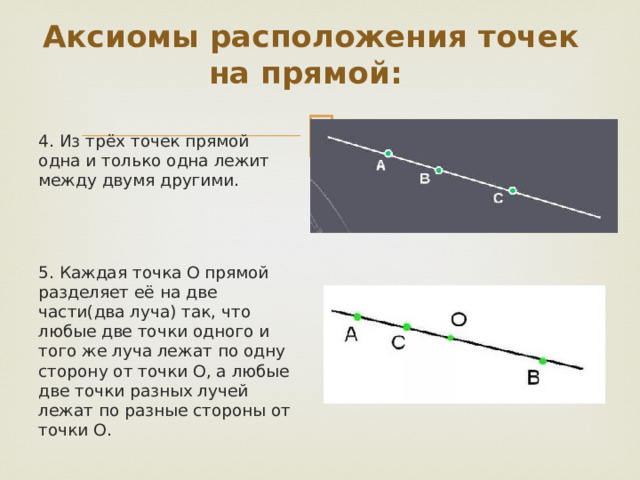
4. Из трёх точек прямой одна и только одна лежит между двумя другими.

5. Каждая точка О прямой разделяет её на две части(два луча) так, что любые две точки одного и того же луча лежат по одну сторону от точки О, а любые две точки разных лучей лежат по разные стороны от точки О.

Аксиома расположения точек на плоскости:

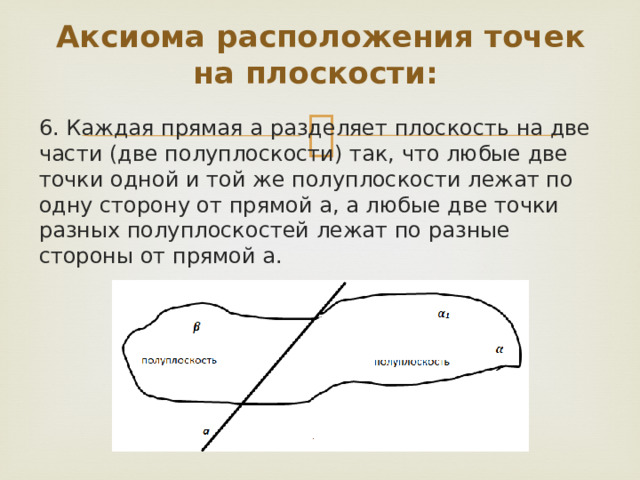
6. Каждая прямая а разделяет плоскость на две части (две полуплоскости) так, что любые две точки одной и той же полуплоскости лежат по одну сторону от прямой а, а любые две точки разных полуплоскостей лежат по разные стороны от прямой а.

Аксиомы наложения или равенства фигур.

Наложение – это отображение плоскости на себя.

Если существует наложение, при котором фигура Ф отображается на фигуру Ф1, то говорят, что фигуру Ф можно совместить наложением с фигурой Ф1, или фигура Ф равна фигуре Ф1.

Аксиомы наложения или равенства фигур:

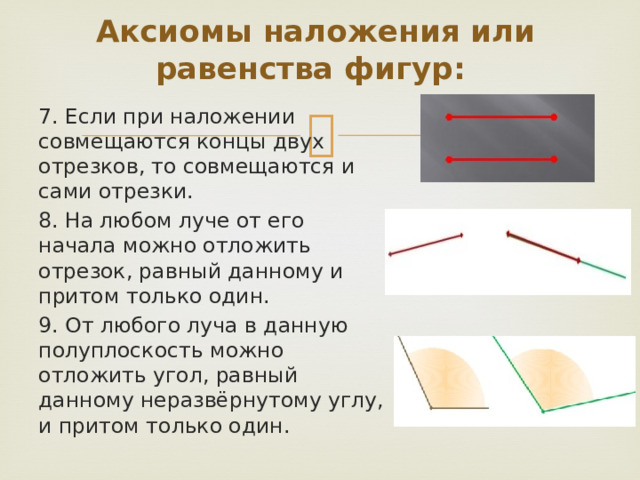
7. Если при наложении совмещаются концы двух отрезков, то совмещаются и сами отрезки.

8. На любом луче от его начала можно отложить отрезок, равный данному и притом только один.

9. От любого луча в данную полуплоскость можно отложить угол, равный данному неразвёрнутому углу, и притом только один.

Аксиомы наложения или равенства фигур:

10. Любой угол hk можно совместить наложением с равным ему углом h1k1 двумя способами: 1)так, что луч h совместится с лучом h1, а луч k – с лучом k1; 2) так, что луч h совместится с лучом k1, а луч k – с лучом h1 .

• 11. Любая фигура равна сама себе.

Аксиомы наложения или равенства фигур:

12. Если фигура Ф равна фигуре Ф1, то фигура Ф1 равна фигуре Ф.

13. Если фигура Ф1 равна фигуре Ф2, а фигура Ф2 равна фигуре Ф3, то фигура Ф1 равна фигуре Ф3.

Аксиомы измерения отрезков:

14. При выбранной единице измерения отрезков длина каждого отрезка выражается положительным числом.

Аксиома существования отрезка данной длины:

• 15. При выбранной единице измерения отрезков для любого положительного числа существует отрезок, длина которого выражается этим числом.

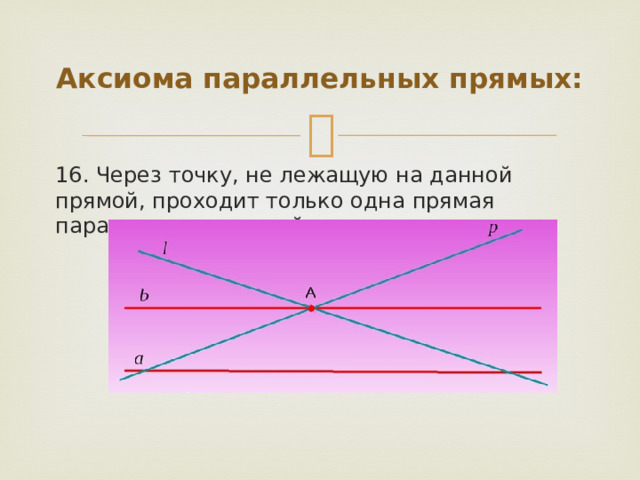
Аксиома параллельных прямых:

16. Через точку, не лежащую на данной прямой, проходит только одна прямая параллельная данной.