Объем прямоугольного параллелепипеда

Действия учителя

Действия ученика, его предполагаемый ответ

1. Организационный момент

Взаимное приветствие; проверка подготовленности учащихся к уроку (рабочее место, внешний вид); проверка отсутствующих.

2. Актуализация знаний

Давайте посмотрим на доску и поработаем с вами устно.

Вычислите примеры и расшифруйте слово.

1. 9	А
   51	Л
   41	Н
   1000	Д
   49	П
   45	Е
   0	Р
   8	И
   16	Ж
   6	К
   52	М

   51-2=

2. 99:11=

3. 16·0=

4. 3²=

5. 3·17=

6. 17+34=

7. 80-35=

8. 51·1=

9. 15·3=

10. 60-11=

11. 2³=

12. 30+19=

13. 90:2=

14. 125·8=

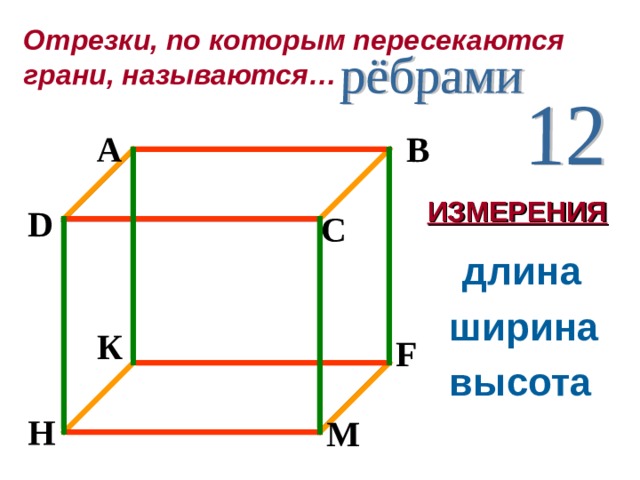
Молодцы!! Справились с этим заданием.

Давайте вспомним, что представляет собой прямоугольный параллелепипед.

Назовите мне, пожалуйста, предметы, которые имеют форму прямоугольного параллелепипеда.

Слайд № 1

Из каких же элементов состоит прямоугольный параллелепипед?

Хорошо.

Чем являются грани прямоугольного параллелепипеда?

Ответьте, сколько граней имеет прямоугольный параллелепипед?

Слайд № 2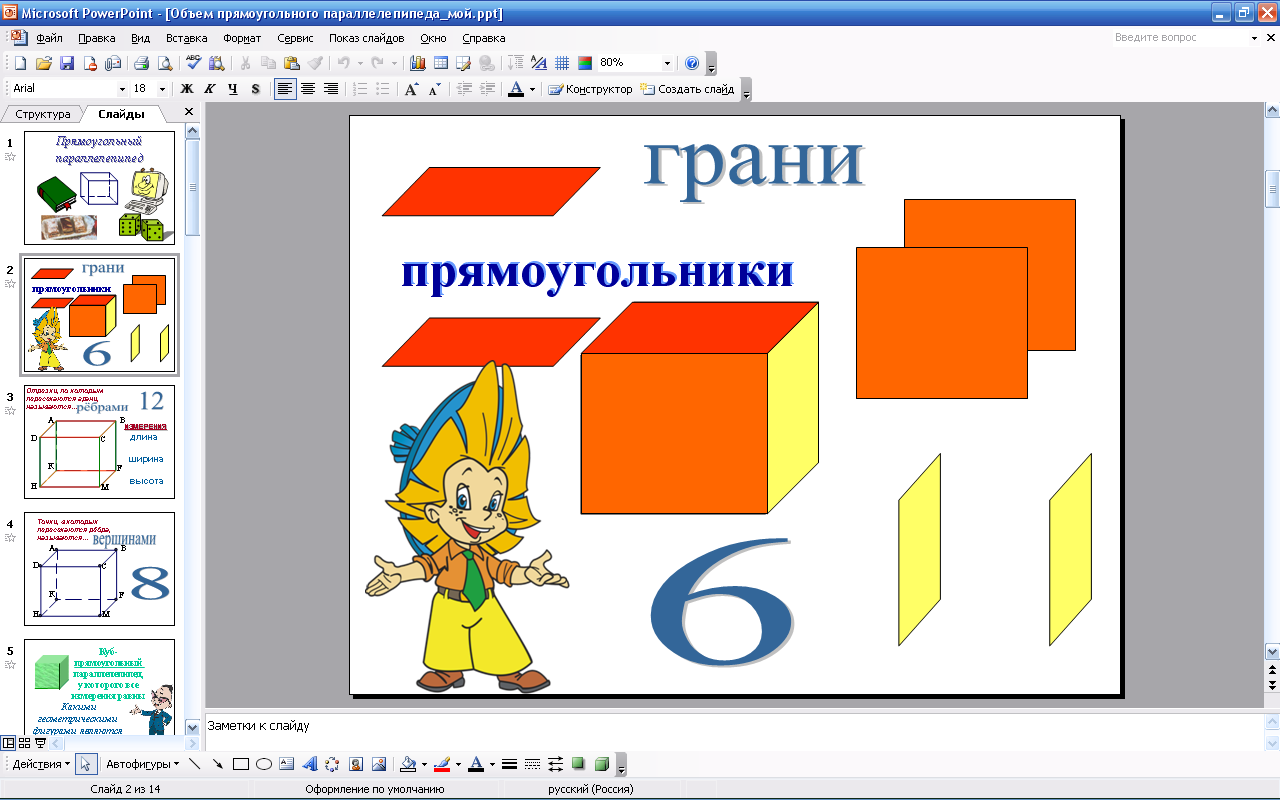

Как называются отрезки, по которым пересекаются грани прямоугольного параллелепипеда?

Слайд № 3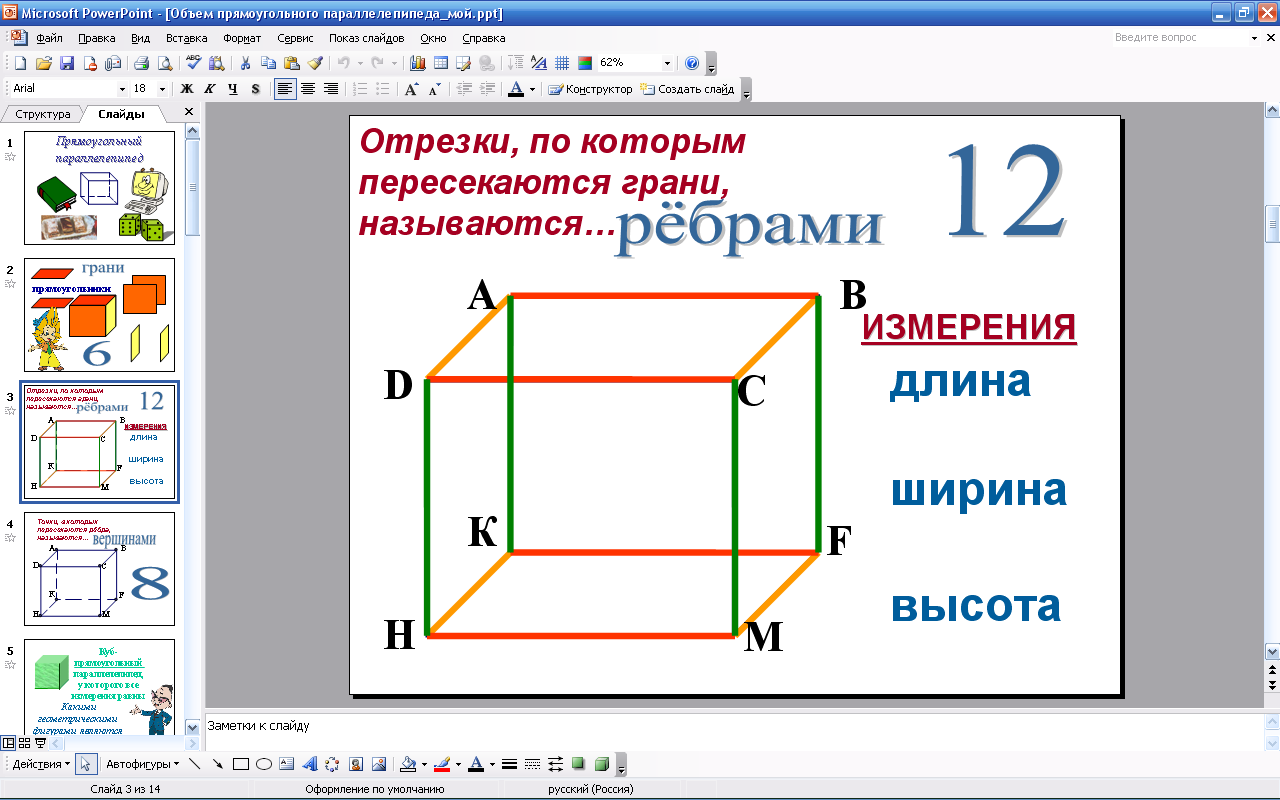

Сколько ребер имеет прямоугольный параллелепипед?

Рёбра тоже имеют свои названия. Какие?

Как ещё по-другому их называют?

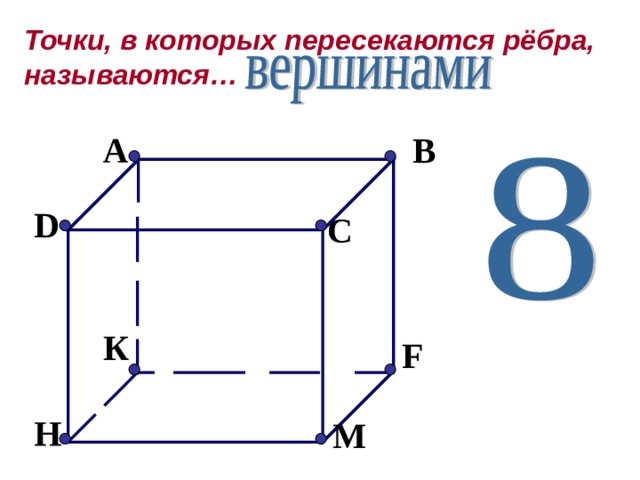
Верно. Молодцы!

И остался у нас ещё один элемент прямоугольного параллелепипеда. Точки, в которых пересекаются рёбра, называются…

Сколько вершин имеет прямоугольный параллелепипед?

Слайд № 4

Назовите вершины прямоугольного параллелепипеда.

Верно.

Слайд № 5

Скажите мне, пожалуйста, а как называется прямоугольный параллелепипед, у которого равны все измерения?

Чем же являются грани куба?

Молодцы!

1. 51-2=49

2. 99:11=9

3. 16·0=0

4. 3²=9

5. 3·17=51

6. 17+34=51

7. 80-35=45

8. 51·1=51

9. 15·3=45

10. 60-11=49

11. 2³=8

12. 30+19=49

13. 90:2=45

14. 125·8=1000

ПАРАЛЛЕЛЕПИПЕД

Ответ: тумбочка, системный блок, ящик

Граней, рёбер и вершин.

Прямоугольниками.

6 граней

Рёбра

12 рёбер.

Длина, ширина и высота

Три измерения прямоугольного параллелепипеда.

Вершинами.

8 вершин

A,B,C,D,K,F,H,M.

Куб.

Каждая грань – квадрат.

3. Объяснение нового материала

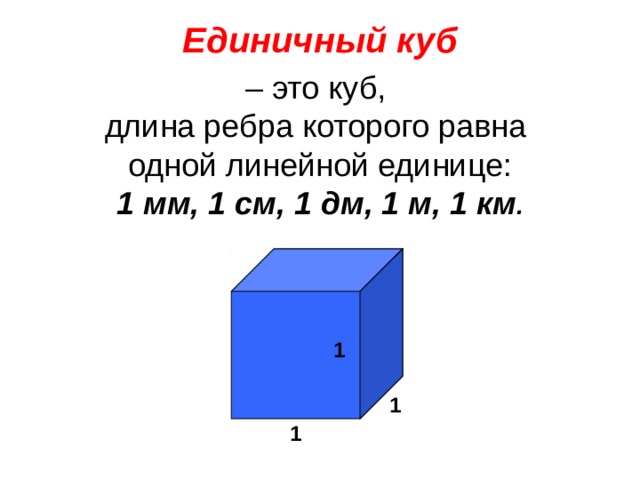
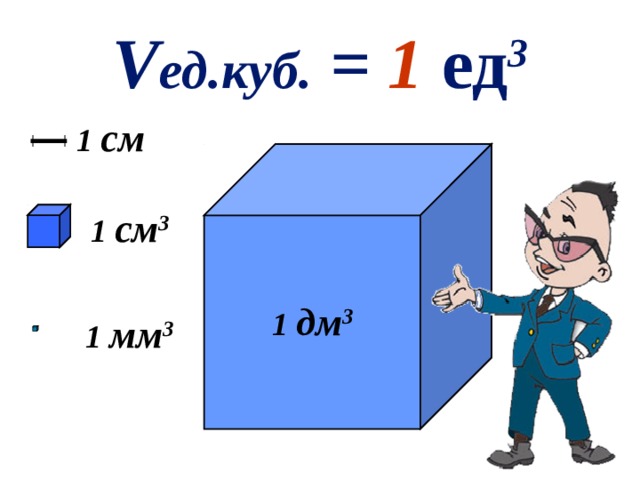
Т ема нашего сегодняшнего урока: «Объём прямоугольного параллелепипеда».

Слайд № 6

В тетрадочках записываем число, классная работа и тему урока.

Ещё в глубокой древности возникла необходимость в измерении количеств различных веществ. Сыпучие вещества и жидкости можно было мерить, наполняя ими сосуды определённой вместимости, т.е. определяя их количество по объёму.

Итак, важным свойством тела является его вместимость, которая характеризуется объёмом.

Как же вычисляют объёмы тел?

Для этого нам нужны единицы объёмов. Интересно, что ещё в Древнем Вавилоне единицами объёмов служили кубы, ребром которых являлись единицы длины. Точно также поступают и сейчас: объём измеряют с помощью кубов, но не любых кубов, а единичных.

Вспомните, когда мы с вами измеряли площадь прямоугольника, мы пользовались таким понятием, как «единичный квадрат». Что это такой за квадрат?

Аналогично, единичный куб – это куб, ребро которого равно

одной линейной единице.

Слайд № 7

Записываем в тетрадях определение: единичный куб – это куб, длина ребра которого равна

одной линейной единице.

За единицу измерения объема принимают объем единичного куба.

Слайд № 8

V_{ед.куба} = 1 ед³

Е

V_{ед.куба} = 1 см³

Е

V_{ед.куба} = 1 мм³

Е

V_{ед.куба} = 1 дм³

Показать куб с ребром 1 дм.

Для измерения объёма применяют следующие единицы: кубический миллиметр (1 мм³), кубический сантиметр (1 см³), кубический метр (1 м³), кубический километр (1 км³).

Как же используют единичные кубы для измерения объёма тел?

Прежде чем ответить на этот вопрос, давай те с вами вспомним: как связаны понятия «единичный квадрат» и «площадь прямоугольника»?

С параллелепипедом похожая ситуация. Если прямоугольный параллелепипед можно разрезать на k единичных кубов, то говорят, что его объём равен k кубическим единицам.

Измерить объём прямоугольного параллелепипеда – значит подсчитать, сколько в нём содержится единичных кубов.

Найдём объём изображённых параллелепипедов.

Слайд № 9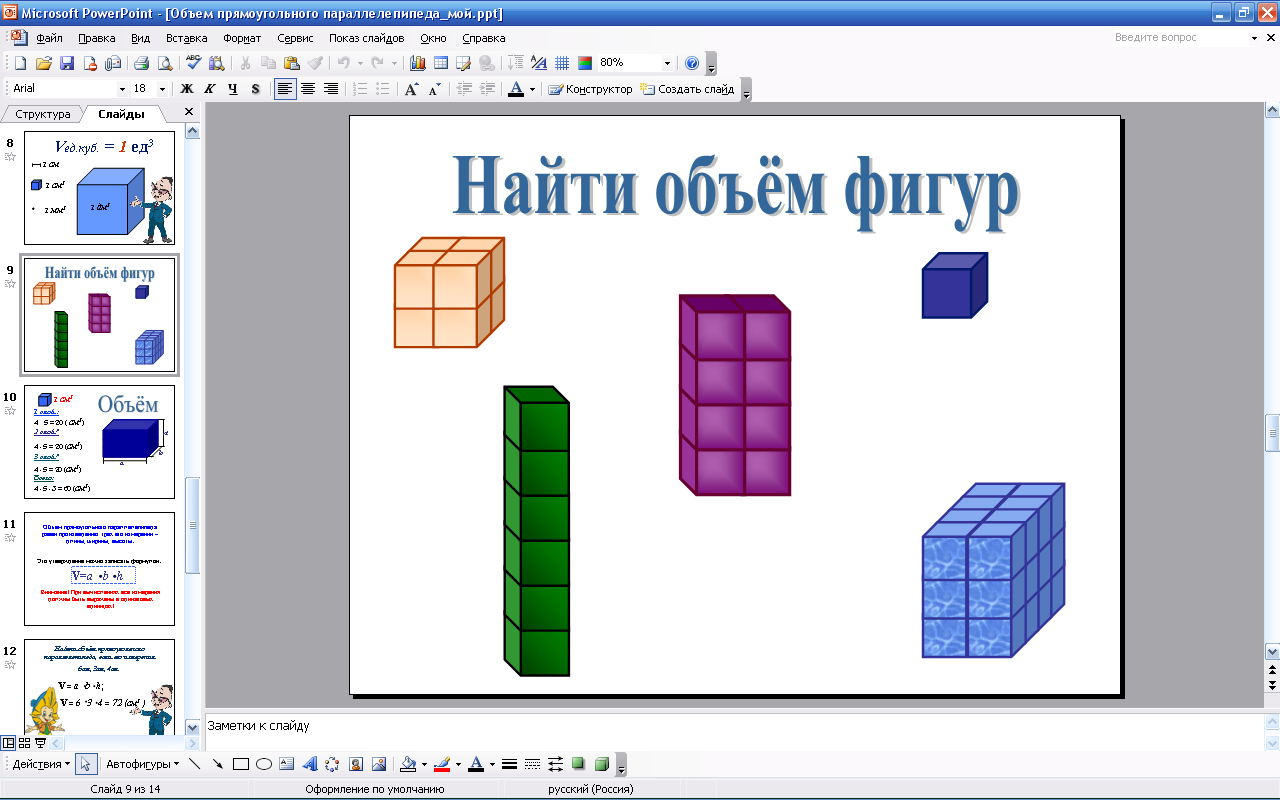

1)V=1

2)V=6

3)V=8

4)V=8

5)V=24

Возьмём за единичный куб – куб с ребром 1 см. Его объём будет равен 1 см³. Найдём объём изображённого параллелепипеда.

Слайд № 10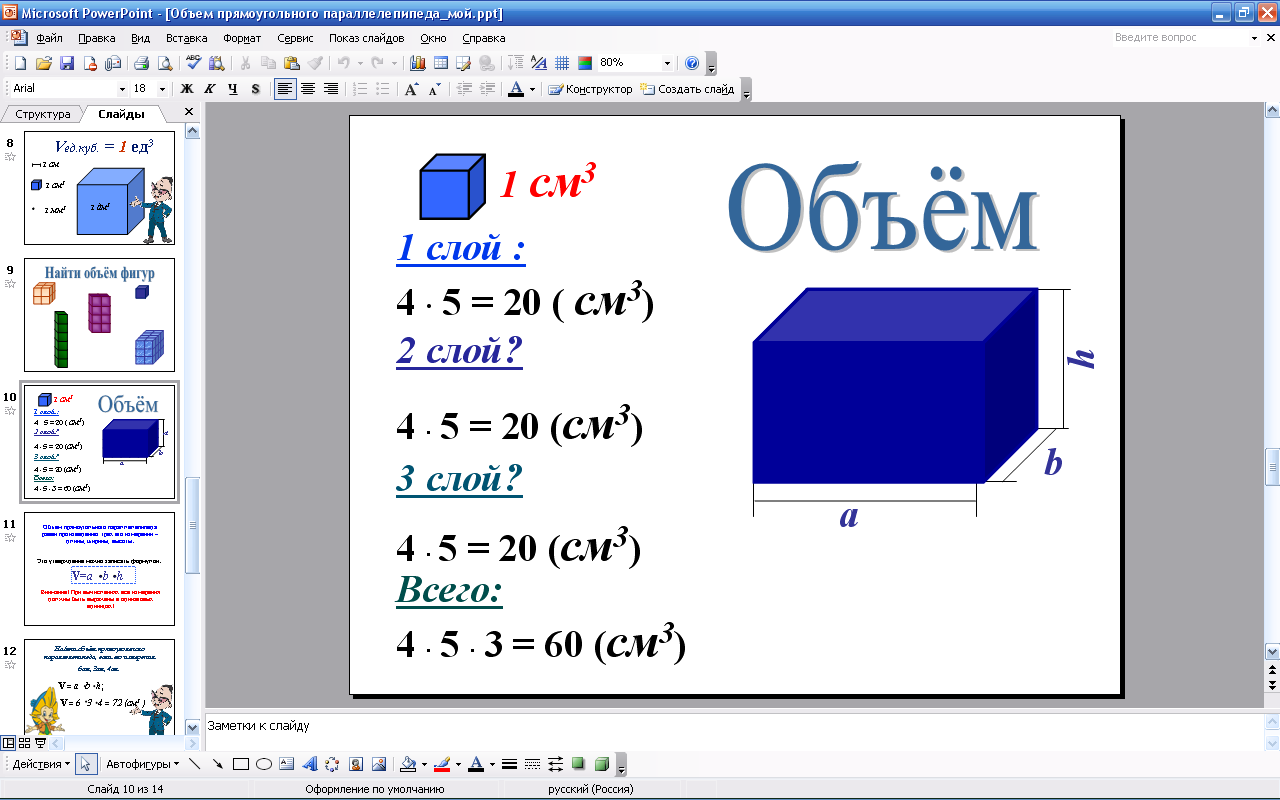

Если три измерения прямоугольного параллелепипеда – длина, ширина и высота – измерены одной линейной единицей и выражены натуральными числами a, b и c, то

объём прямоугольного параллелепипеда равен произведению трёх его измерений:

С

V = a∙b∙c

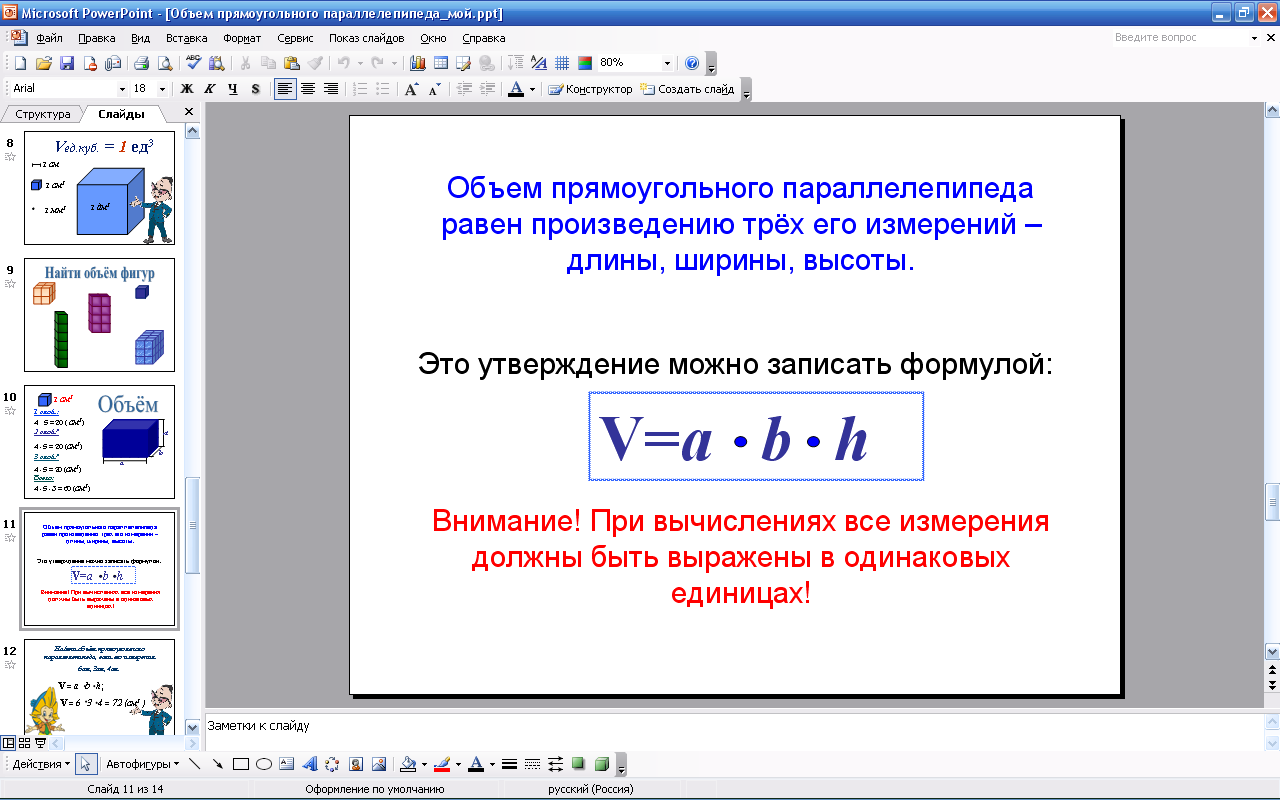Найти объём прямоугольного параллелепипеда, если его измерения 6 см, 3 см, 4 см.

Слайд № 12

Выразим одни единицы измерения объёма через другие.

Слайд № 13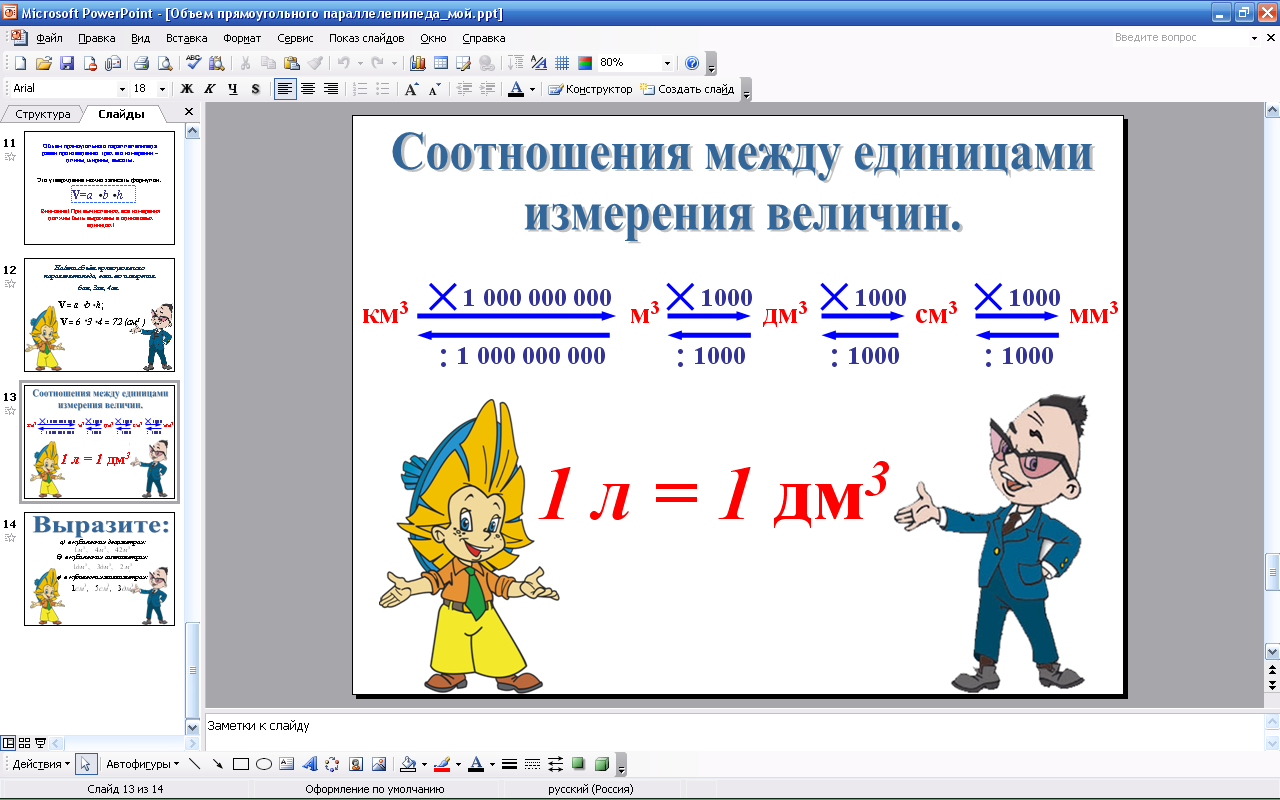

1 см³=10∙10∙10 мм³=1000 мм³

1 дм³=10∙10∙10 см³=1000 см³

1 м³=10∙10∙10 дм³=1000 дм³

1 км³=1000∙1000∙1000 м³=

=1000000000м³= 10⁹ м³

Для измерения объёмов жидкостей и сыпучих веществ используют специальную меру – литр (обозначают 1л):

1 л=1 дм³

С лайд № 14

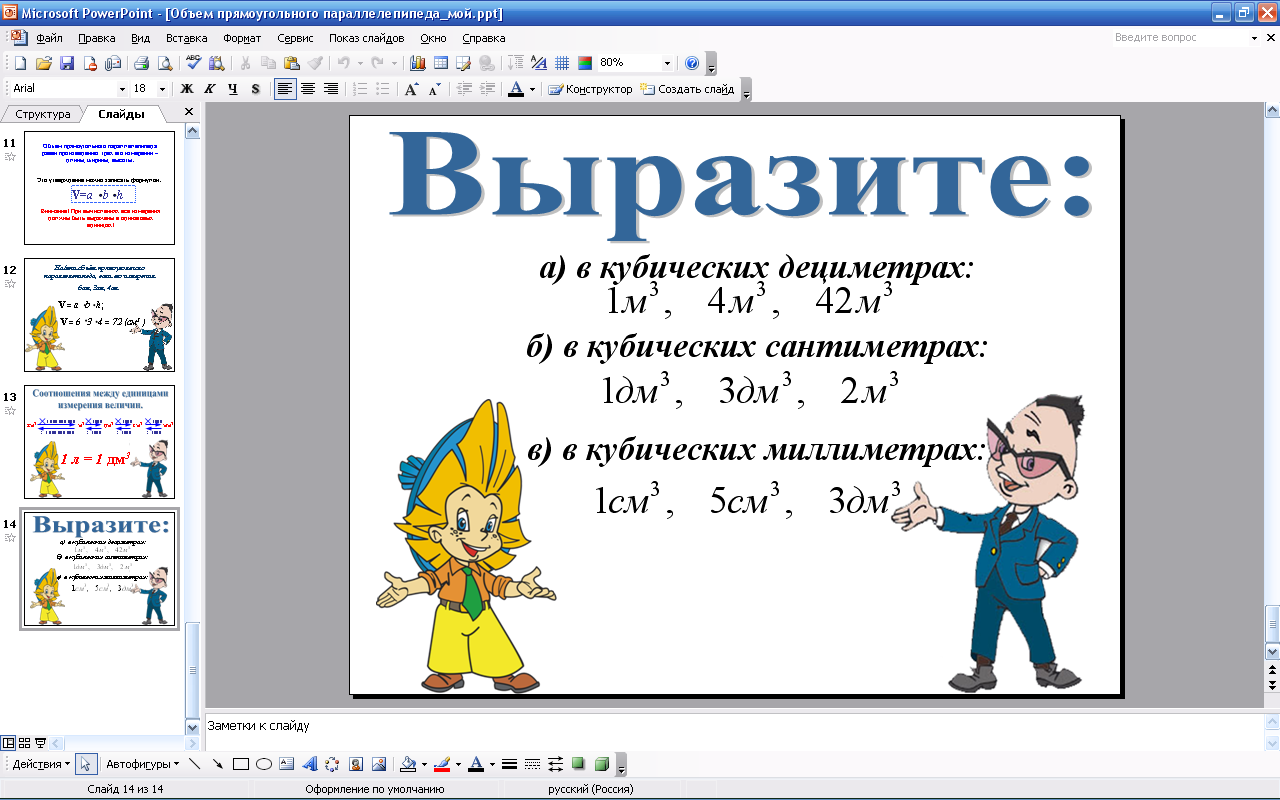Давайте выразим одни единицы измерения объёма через другие.

.

Это квадрат, сторона которого равна одной линейной единице.

Е диничный куб – это куб, длина ребра которого равна одной линейной единице

V_{ед.куба} = 1 ед³

1 мм³, 1 см³, 1 м³, 1 км³

С помощью единичных квадратов измеряют площадь прямоугольников. Сколько единичных квадратиков вмещается в прямоугольник, такова его площадь.

И змерить объём прямоугольного параллелепипеда – значит подсчитать, сколько в нём содержится единичных кубов.

1)V=1

2)V=6

3)V=8

4)V=8

5)V=24

V = a∙b∙c

(кубических единиц)

V=a∙b∙c

V=6 3 4 = 72 (см3)

1 см³=10∙10∙10 мм³=1000 мм³

1 дм³=10∙10∙10 см³=1000 см³

1 м³=10∙10∙10 дм³=1000 дм³

1 км³=1000∙1000∙1000 м³=

=1000000000м³= 10⁹ м³

1 л=1 дм³

а) 1м³=1000дм³, 4м³=4000дм³, 42м³=42000дм³

б) 1дм³=1000см³, 3дм³=3000см³, 2м³=2000000см³

в) 1см³=1000мм³, 5см³=5000мм³, 3дм³=3000000мм³

5. Домашнее задание

Молодцы. Запишите домашнее задание.

Параграф 20, 21. Прямоугольный параллелепипед. Объём прямоугольного параллелепипеда.

Номера № 815, № 843,

№ 844, №846(а)

.

Записывают домашнее задание в дневники.

5. Подведение итогов

Сегодня на уроке мы с вами узнали, что можно измерить объём фигур.

Давайте же с вами вспомним единицы измерения объёма.

Ещё мы с вами узнали формулы для нахождения объёма прямоугольного параллелепипеда, если известны три его измерения.

Верно. Молодцы. Спасибо. Урок окончен.

1 мм³, 1 см³, 1 м³, 1 км³

V = a∙b∙c