Объём прямой призмы и цилиндра

12/2/18

ОБЪЕМ ПРЯМОЙ ПРИЗМЫ

Рассмотрим два равных многоугольника А1А2…Аn и В1В2…Bn, расположенные в параллельных плоскостях α и , так что отрезки А1В1, А2В2, …, AnBn, соединяющие соответственные вершины многоугольников параллельны. Каждый из n четырех-угольников А1А2В2В1, …, AnA1B1Bn - параллелограмм.

(Почему?)

Многогранник, составленный из двух равных многоугольников А1А2…Аn и В1В2…Bn, расположенных в параллельных плоскостях, и n параллелограммов, называется призмой .

ПРИЗМА

Призму с основаниями A1A2…An и В1В2…Вn обозначают A1A2…AnВ1В2…Вn и называют

n-угольной призмой.

Четырехугольная призма

Треугольная призма

Шестиугольная призма

Высота призмы – это перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания.

Если боковые ребра призмы перпендикулярны к основаниям, то призма называется прямой , в противном случае – наклонной. Высота прямой призмы равна ее боковому ребру.

Прямая призма

Наклонная призма.

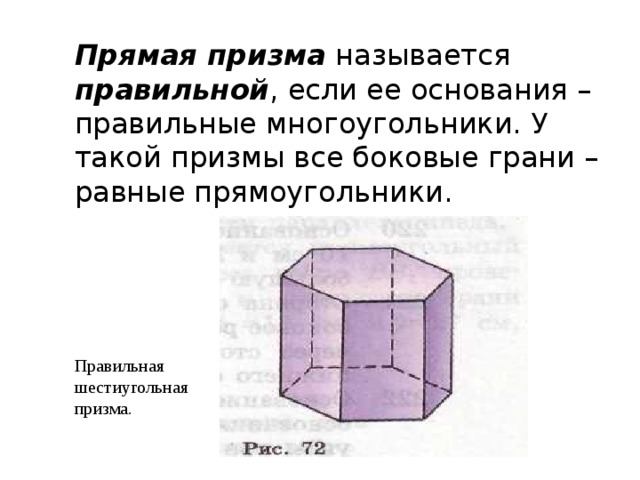
Прямая призма называется правильной , если ее основания – правильные многоугольники. У такой призмы все боковые грани – равные прямоугольники.

ПОЧЕМУ?

Правильная шестиугольная призма.

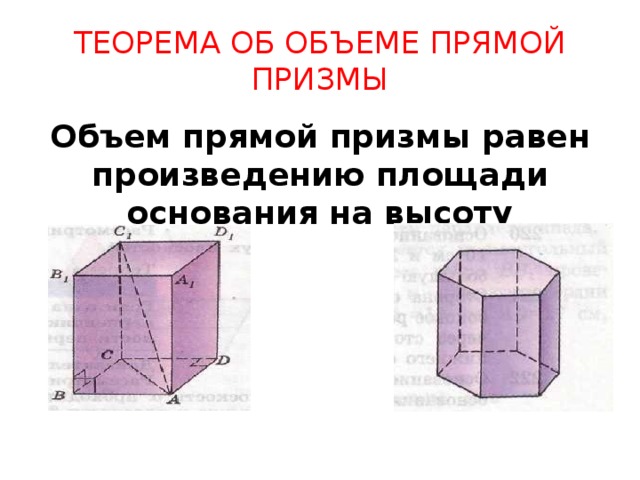
ТЕОРЕМА ОБ ОБЪЕМЕ ПРЯМОЙ ПРИЗМЫ

Объем прямой призмы равен произведению площади основания на высоту

Таблица вычисления площадей основания

Правильная призма

S осн

Треугольная призма

Четырехугольная призма

Шестиугольная призма

а 2

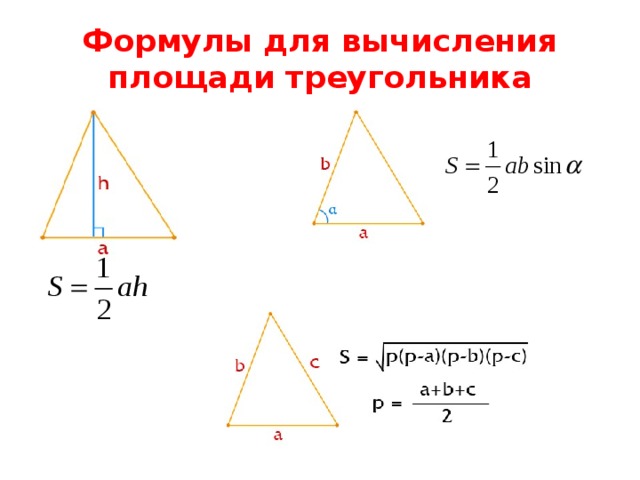
Формулы для вычисления площади треугольника

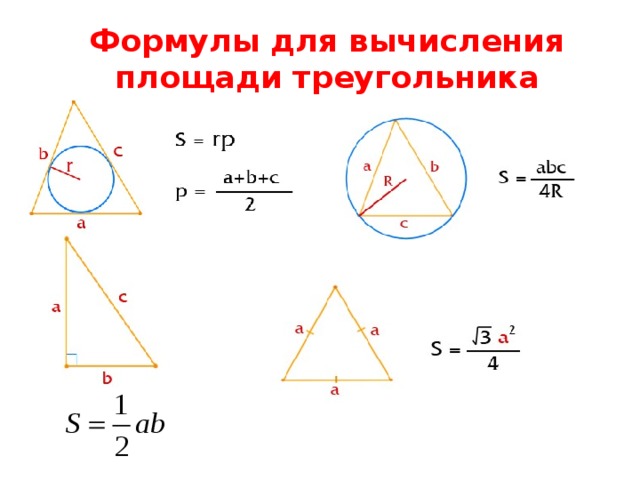
Формулы для вычисления площади треугольника

Решение задач

№ 659 (а)

660

663

664

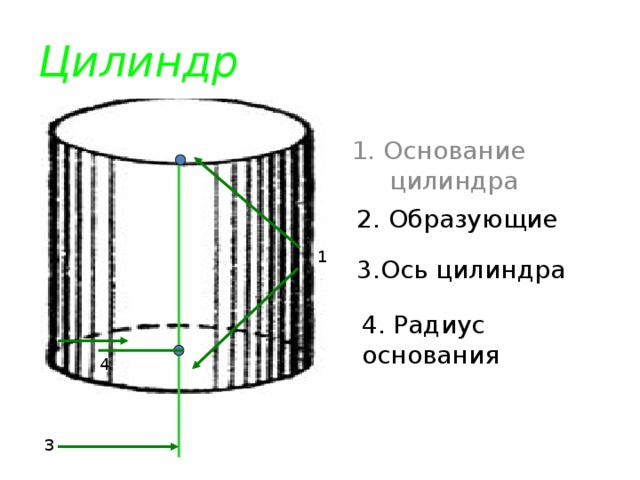
Цилиндр

1. Основание цилиндра

2. Образующие

1

3.Ось цилиндра

4. Радиус основания

2

4

3

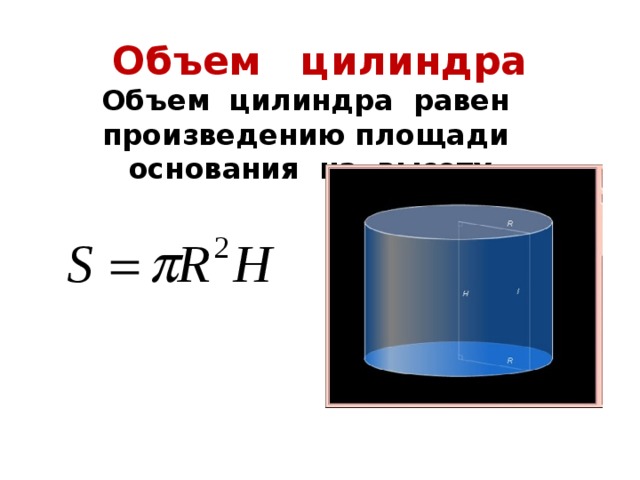
Объем цилиндра

Объем цилиндра равен произведению площади основания на высоту

Решение задач

666 (а, в)

668

669

670

Домашнее задание

659 (б)

665

666 (б)

667