Обобщение педагогического опыта по теме "«Проектная деятельность учащихся на уроках математики, как средство формирования ключевых компетенций».

Обобщение педагогического опыта.
"Элементы исследовательской деятельности на уроках математики "

учителя математики МОУ СОШ№16 г.Орехово-Зуево Московской области Минаевой Татьяны Михайловнвы

«Если человек в школе не научится творить, то и в жизни он будет только подражать и копировать».

Л.Н.Толстой.

• Концепция модернизации российского образования определила новую стратегию образования, ориентированную на развитие личности и формирование ключевых компетенций.

• Реалии нашей жизни таковы, что востребованными оказываются люди, способные активно откликаться на возникающие перед обществом проблемы, умеющие системно мыслить, анализировать, сравнивать,  делать выводы, а также практически решать возникающее перед ними жизненные и профессиональные проблемы.

• Меняющийся мир предъявляет новые требования к выпускнику общеобразовательной школы.

Возникает проблема: что должен делать учитель для формирования у школьника компетенций в конкретном предметном поле?

Какие методы, приёмы, технологии необходимо использовать для того чтобы:

• научить школьников приобретать самостоятельно недостающие знания из разных источников;

• научить пользоваться приобретенными знаниями для решения познавательных и практических задач;

• приобрести коммуникативные умения, работая в различных группах;

• развить исследовательские умения.

Метод проектов является одной из тех технологией,  которая способна решить задачи «новой школы».

Проектная деятельность – это важнейшая компетенция, на которую нацелено проектное обучение.

• В основе проектного обучения лежит «метод проектов».

• В основу «метода проектов» положена идея о направленности учебно-познавательной деятельности школьников на результат, который получается при решении той или иной практически или теоретически значимой проблемы.

Преимущества проектно- исследовательского метода это:

Творческое и личностное развитие ученика. Возможность самореализации.

У учащихся повышается интерес к получению знаний, растет уверенность в своих силах, развиваются способности к самообразованию, Появляется возможность развивать мышление, память, а так же коммуникабельность, креативность, что находит отражение в современной жизни. Задачи образования превосходят по своему уровню задачи, выдвигаемые другими методами. Профессионально-квалификационный рост учителя- исследователя. Повышение статуса ученика, учителя и учебного заведения

Исследовательский метод обучения применим на всех ступенях обучения — с учетом возрастных возможностей и подготовки учащихся. Этот метод применяется в трех направлениях:

- включение элемента поиска во все задания учащихся;

- раскрытие учителем познавательного процесса, осуществляемого учащимися при доказательстве того или иного положения;

- организация целостного исследования, осуществляемого учащимися самостоятельно, но под руководством и наблюдением учителя (доклады, сообщения, проекты, основанные на самостоятельном поиске, анализе, обобщении фактов).

При использовании исследовательского метода меняется роль учителя: из носителя знаний и информации учитель превращается в организатора деятельности, консультанта и коллегу по решению проблемы. Педагог выступает как организатор формы и условий исследовательской деятельности, благодаря которым у ученика формируется внутренняя мотивация подходить к любой возникающей перед ним научной или жизненной проблеме с исследовательской, творческой позиции. Учитель, как организатор учебного процесса, должен проявлять и управленческие способности, и творческий подход. Непосредственное же руководство учебно-исследовательской работой школьника — это тот вид педагогического взаимодействия, в котором максимально раскрываются возможности сотрудничества, соавторства, сотворчества.

Поэтому я считаю, что постоянное в определенной системе осуществляемое включение элементов исследовательской работы в систему прежних знаний, может обеспечить достаточно высокое качество усвоения предмета. В связи с этим моя педагогическая идея сводится к необходимости систематического применения в той или иной форме элементов исследовательской деятельности учащихся на уроках математики при органическом их сочетании с основным содержанием урока.

Теоретическая база опыта.

Метод проектов возник еще в 20-е годы прошлого века в США. Его называли также методом проблем. Он основывался на идеях прагматической педагогики американского философа и педагога Джона Дьюи. Его ученик и последователь В.Килпатрик, определяя суть этого метода, называл его «от души выполняемый замысел». В России метод проектов был известен еще в 1905 году. После революции метод проектов применялся в школах по личному распоряжению Н.К. Крупской. С 1919 года под руководством выдающегося русского педагога С.Т.Шацкого в Москве работала Первая опытная станция по народному образованию. В 1931 г. постановлением ЦК ВКП (б) этот метод был осужден как чуждый советской школе и не использовался вплоть до конца 80-х годов ХХ века. Идеи исследовательского метода обучения получили развитие в трудах ученых Б.П. Есипова, М.А. Данилова, М.Н. Скаткина, И.Я. Лернера. Они указывали, что главным смыслом исследования в сфере образования является то, что оно является учебным. Это означает, что его главной целью является развитие личности, а не получение объективно нового результата, как в «большой» науке.

Исследовательская деятельность учащихся – это совокупность действий поискового характера, ведущая к открытию неизвестных для учащихся фактов, теоретических знаний и способов деятельности.

Цель исследовательского метода – «вызвать» в уме ученика тот самый мыслительный процесс, который переживает творец и изобретатель данного открытия или изобретения. Школьник должен почувствовать прелесть открытия.

Таким образом, исследовательский процесс – это не только логико-мыслительное, он и чувственно-эмоциональное освоение знаний.

Метод проектов всегда ориентирован на самостоятельную деятельность учащихся – индивидуальную, парную, групповую, которую учащиеся выполняют в течение определённого отрезка времени. Метод проектов всегда предполагает решение какой-то проблемы. Метод проектов как педагогическая технология предполагает совокупность исследовательских, поисковых, проблемных методов, творческих по своей сути.

Основные компоненты проектной деятельности учащихся.

Можно обозначить основные компоненты проектной деятельности учащихся как дидактического метода:

- наличие социально значимой задачи (проблемы) – исследовательской, информационной, практической (работа над проектом – это разрешение данной проблемы);

- реализация первого этапа работы над проектом как планирования действий по разрешению проблемы, иными словами – проектирования самого проекта;

- обязательное присутствие деятельности по поиску информации, которая затем будет обработана, осмыслена и представлена участниками проектной группы;

- наличие значимого продукта (выхода проекта) как результата работы над проектом;

- представление (презентация) продукта и его социальной значимости на последнем этапе работы над проектом.

То есть проект – это «пять П »:

Проблема – Проектирование (планирование) – Поиск информации – Продукт – Презентация.

Шестое «П» проекта – его Портфолио, т.е. папка, в которой собраны все рабочие материалы проекта. Среди них черновики, дневные планы, отчёты.

Классификация проектов

• Проект может быть групповым и персональным.

• По доминирующей деятельности учащихся: исследовательские; творческие; ролевые (игровые); ознакомительно-ориентировочные (информационные); практико-ориентированные (прикладные).

• По комплексности проекты могут быть монопроектами ( в рамках одного предмета, одной области знаний) и межпредметными( в разных областях) .

• По характеру контактов проекты бывают: внутриклассными, внутришкольными, региональными и международными.

• По продолжительности различают: минипроекты

( укладываются в один урок или даже его часть);

краткосрочные (на 4-6 уроков); недельные;

долгосрочные проекты ( как индивидуальные, так и групповые; выполняются, как правило, во внеурочное время).

Виды исследовательской деятельности учащихся на уроках математики: Исследовательский подход к введению математических понятий. Исследовательские работы (мини-проекты), проводимые на уроках математики.

Исследовательские задачи.

Основные этапы работы над проектом.

Этапы работы	Содержание этапа	Деятельность учащихся	Деятельность учителя
Погружение в проект (подготовительный этап)	Мотивация, постановка проблемы, выбор темы проекта, определение его цели и задачи	Коллективное обсуждение предложенной для изучения информации целеполагания, выбор вида и способа деятельности для достижения поставленной цели, создание проектных групп	Постановка проблемы, мотивация и объяснение цели проекта, оказание помощи в создании проектных групп.
Планирование работы	Отбор источников информации и выбора способов представления конечного результата деятельности	Планирование деятельности, определение сроков, выбор формы представления результатов и распределение обязанностей в каждой группе (в зависимости от выбранной индивидуальной темы исследования)	Необходимая консультационная и организационная помощь.
Поисково-информационная деятельность	Работа с источниками информации: анализ и обобщение полученных сведений	Поиск, отбор и изучение необходимой информации в научной литературе и сети Интернет. Проведение исследования, выполнение практических заданий.	Помощь в текущей поисковой, аналитической и практической работе. Организация консультаций. Наблюдение.
Результаты и выводы	Анализ полученных результатов с позиции выдвигаемой гипотезы, формулирование выводов	Анализ и синтез найденной информации, формулирование выводов. Консультация с учителями -предметниками. Оформление результатов, подготовка материалов для защиты проекта, создание презентации	Консультационная и методическая помощь в подготовке презентации. Организация консультаций с учителями-предметниками.
Презентация (защита проекта)	Открытый отчет участников проекта о проделанной работе	Демонстрация результатов проделанной работы каждой проектной группой в форме принятой в ходе проектирования	Участие в обсуждении
Оценка процессов и результатов работы	Оценка конечного результата коллективной деятельности. Анализ и обобщение результатов работы в целом	Оценка участниками групп индивидуального вклада каждого члена в реализацию проекта, а также всей группы. Самооценка реализации поставленных целей	Участие в коллективном анализе и оценке результатов

Технология опыта.

В качестве основного средства организации исследовательской работы выступает система исследовательских заданий.

Исследовательские задания – это предъявляемые учащимся задания, содержащие проблему; решение ее требует проведения теоретического анализа, применения одного или нескольких методов научного исследования, с помощью которых учащиеся открывают ранее неизвестное для них знание.

Примеры задач исследовательского характера

Задача 1. Может ли корень уравнения 3(х ─ 4) ─ b = х ─ 11 являться положительным числом? При каком условии?

Задача 2. Верно ли, что при любом значении k система уравнений х 2 + у2 = 9, х ─ у = k. имеет единственное решение?

Задача 3. Могут ли не пересекаться графики функций у = ах2 + 3х ─ 4 и у = ах ─ 5?

Задача 4. Могут ли числа а, в, с быть одновременно последовательными членами арифметической и геометрической прогрессий?

Задача 5. Имеет ли решение уравнение (х + 6) + (х + 9) + (х + 12) + (х + 15) + (х + 18) + (х + 21) + (х + 24) = 182 ?

Задача 6. Существуют ли такие значения а, что уравнение (а2 + а ─ 2) х = а ─ 1 не имеет корней?

Задача 7. Найти значения параметра m, при каждом из которых уравнение 2x2 + 3x + m = 0 имеет два различных отрицательных корня.

Задача 8. Углом какой четверти является угол α, если sinα · cosα · tgα · ctgα 0?

Задача 9. Найдите наименьшее значение функции g(x)=log3 (16-x 2 ) на промежутке [0;√7].

Общая схема последовательности проведения исследований школьниками:

- выделение и постановка проблемы (выбор темы исследования);

- выработка гипотез;

- поиск и предложение возможных вариантов решения;

- сбор материала, анализ и обобщение полученных данных;

- подготовка и защита итогового продукта (сообщение, доклад, макет).

Овладение проектированием должно происходить не только при осуществлении целостного проекта, но и при включении в канву традиционного урока элементов проектной деятельности или какой-нибудь части проекта.

Например , можно провести мини-исследование на уроке геометрии при изучении темы «Равнобедренная трапеция» .

Назвать основные элементы трапеции: стороны, углы, диагонали. Сегодня мы изучим этот четырехугольник. Что интересует геометров при изучении фигур в первую очередь? (Соотношения между сторонами и углами).

Какова цель нашего исследования? (Выявить соотношения между элементами трапеции, изучить другие особенности этой фигуры).

Возьмите инструменты, измерьте стороны, углы, диагонали. Сформулируйте гипотезы о свойствах этих элементов.

Сформулируем другие особенности трапеции. (Высоты, проведенные из вершин меньшего основания, отсекают от нее равные прямоугольные треугольники) (Диагонали разбивают трапецию на два равных и два равнобедренных треугольника) .

Можно ли считать, что мы изучили фигуру? Нет. У нас только гипотезы.

Сформулируем и докажем теоремы . «В трапеции с равными боковыми сторонами углы при основании равны, диагонали равны, высоты, проведенные из вершин меньшего основания, отсекают от нее равные прямоугольные треугольники.»

Применение понятия

Задача 1. В равнобедренной трапеции основания равны 4 и 6 диагональ равна √73. Найти боковую сторону.

Задача 2. В равнобедренной трапеции с углом 600, разность оснований равна 5 см. Найти боковую сторону трапеции.

Задача 3. Диагонали равнобедренной трапеции перпендикулярны и равны12√2 , а ее меньшее основание 5 см. Найти большее основание трапеции.

Исследование зависимости площади прямоугольника от длин сторон.

Периметр прямоугольника 24 см, а его основание х см. Задайте формулой зависимость площади S от x. Заполните таблицу:

Х м	2	3	4	5	5,5	5,8	6	6,2	6,5	6,8	7	8	9
S

При каком значении x получился прямоугольник наибольшей площади S; каково наибольшее значение S;

выбрать два значения x и вычислить S;

удалось ли получить значение S, большее, чем ранее?

какую гипотезу можно высказать о форме прямоугольника наибольшей S, имеющего данный периметр.

Исследование зависимости между отрезками пересекающихся хорд Построить окружность радиуса 50 мм. Отметить точку K на расстояние 40 мм от центра. Обозначив длину одного из отрезков хорды, проходящей через точку K, через x (мм), а другого – y (мм), построить хорды, для которых в таблице указано значение:

x	10	12	16	20	24	26	28	30	32	36
y

вычислите произведение xy в каждом случае;

есть ли какая-нибудь закономерность?

сформулируйте гипотезу;

какую длину имеет наименьшая из хорд?

каковы длины отрезков этой хорды?

постройте график зависимости y(x).

Исследование зависимости времени движения от маршрута.

Из пункта А в пункт В можно попасть, проехав 10 км по шоссе до пункта В1 , а затем 4 км по грунтовой дороге В1В. По шоссе скорость движение равна 15м/с, по дороге 12 м/с, а по целине 10 м/с. Сколько времени потребуется вездеходу на путь АВ по маршруту АВ1В?

Может ли вездеход быстрее достичь пункта В, если свернет на целину? Заполнить таблицу зависимости времени движения t(сек) вездехода от расстояния x(м) от точки С, в которой вездеход сворачивает с шоссе, до точки В1 .

x	1000	2000	3000	4000	5000	6000	7000
t

Найти с точностью до 100 м, на каком расстоянии от В1 , должен свернуть с шоссе вездеход, чтобы время, затраченное на путь АВ, было наименьшим.

Проекты в учебной деятельности

Класс	Вид проектов	Примеры проектов	Роль педагога
5	Введение элементов: Постановка проблемы Выдвижение гипотезы	«Решение уравнений» «Задачи на проценты в жизни человека» «Действия с десятичными дробями»	Руководитель
6	Мини-проекты	«Делимость чисел» «Нахождение дроби от числа»	Консультант
7-9	Групповые проекты, индивидуальные проекты	«Методы решения систем уравнения с двумя неизвестными» «Тела вращения»	Координатор

Проекты во внеурочной деятельности

В рамках внеурочной деятельности проектная деятельность направлена на обогащение содержания образования и возможность реализации способностей, потребностей и интересов обучающихся с различным уровнем развития.

Вид деятельности	Классы	Виды проектов	Примеры
Курс: «Занимательная математика»	5-6	Мини-проекты проекты Групповые проекты	«Числа великаны» «Из истории арифметических действий» «Старинные задачи»
Подготовка к олимпиадам: «Кенгуру», «Олимпус», «Математика и я» и т.д.	5-6	Мини-проекты Групповые проекты Долгосрочные проекты	«Математические ребусы» «Нестандартные задачи и их решение»

Проектный метод в математике формирует следующие компетенции:

• Мыследеятельностные: выдвижение идеи (мозговой штурм); проблематизация; целеполагание и формулирование задачи; поиск гипотезы; выбор способа или метода; самоанализ и рефлексия.

• Презентационные: построение устного доклада (сообщения) о проделанной работе; выбор способов и форм наглядной презентации; изготовление предметов наглядности; подготовка письменного отчёта( продукта) о проделанной работе.

• Коммуникативные: слушать и понимать других; выражать себя; находить компромисс; взаимодействовать внутри группы.

Исследовательская работа с учащимися способствует:

-развитию предпрофессиональных навыков

-воспитанию культуры и индивидуальности личности учащегося

-формированию исследовательской компетенции

-развитию творческих способностей учащихся

Развитие исследовательских умений дает:

возможность освоения методов исследования и использование их при изучении материалов любых дисциплин;

возможность применения полученных знаний и умений в реализации собственных интересов, что способствует дальнейшему самоопределению учащихся;

возможность развития интереса к различным наукам, школьным дисциплинам и процессам познания в целом.

Исследовательскую деятельность можно организовать на трех уровнях: школьном, учебно-исследовательском и научно-исследовательском.

Первый уровень позволяет привлечь достаточное количество учащихся, но тематика при этом довольно простая (отвечающая интересам автора работы), а работа представляет собой просто поиск информации по первоисточникам.

Второй уровень обязательно требует помимо умения работать с первоисточниками также проведения экспериментов, накопления данных для построения таблиц, графиков, диаграмм.

Третий уровень требует не только практической значимости выбранной темы, но и новизны в ее разработке, т.е. своих логических умозаключений, собственных предложений по проведению эксперимента, трактовке его результатов и т.п.

Исследовательская деятельность позволяет учащимся выйти в культурное пространство самоопределения. Учащийся оказывается в ситуации проектирования собственной деятельности, сталкивается с необходимостью анализа последствий своей деятельности. Каждый достигнутый им результат рождает этап рефлексии, имеющий следствием появление новых замыслов и творческих планов. Исследования трудных, дискуссионных, не вполне решенных проблем пробуждают у школьников сознание серьезности их исканий.

Следующим видом исследовательской деятельности учащихся является подготовка доклада для участия в конференциях. Для участников конференций характерно наличие следующих качеств: развитие познавательных, эвристических способностей школьника, углубленное знание по предмету, развитие умений решать нестандартные задачи и задачи повышенной сложности за пределами школьной программы, а так же творческих качеств исследователя. Школьники – участники конференций – уже не просто решают учебные или олимпиадные задачи, они выполняют реальное научное исследование в той или иной области науки, техники, искусства. Для того чтобы принять участие в научно – практической конференции, необходимо заниматься исследовательской работой, а чтобы успешно выступить на ней, надо провести серьезное научное исследование: определить цели и задачи, объект и предмет исследования, изучить большое количество литературы, выдвинуть гипотезу, провести, используя разные методы, само исследование, получить результаты, сделать выводы, оформить работу.

Одной из наиболее рациональных форм организации исследовательской деятельности является работа учащихся в парах. Следует отметить, что в этом случае качество работы, уровень подготовки и результативность резко повышаются, т.к. учащиеся неоднократно обсуждают свою тему, советуются, спорят, взаимно проверяют выученный материал, исправляют ошибки и недочеты.

Эффективность исследовательской деятельности зависит от меры увлеченности ученика этой деятельностью, от умения ее выполнять.

Анализ результативности.

На уроках математики при решении практически любой задачи проводится так называемое мини-исследование, где используются основные мыслительные операции - анализ и синтез, индукция и дедукция, сравнение и аналогия, обобщение и конкретизация;

-при решении задач различными способами

-при решении задач с параметрами также используется исследовательская деятельность: ставится вопрос о существовании решения, о числе решений, об особых случаях, какие могут представиться в зависимости от значения параметра.

При применении исследовательского метода в учебном процессе учитель  не дает готовых знаний, он организует самостоятельную, творческую, поисковую  деятельность обучающихся, которые самостоятельно решают новые для них познавательные задачи или находят в известных для них задачах, теоремах новые способы решения или доказательства. Только в процессе такой деятельности можно развить творческие способности ребенка.

Практика моей работы по использованию исследовательской деятельности учащихся на уроках математики показала, что исследовательский метод позволяет активизировать мыслительную деятельность учащихся, повысить их интерес, и приводит к хорошему усвоению материала, к развитию мышления и способностей учащихся. Результатом моей работы по применению данной технологии можно считать победы и призовые места в школьных, муниципальных олимпиадах по математике, призовое место в районных математических чтениях учащихся, посвященных 220-летию со дня рождения русского ученого математика Н.И. Лобачевского, два первых места в районных математических чтениях, посвященных 110-летию со дня рождения А.Н. Колмогорова, участие в ежегоной районной научно-практичекой конференции « Шаг в будущее» Петушинский район с работами : « Проценты в нашей жизни», «Математика и литература», «Информационное общество- миф или реальность?», получение Золотых и Серебряных медалей моими выпускниками по окончании школы.

Трудности и проблемы при использовании данного опыта.

В то же время этому методу присущи следующие трудности и проблемы:

- он требует большей, чем при сообщении готовых знаний, затраты времени;

- при этом методе особенно сильно сказываются индивидуальные различия учащихся: многие из них не успевают решать поставленные проблемы, отвечать на вопросы учителя. А учитель на уроке не имеет возможности ждать, пока все самостоятельно придут к нужному выводу;

- активное участие в решении проблемы или в беседе принимают лишь отдельные учащиеся, остальные – пассивны.

Поэтому исследовательский метод следует использовать в разумной мере, нейтрализуя его недостатки с помощью различных приёмов. Прежде всего нужно помочь тем учащимся, которые не успевают решать на уроках поставленной проблемы.

На уроке ставятся нетрудоёмкие проблемы, которые успевают решить все учащиеся класса с небольшой разницей во времени. Более трудоёмкие проблемы можно включать в домашние задания. В этом случае на уроке только создаётся проблемная ситуация и ставится проблема. Тогда в домашних условиях каждый ученик может спокойно, не торопясь, рассмотреть достаточное число частных случаев, обратиться к книгам и самостоятельно прийти к «открытию».

Уроки с применением исследовательского метода более интересны и познавательны для учащихся.

Опыт моей работы может быть использован учителями при работе над исследовательским методом в преподавании математики в 5-11 классах и во внеурочной деятельности.

Программа факультативного курса

«Математика очевидная и невероятная»

7-9 класс

(естественно-научная линия)

Класс 7-9

Автор программы Минаева Татьяна Михайловна, учитель

математики высшей квалификационной

категории.

Количество часов 34 часа

Срок реализации 1 год

Г .Петушки 2015 год

ПОЯСНИТЕЛЬНАЯ ЗАПИСКА

Программа факультативного курса «Математика очевидная, невероятная» направлена на формирование совокупности УУД «универсальных учебных действий», которые обеспечивают возможность каждому ученику самостоятельно осуществлять деятельность учения.

Применение проектной и исследовательских технологий во внеурочной деятельности, формирует у учащихся умения анализировать, сравнивать, обобщать, учащиеся учатся работать с разными источниками информации, т.е. формируются определенные умения, составляющие основу любой, в т. ч. и проектной деятельности. Использование технологии дистанционного обучения эффективно в общении с учащимися в процессе работы над проектом, исследовательской работы При этом удается значительно повысить интерес к предмету даже у слабых учеников, включить их в процесс познания.

Курс носит обобщающий характер, направлен на закрепление умений и навыков, полученных в 7-9 классах средней школы. А также на расширение и углубление теоретических знаний по математике.

Содержание курса предполагает научить учащихся искать, отбирать и изучать учебную информацию, размещенную в Интернете, формировать нестандартное мышление и математическую зоркость, нацелен на ознакомление учеников с социальными сервисами и умение использовать их в контексте приобретенных знаний.

Актуальность курса обусловлена его практической значимостью. Дети могут применить полученные знания и практический опыт при сдаче ОГЕ, а в дальнейшем –ЕГЭ

Весь дистанционный курс условно разбит на 5 основных тем, каждая из которых состоит из лекций, индивидуальных и групповых консультаций полезных ссылок для ознакомления, презентаций, тестов и тренировочных работ. Каждую тему необходимо изучить, в определенные сроки выполнить предложенные задания. После изучения темы предполагается выступление каждой группы с отчетом в виде презентации на занятиях факультатива, в блоге с последующим обсуждением. Дистанционное общение нацелено на проведение рефлексии по изучению тем и повышение мотивации к обучению.

Цель программы:

- Развитие познавательных навыков учащихся, способностей самостоятельно конструировать и использовать свои знания, умений ориентироваться в информационном пространстве и критически осмысливать полученную информацию;

-Оказзать методическую поддержку учащимся при проведении исследовательских работ и подготовке выступлений (презентаций) на факультативных занятиях и блоге с последующим, возможным выходом на научно-практическую конференцию.

Задачи программы: использование элементов дистанционного обучения во внеурочной деятельности позволяет решить задачи по формированию компетенций у школьников:

- учебно-познавательной (определять цели и порядок своей работы, самостоятельно планировать свою учебную деятельность, осуществлять самоконтроль;

-коммуникативной (сотрудничать, участвовать в работе группы, обмениваться информацией);

- информационной (самостоятельно искать, анализировать и отбирать информацию. Преобразовывать и передавать ее);

- компетенции личностного само совершенствования (анализировать свои достижения, ошибки, критически оценивать и переоценивать результаты своей деятельности.

Актуальность программы. : «… Проектное обучение поощряет и усиливает истинное учение со стороны учеников, расширяет сферу субъективности в процессе самоопределения, творчества и конкретного участия …» В. Гузеев

Ценность программы состоит в том, что применение дистанционных технологий в обучении школьников в сочетании с современными информационными технологиями дает возможность совершенствоваться учителю и создавать условия для развития своих учеников, а также выполнять основную задачу современного образования- учить ребенка учиться, помочь ему быть успешным.

Условия реализации образовательной программы:

Данная программа рассчитана на учащихся 7-9 классов, интересующихся исследовательской деятельностью. Специального отбора нет, главное - желание ребенка включиться в учебно-исследовательскую деятельность, научиться выполнять исследовательскую работу.

Вступление в состав группы возможен в любое время, но желательно в начале изучения теоретического блока.

Продолжительность реализации программы: программа рассчитана на 34 часа

( один год) и предполагает выполнение трех проектов, исследовательских работ.

Формы и режим занятий:

Режим занятий: 1 час в неделю; 2 ёраза в неделю по 0,5 ч- в режиме Онлай-консультаций. Без оценочная форма обучения.

Программа предполагает как теоретические, так и практические занятия.

Программа предусматривает использование фронтальной, индивидуальной, групповой форм работы обучающихся.

Фронтальная форма предусматривает подачу материала всему коллективу обучающихся.

Индивидуальная форма предполагает самостоятельную исследовательскую работу обучающихся. В программе отводится индивидуальной работе приоритетное место. Групповая работа позволяет ориентировать учеников на создание так называемых «творческих» пар или подгрупп с учетом их возраста и опыта исследовательской деятельности.

В процессе обучения предусматриваются следующие формы дистанционных занятий: обучения в режиме онлайн и в режиме офлайн. Обучение через интернет обладает рядом существенных преимуществ:

Гибкость – учащиеся могут получать консультации учителя, обмениваться информацией внутри группы в удобное время;

Дальнодействие – обучающиеся не ограничены расстоянием и могут общаться в независимости от места проживания;

Экономичность – значительно сокращается время работы над проектом, исследовательской работой.

Тематическое планирование

№№ пп	Темы занятий	Общее количество учебных часов	В том числе		Форма работы	Даты
			теоретических	практических
1	2	3	4	5	6	7
1	Методика работы над проектом
1.1.	Знакомство учащихся с этапами работы над проектом.	2	2		Лекция с использованием презентации, с элементами дискусии.
2	Проект «В мире отрицательных чисел»
2.1.	Разработка плана работы над Проектом.	1	1		Круглый стол. Ведущая роль отводится учителю.
2.2	Консультации в режиме Онлайн общения по собранной информации	6	6		Индивидуальная работа с участниками проекта в режиме Онлайн-общения.
2.3	Создание отчета по теме проекта (презентации)	2		2	Коллективное обсуждение проделанной работы. Результаты обсуждения презентации в контакте.
2.4	Отчет группы в виде презентации.	1		1	Самооценка участников проекта. Взаимооценка. Подведение итогов
3	Проект «Удивительный мир квадратных уравнений»
3.1	Обсуждение содержания проекта. Распределение под тем проекта между участниками группы.	2	2		Дискуссия.
3.2	Индивидуальные консультации через Интернет в системе Онлайн-общения	6	6		Консультации в форме вопрос-ответ.
3.3	Обсуждение презентации к проекту независимой группой обучающихся.	1	1		Круглый стол.
3.4	Защита проекта.	1	1		Выступление учащихся ,принимавших участие в работе над проектом. Самооценка. Взаимооценка.
4	Проект «Графы и их применение к решению задач»									0,5	0,5	Тренинг
4.1.	Теория графов	3	1	2	Лекция. Практика.
4.2.	Обсуждение вопросов для глубокого раскрытия темы проекта. Выбор руководителя проекта.	2	2		Дискуссия.
4.3	Индивидуальные консультации в режиме Онлайн- общения .	5	5		Обсуждение вопросов со всей группой обучающихся
4.4	Отчет по проектной работе.	1	1		Защита проекта. Самооценка. Взаимооценка.
4.5	Подведение итогов работы над проектами.	1		1	Круглый стол. Рефлексия.
	Итого	34	28	6

Содержание

1.МЕТОДИКА ТАБОТЫ НАД ПРОЕКТАМИ

1. ПОДГОТОВИТЕЛЬНЫЙ (определение темы и целей проекта)

2. АНАЛИТИЧЕСКИЙ Определение источников необходимой информации; определение способов сбора и анализа информации; определение способа представления результатов (формы проекта); установление процедур и критериев оценки результатов проекта; распределение задач между членами рабочей группы;
3. ПРАКТИЧЕСКИЙ Сбор и уточнение информации; выявление и обсуждение альтернатив возникающих в ходе выполнения проекта; выбор оптимального варианта хода проекта; поэтапное выполнение исследовательских задач.

Выводы: анализ информации; формулирование выводов.
4. ПРЕЗЕНТАЦИОННЫЙ. Планирование презентации и подготовка презентационных материалов. Представление (защита) проекта. Представление проекта (защита) включает в себя: демонстрацию результатов исследовательской деятельности; предложения по разрешению проблем.
5. КОНТРОЛЬНЫЙ. Оценка проекта: предполагает оценивание планирования, процесса, деятельности, отношения конечного результата, самооценку, определение уровня знания предмета и выявление успехов и неудач работы над проектом, анализ выполнения проекта, достигнутых результатов.
При добросовестной самостоятельной работе школьников над проектами на уроках удается значительно увеличить объем изучаемого материала. Меняется отношение учащихся к выполнению домашних заданий. Дети уже не боятся совершать ошибки, становятся более изобретательными в способах доказательства и решения задач. Этому способствуют задания проекта, совместная интеллектуальная деятельность учащихся и учителя.

Приложение. Презентация.

Проект «В мире отрицательных чисел»

Цель: - Формирование целостного представления об отрицательных числах;

Задачи: - Приобретение навыка работы над проектом;

- Формировать умение определять цели и порядок своей работы, самостоятельно планировать свою учебную деятельность, осуществлять самоконтроль;

-Учиться сотрудничать, участвовать в работе группы, обмениваться информацией;

- Учиться самостоятельно искать, анализировать и отбирать информацию. Преобразовывать и передавать ее;

- Вырабатывать умение анализировать свои достижения, критически оценивать и переоценивать результаты своей деятельности.

Примерный план исследования:

1.Психологический подход к изучению отрицательных чисел.

2. История возникновения отрицательных чисел.

3. Использование отрицательных чисел в географии.

4. Отрицательные числа в литературе.

5. Отрицательные числа в химии

Проект «Удивительный мир квадратных уравнений».

Цель: - Формировать целостное представление о квадратных уравнениях;

Задачи: - Рассмотреть различные способы решения уравнений, сводящихся к квадратным;

- Учиться самостоятельно искать, анализировать и отбирать информацию.

- Учиться сотрудничать, участвовать в работе группы, обмениваться информацией;

- Вырабатывать умение анализировать свои достижения, критически оценивать и переоценивать результаты своей деятельности.

Примерный план исследования:

1. Историческая справка.

2. Частные случаи решений полных квадратных уравнений.

3. Решение квадратных уравнений методами геометрической арифметики.

4. Решение квадратных уравнений с применением циркуля и линейки.

5. Виды квадратных уравнений и способы их решения знакомые из курса школьной математики.

Проект «Графы и их применение к решению задач»

Цель: Научить строить графы для решения логических задач.

Задачи: - Совершенствовать навык по анализу условия задачи;

- Научить строить граф, обосновывать выбор графа для решения текстовой задачи;

- Самостоятельно планировать свою учебную над темой работы, осуществлять самоконтроль;

- Учиться сотрудничать, оказывать помощь своим товарищам;

- Учиться анализировать свою работу в группе и работу других обучающихся.

На последнем этапе в форме круглого стола обсуждаются проблемы и затруднения, выслушиваются различные мнения, подводится общий итог проделанной работы. Сами определяют лучшего в работе над проектами.

Рефлексия.

Каждый участник проекта заполняет анкету.

№ п/п Фамилия имя участника Проекта.	Что мне понравилось в работе над проектами	Что мне удалось.	Над чем я хотел бы поработать

Как я оцениваю свою работу.

Больше всего мне понравилась работать над темой:

Оцени работу каждого участника группы:

Литература

1.Альхова З.Н., Макеева А.В. Внеклассная работа. – Саратов: «Лицей», 2002

2.Асарина Е.Ю., Фрид М.Е. Математика выводит из лабиринта. – М.: Контекст, 1997

3.Клименко Д.В. Задачи по математике для любознательных. – М.: Просвещение, 1991

4.Кубанина Л.М. Графы и их применение в решении задач. – Чебоксары: Чувашское изд-во, 1995

5.Леман И. Увлекательная математика. – М.: Знание, 1985

6.Шапиро А.Д. Зачем нужно решать задачи? Построение графиков. – М. Просвещение, 1996

7.Шустер Ф.М. Материал для внеклассной работы по математике. – Минск, 1968

8.Математика. 8-9 классы. Элективные курсы. Харламова. Волгоград, Учитель, 2007

9.Современная школа: опыт модернизации: Книга для учителя / Под общ. ред. А.П.Тряпициной. – СПб.: Изд-во РГПУ им. А.И.Герцена, 2005.

10. А.И.Савенков «Психологические основы исследовательского обучения школьников». // Фiзiка: праблемы выкладання. – 2007. № 3. С. 14–24.

11.О.Б.Даутова, О.Н.Крылова Современные педагогические технологии в профильном обучении. Учебно-методическое пособие для учителя. – СПб.: КАРО, 2006..

12.А.И.Савенков Исследовательское обучение - возможность преодолеть «образовательный предел». // Директор школы. - 2003. - № 10. - С. 35

13. А.В. Леонтович «Модель научной школы и практика организации исследовательской деятельности учащихся // Интернет-портал

14. «деятельность школьников» Исследователь. ru.

Б.В.Румянцев Обобщенная экспериментальная деятельность учащихся как метод решения исследовательских задач // Химия в школе. 2004.

№ 7.С. 62-66.

А.И.Савинков Об организации учебно-исследовательской деятельности в современном образовании // Химия в школе. 2008. № 8. С. 2-6.

А.И.Савинков Проектирование и исследование в современном образовании // Химия в школе. 2008. № 6. С. 2-7.

Ю.В.Сурин Проблемный эксперимент как одна из форм химического эксперимента // Химия в школе. 2007. № 10.С. 56-60.

Литература для учителя:

Исследовательская практика учащихся: методические рекомендации для учителей и учащихся средней школы № 89.- СПб, 2000.

Ивашедкина О.А. Исследовательская деятельность школьников как средство достижения метапредметных результатов образования // Естественно-научное образование в идеологии стандартов второго поколения

Приложение

Конспект занятия факультативного курса в 9 классе

«Графы и их применение в решении задач»

Цель:

Сформировать у учащихся способность составлять математическую модель к текстовой задачи, переходить от этой модели к ответам задачи, анализируя жизненную ситуацию.

Задачи:

Создать условия для успешного овладения понятием графа и его свойствами.

Формировать навык построения графа для ситуаций, описанных в текстовых задачах,

анализировать условия текстовой задачи, выявлять главное в тексте.

Ход занятия.

Учитель:

Для того, чтобы научиться решать задачи, надо разобраться в том, как они устроены, из каких частей они состоят, каковы инструменты, с помощью которых проводится решение задач.

Любая задача представляет собой требование или вопрос, на который надо найти ответ, опираясь и учитывая те условия, которые указаны в задаче. Потому, приступая к решению какой-либо задачи, надо её внимательно изучить, установить, в чем состоят её требования (вопросы), каковы условия, исходя из которых надо решать задачу. Результаты предварительного анализа задачи надо как-то зафиксировать, записать. Схематичная запись задачи должна быть удобна, компактна и в то же время достаточно наглядна. Первой отличительной особенностью схематичной записи задач является широкое использование в ней разного рода обозначений, символов, букв, рисунков, чертежей. Второй особенностью является то, что в ней четко выделены все условия и требования задачи, а в записи каждого условия указаны объекты и их характеристики, наконец, в схематичной записи фиксируется лишь то, что необходимо для решения задачи, все другие подробности отбрасываются. Эти положения соблюдены в графах.

Чтобы каждому ученику обеспечить возможность решать задачу с необходимыми объяснениями и в определенной последовательности, ему дается список указаний. Этот список предлагается или в готовом виде, или составляется вместе с учащимися класса. Ученики читают его и одновременно выполняют упражнение:

1. О каком процессе идет речь в задаче?

2. Какие величины характеризуют этот процесс?

3. Каким соотношением связаны эти величины?

4. Сколько различных процессов описывается в задаче?

5. Есть ли связь между элементами?

Отвечая на эти вопросы (вопросник этот висит на стенде в кабинете, записан на закладках или обложках тетрадей учащихся), ученики анализируют условие задачи, записывают его схематично. Эта схема –сетевой граф.

Вы, наверное, знаете, что есть такой город Калининград, раньше он назывался Кенигсберг. Через город протекает река Преголя. Она делится на два рукава и огибает остров. В XVIII веке в городе было семь мостов,

расположенных так, как показано на рисунке.

Рассказывают, что однажды житель города спросил у своего знакомого, сможет ли он пройти по всем мостам так, чтобы на каждом из них побывать только один раз вернуться к тому месту, откуда началась прогулка. Многие горожане заинтересовались этой задачей, однако придумать решение никто не смог. Этот вопрос привлек внимание ученых разных стран.

Разрешить проблему удалось известному математику Леонардо Эйлеру. Причем, он не только решил эти конкретную задачу, но придумал общий метод решения подобных задач. Эйлер поступил следующим образом: он «сжал» сушу в точки, а мосты «вытянул» в линии. В результате получилась фигура, изображенная на рисунке:

Такую фигуру, состоящую из точек и линий, связывающих эти точки, называют графом. Точки А, В, С, Л - называют вершинами графа, а линии, которые соединяют вершины - ребрами графа. На рисунке из вершины В, С, А выходят по 3 ребра, а из вершины А - 5 ребер. Вершины, из которых выходит нечетное число ребер, называют нечетными вершинами, вершины, из которых выходит четное количество ребер - четными.

Решая задачу про кенигсбергские мосты, Эйлер установил, в частности, свойства графа.

• Если все вершины графа четные, то можно одним росчерком (т.е. не отрывая карандаша от бумаги и не проводя дважды по одной и той же линии) начертить граф. При этом движение можно начать с любой вершины и окончить в той же вершине.

• Граф с двумя нечетными вершинами тоже можно начертить одним росчерком. Движение надо начинать от любой нечетной вершины, а заканчивать на другой нечетной вершине.

• Граф с более чем двумя нечетными вершинами невозможно начертить одним росчерком.

В задаче о семи кенигсберских мостах все четыре вершины соответствующего графа нечетные, т.е. нельзя пройти по всем мостам один раз и закончить путь там, где он был начат.

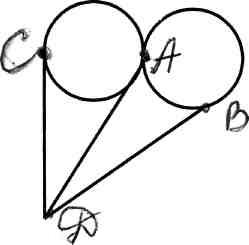
Задача.

Четыре острова соединены между собой и с берегами реки 14 мостами так, как показано на рисунке. Можно ли за одну прогулку обойти все эти мосты, побывав на каждом из них один раз? Если это возможно, то начертите один из маршрутов. Нарисуйте соответствующий граф.

Рисунок:

Имеются две нечетные вершины (В и С). Следовательно, за однку прогулку можно обойти все мосты, побывав на каждом из них один раз. При этом прогулку надо начинать с острова В и заканчивать на острове С или наоборот.

Число нечетных вершин графа всегда четное.

Если в графе имеются нечетные вершины, то наименьшее число росчерков, которое можно нарисовать граф, равно половине числа нечетных вершин этого графа.

Например, если фигура имеет четыре нечетные вершины, то ее можно начертить, самое меньшее, двумя росчеркам

Задача.

Четыре острова соединены между собой и с берегами реки 14 мостами так, как показано на рисунке. Можно ли за одну прогулку обойти все эти мосты, побывав на каждом из них один раз? Если это возможно, то начертите один из маршрутов. Нарисуйте соответствующий граф.

Рисунок:

Имеются две нечетные вершины (В и С). Следовательно, за однку прогулку можно обойти все мосты, побывав на каждом из них один раз. При этом прогулку надо начинать с острова В и заканчивать на острове С или наоборот.

Число нечетных вершин графа всегда четное.

Если в графе имеются нечетные вершины, то наименьшее число росчерков, которое можно нарисовать граф, равно половине числа нечетных вершин этого графа.

Например, если фигура имеет четыре нечетные вершины, то ее можно начертить, самое меньшее, двумя росчерками.

Граф: А

F

Задача

Мальчик нарисовал на бумаге три синих и три красных контура, которые нигде не пересекались. Затем рисунок накрыли листом бумаги так, что один из контуров оказался целиком накрыт, а все другие были частично видны. Нарисуйте закрытую часть рисунка.

Задача

В первенстве класса по настольному теннису 6 участников: Андрей, Борис, Виктор, Галина, Дмитрий и Елена. Первенство проводят по круговой системе - каждый из участников играет с каждым из остальных один раз. К кастоящему моменту некоторые игры уже проведены: Андрей сыграл с Борисом, Галиной, Еленой; Борис - с Андреем, Галиной; Виктор - с Галиной, Дмитрием, Еленой; Галина - с Андреем, Виктором и Борисом. Сколько игр проведено к настоящему моменту и сколько еще осталось?

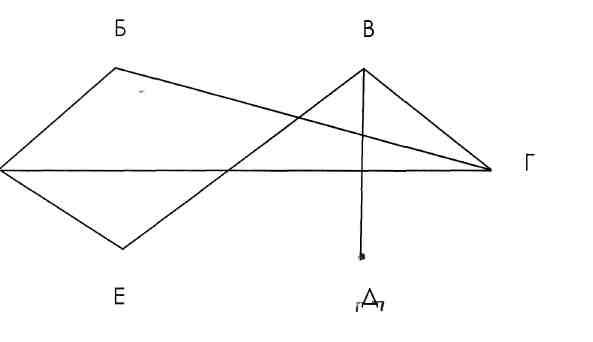
Решение:

Построим граф.

Граф

А

Сыграно 7 игр.

Граф имеет 8 ребер, следовательно, осталось провести 8 игр. Ответ: проведено 7 игр, осталось провести 8 игр.

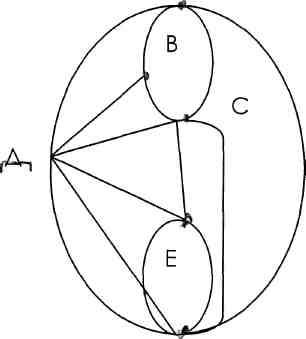
Задача

Кто играет Аяпкина-Тяпкина?

В школьном драматическом кружке решили ставить гоголевского «Ревизора». И тут разгорелся жаркий спор. Все началось с Ляпкина-Тяпкина.

-Ляпкиным-Тяпкиным буду я!- решительно заявил Дима.- С раннего детства я мечтал воплотить этот образ на сцене.

- Ну хорошо, согласен уступить эту роль, если мне дадут сыграть
Хлестакова, - проявил великодушие Гена.

• А мне - Осипа, - не уступил ему в великодушии Лима.

• Хочу быть Земляникой или Городничим, - сказал Вова.

-Нет, Городничим буду я, - хором закричали Алик и Боря. - Или Хлестаковым,

- добавили они одновременно.

Удастся ли распределить роли так, чтобы исполнители были довольны?

Решение:

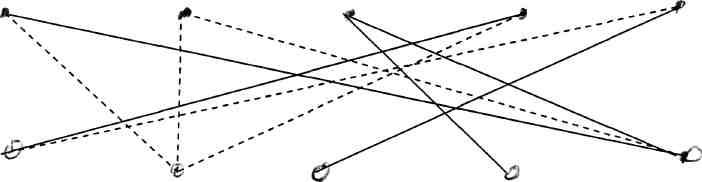
Построим граф для ситуации, описанной в задаче.

Граф

А Б В Г Л

А X О З Г

Граф с 10 вершинами и 10 ребрами. Надо выбрать из 10 пять ребер, не имеющих общих вершин: Дима - Осип, Вова - Земляника, Гена - Ляпкин-Тяпкин. Остается два случая: Алик - Хлестаков, Боря - Городничий или Алик -Городничий, Боря - Хлестаков. Как показывает граф, других решений нет.

Задача

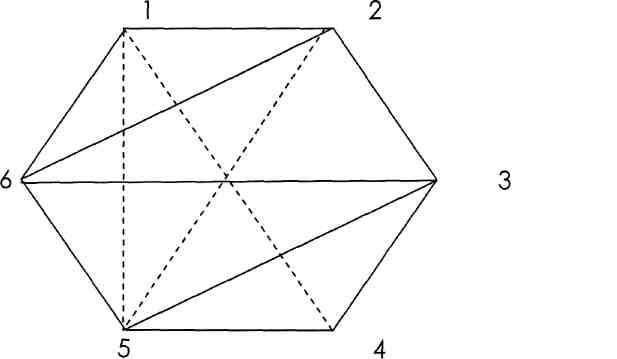
Докажите, что среди любых шести человек найдутся либо трое, друг с другом знакомые, либо трое, друг с другом незнакомые.

Решение:

Задача

В походе, который длится 12 дней, участвовали 9 человек. Каждый день дежурили 3 человека. При этом дежурные ссорились каждый день друг с другом, и никакие двое из них не хотели больше ни разу дежурить вместе. Тем не менее участники похода утверждают, что все 12 дней им удавалось назначить тройки дежурных с учетом этого требования. Могло ли так быть?

Решение:

Участники похода обозначены цифрами от 1 до 9, каждый столбец соответствует тройке дежурных.

Расписание дежурств

1	4	7	1	2	3	1	2	3	1	2	3
2	5	8	4	5	6	5	6	4	6	4	5
3	6	9	7	8	9	9	7	8	8	9	7

Можно изобразить тройки дежурных графом: участники похода обозначены точками, каждое дежурство обозначено линией одного стиля

Граф