Обыкновенные дроби

МОУ "Тырновская СОШ им. Л.А. Загоскина"    

Обыкновенные дроби

Учитель математики Пережогина Т.М.

Содержание

• Деление с остатком.
• Определение обыкновенной дроби.
• Сравнение дробей.
• Отыскание части от целого.
• Отыскание целого по его части.
• Основное свойство дроби.
• Правильные и неправильные дроби. Смешанные числа.
• Сложение и вычитание обыкновенных дробей.
• Сложение и вычитание смешанных чисел.

Деление с остатком.

382 - делимое

_382 7

35

54

7 - делитель

32

28

4

54 - неполное частное

4 - остаток

382 = 7 х 54 + 4

Задача.

Ленту длиной 1м разрезали на 3 равные части. Какова длина одной части (в метрах)?

1м

?м

1

м

1м : 3 =

Решение:

3

1

Ответ: длина одной части -

м.

3

Определение

обыкновенной дроби.

Частное от деления натуральных чисел можно записать в виде дроби.

2 : 3 = 5 : 7 =

Числитель дроби – это делимое, знаменатель – делитель, а черта дроби означает действие деление.

5

2

3

7

Сравнение дробей (с одинаковыми знаменателями) .

›

4

5

6

6

При сравнении дробей с одинаковыми

знаменателями, больше та дробь, числитель которой больше.

Сравнение дробей (с одинаковыми числителями) .

‹

3

3

4

6

При сравнении дробей с одинаковыми

числителями, больше та дробь, знаменатель которой меньше.

Отыскание части от целого.

Площадь поля – 50 га.

За день бригада трактористов

вспахала поля. Сколько га

вспахала бригада за день?

2

5

Решение:

50 : 5 х 2 = 20 (га)

Ответ: за день бригада вспахала 20 га.

Отыскание части от целого.

Чтобы найти часть от целого, надо число,

соответствующее целому, разделить на

знаменатель и результат умножить на

числитель дроби, которая выражает эту

часть.

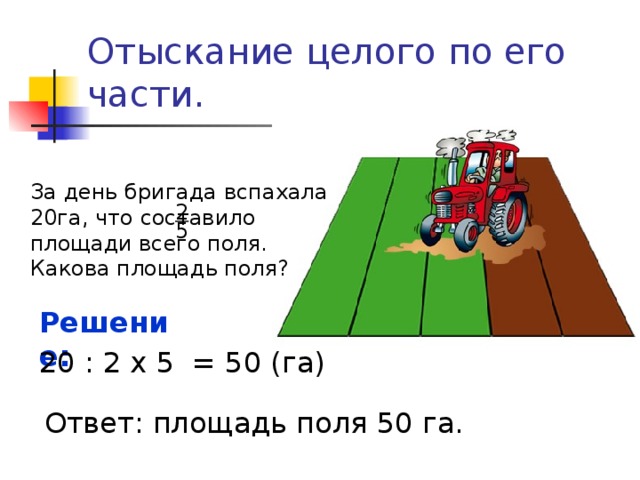
Отыскание целого по его части.

За день бригада вспахала 20га, что составило площади всего поля. Какова площадь поля?

2

5

Решение:

20 : 2 х 5 = 50 (га)

Ответ: площадь поля 50 га.

Отыскание целого по его части.

Чтобы найти целое по его части, надо число, соответствующее этой части, разделить на числитель и результат умножить на знаменатель дроби, которая выражает эту часть.

Основное свойство дроби.

2

4

Дробь можно получить из дроби умножением её числителя и знаменателя на 2:

= =

Дробь можно получить из дроби делением её числителя и знаменателя на 8:

= =

6

3

4

2

2 х 2

3 х 2

6

3

3

24

32

4

3

24 : 8

24

4

32 : 8

32

Основное свойство дроби.

При умножении или делении числителя и знаменателя дроби на одно и то же число (кроме нуля) её величина не изменяется.

a

a

a x n

a : m

=

=

b x n

b

b : m

b

Основное свойство дроби.

Представьте данную дробь в виде дроби со знаменателем 3:

12

: 6

2

=

3

: 6

18

8

: 8

1

=

3

24

: 8

2

30

: 15

=

3

45

: 15

Такое действие называют сокращением дроби.

Основное свойство дроби.

Представьте данную дробь в виде дроби со знаменателем 12:

х 4

1

4

=

3

х 4

12

х 3

3

9

=

х 3

4

12

1

х 2

2

=

6

х 2

12

Такое действие называют приведением дробей к

общему знаменателю.

Правильные и неправильные дроби. Смешанные числа.

3

7

3

1

4

5

4

Правильная дробь – это дробь, числитель которой меньше знаменателя. Такая дробь всегда меньше 1.

Смешанное число – число, содержащее в себе целую часть и правильную дробь.

Неправильная дробь – дробь, числитель которой больше или равен знаменателю. Неправильная дробь больше или равна 1.

Сложение и вычитание обыкновенных дробей.

На выпускной вечер одиннадцатых классов было куплено

6 тортов, которые были разрезаны на разное количество

одинаковых кусков. После праздника на каждом подносе

остались кусочки торта. Сколько торта осталось?

2

5

2

3

1

5

6

8

4

8

4

12

Сложение и вычитание обыкновенных дробей.

При сложении (вычитании) с одинаковыми знаменателями числители слагаемых складываются (от числителя уменьшаемого вычитается числитель вычитаемого) и результат записывается в числитель, а знаменатель остается тот же.

Сложение и вычитание смешанных чисел.

1

1

1

1

1

1

( 1 + 2 ) + ( + ) =

= =

4

2

=

+

1

4

4

4

4

1

2

1

3

3

2

4

2

4

2

2

3

1

1

3

1

2

1

2

1

1

( 2 - 1 ) + ( - ) =

2

-

=

1

3

3

3

3

3

Сложение и вычитание смешанных чисел.

Алгоритм сложения (вычитания) смешанных чисел:

1. Сложить (вычесть) целые части дробей – это целая часть суммы (разности);

2. Сложить (вычесть) дробные части – это дробная часть суммы (разности);

3. Представить результат в виде несократимого смешанного числа.