ОГЭ 2024 Декабрь Математика Вариант 1

1.  Тип 1 № 441409

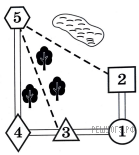Юля летом отдыхает у дедушки и бабушки в деревне Царево. Юля с дедушкой собираются съездить на машине на железнодорожную станцию Таировку. Из Царево в Таировку можно проехать по шоссе до деревни Ключи, где нужно свернуть под прямым углом налево на другое шоссе, ведущее в Таировку через поселок Демидово. Из Царево в Таировку можно проехать через поселок Демидово и не заезжая в Ключи, но тогда первую часть пути надо будет ехать по прямой лесной дороге. Есть и третий маршрут: доехать по прямой грунтовой дороге мимо озера до села Федяево и там, повернув направо, по шоссе добраться до Таировки.

По шоссе Юля с дедушкой едут со скоростью 60 км/ч, а по лесной и грунтовой дорогам  — 45 км/ч. Расстояние по шоссе от Царево до Ключей равно 72 км, от Таировки до Ключей  — 60 км, от Таировки до Демидово  — 30 км, а от Таировки до Федяево  — 27 км.

Пользуясь описанием, определите, какими цифрами на плане обозначены населенные пункты. В ответ запишите полученную последовательность пяти цифр.

2.  Тип 2 № 441410

Найдите расстояние от деревни Царево до поселка Демидово по лесной дороге. Ответ дайте в километрах.

3.  Тип 3 № 441411

Сколько минут затратят на дорогу Юля с дедушкой, если поедут на станцию через Ключи?

4.  Тип 4 № 441412

Определите, на какой маршрут до станции потребуется меньше всего времени. В ответе укажите, сколько минут потратят на дорогу Юля с дедушкой, если поедут этим маршрутом.

5.  Тип 5 № 441414

На шоссе машина дедушки расходует 6,5 литра бензина на 100 км. Известно, что на путь из Царево до Таировки через Ключи и на путь через Федяево ей необходим один и тот же объем бензина. Сколько литров бензина на 100 км машина дедушки расходует на грунтовых дорогах?

6.  Тип 6 № 110

Найдите значение выражения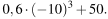  

7.  Тип 7 № 205773

На координатной прямой изображены числа a и c. Какое из следующих неравенств неверно?

1)  

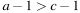
2)  

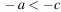
3)  

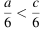
4)  

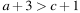
8.  Тип 8 № 311758

Найдите значение выражения 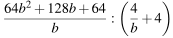при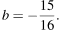

9.  Тип 9 № 137383

Решите уравнение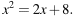

Если корней несколько, запишите их в ответ без пробелов в порядке возрастания.

10.  Тип 10 № 325540

Стрелок 4 раза стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,5. Найдите вероятность того, что стрелок первые 3 раза попал в мишени, а последний раз промахнулся.

11.  Тип 11 № 193102

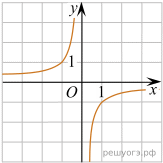
Найдите значение k по графику функции 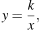изображенному на рисунке.

12.  Тип 12 № 311348

Площадь ромба 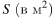   можно вычислить по формул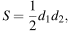е  где 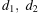   — диагонали ромба (в метрах). Пользуясь этой формулой, найдите диагональ  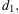если диагональ  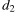  равна 30 м, а площадь ромба 120 м².

13.  Тип 13 № 320664

Укажите неравенство, которое не имеет решений.

В ответе укажите номер правильного варианта.

1)  x²​ − 64 ≤ 0

2)  x²​ + 64 ≥ 0

3)  x²​​ − 64 ≥ 0

4)  x²​​ + 64 ≤ 0

14.  Тип 14 № 394131

Вика решила начать делать зарядку каждое утро. В первый день она сделала 30 приседаний, а в каждый следующий день она делала на одно и то же количество приседаний больше, чем в предыдущий день. За 15 дней она сделала всего 975 приседаний. Сколько приседаний сделала Вика в пятый день?

15.  Тип 15 № 339389

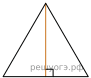Высота равностороннего треугольника равна 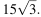Найдите его периметр.

16.  Тип 16 № 316346

Боковая сторона равнобедренного треугольника равна 4. Угол при вершине, противолежащий основанию, равен 120°. Найдите диаметр окружности, описанной около этого треугольника.

17.  Тип 17 № 314870

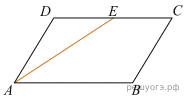Площадь параллелограмма ABCD равна 56. Точка E  — середина стороны CD. Найдите площадь трапеции AECB.

18.  Тип 18 № 438298

На клетчатой бумаге с размером клетки 1×1 изображен ромб. Найдите площадь этого ромба.

19.  Тип 19 № 169917

Какие из следующих утверждений верны?

1)  Если при пересечении двух прямых третьей прямой внутренние накрест лежащие углы составляют в сумме 90°, то эти две прямые параллельны.

2)  Если угол равен 60°, то смежный с ним равен 120°.

3)  Если при пересечении двух прямых третьей прямой внутренние односторонние углы равны 70° и 110°, то эти две прямые параллельны.

4)  Через любые три точки проходит не более одной прямой.

Если утверждений несколько, запишите их номера в порядке возрастания.

20.  Тип 20 № 311236

Разложите на множители: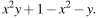

21.  Тип 21 № 348438

Имеются два сосуда, содержащие 10 кг и 16 кг раствора кислоты различной концентрации. Если их слить вместе, то получится раствор, содержащий 55% кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 61% кислоты. Сколько килограммов кислоты содержится в первом растворе?

22.  Тип 22 № 338314

Постройте график функции 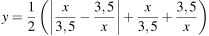и определите, при каких значениях m прямая 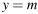имеет с графиком ровно одну общую точку.

23.  Тип 23 № 339709

Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке K. Найдите площадь параллелограмма, если BC  =  19, а расстояние от точки K до стороны AB равно 7.

24.  Тип 24 № 103

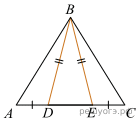На стороне АС треугольника АВС выбраны точки D и E так, что отрезки AD и CE равны (см. рис.). Оказалось, что отрезки BD и BE тоже равны. Докажите, что треугольник АВС  — равнобедренный.

25.  Тип 25 № 339373

Вершины ромба расположены на сторонах параллелограмма, а стороны ромба параллельны диагоналям параллелограмма. Найдите отношение площадей ромба и параллелограмма, если отношение диагоналей параллелограмма равно 28.