1. Тип 1 № 408268 
Общепринятые форматы листов бумаги обозначают буквой А и цифрой: А0, А1, А2 и так далее. Лист формата А0 имеет форму прямоугольника, площадь которого равна 1 кв. м. Если лист формата А0 разрезать пополам параллельно меньшей стороне, получается два равных листа формата А1. Если лист А1 разрезать так же пополам, получается два листа формата А2.
И так далее.

Отношение большей стороны к меньшей стороне листа каждого формата одно и то же, поэтому листы всех форматов подобны. Это сделано специально для того, чтобы пропорции текста и его расположение на листе сохранялись при уменьшении или увеличении шрифта при изменении формата листа.
В таблице даны размеры (с точностью до мм) четырех листов, имеющих форматы А0, А1, А3 и А4.
| Номер листа | Длина (мм) | Ширина (мм) |
| 1 | 297 | 210 |
| 2 | 420 | 297 |
| 3 | 1189 | 841 |
| 4 | 841 | 594 |
Установите соответствие между форматами и номерами листов. В ответ запишите последовательность четырех цифр, соответствующих номерам листов, без пробелов, запятых и дополнительных символов.
2. Тип 2 № 408289 
Сколько листов формата А6 получится из одного листа формата А3?
3. Тип 3 № 408294 
Найдите площадь листа формата А1. Ответ дайте в квадратных сантиметрах.
4. Тип 4 № 408314 
Найдите отношение длины меньшей стороны листа формата А3 к большей. Ответ округлите до десятых.
5. Тип 5 № 408323 
Бумагу формата А5 упаковали в пачки по 500 листов. Найдите массу пачки, если масса бумаги площади 1 кв. м равна 80 г. Ответ дайте в граммах.
6. Тип 6 № 349924 
Найдите значение выражения 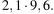
7. Тип 7 № 317102 
На координатной прямой точками A, B, C и D отмечены числа 0,098; −0,02; 0,09; 0,11. Какой точкой изображается число 0,09?

В ответе укажите номер правильного варианта.
1) A
2) B
3) C
4) D
8. Тип 8 № 311471 
Упростите выражение 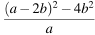 и найдите его значение при
и найдите его значение при 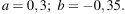
9. Тип 9 № 353555 
Решите уравнение 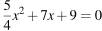
Если корней несколько, запишите их в ответ без пробелов в порядке возрастания.
10. Тип 10 № 132728 
Коля выбирает трехзначное число. Найдите вероятность того, что оно делится на 5.
11. Тип 11 № 333008 
На рисунке изображен график функции y = ax2 + bx + c . Установите соответствие между утверждениями и промежутками, на которых эти утверждения выполняются. Впишите в приведенную в ответе таблицу под каждой буквой соответствующую цифру.
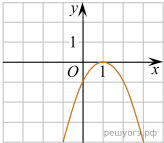
| УТВЕРЖДЕНИЯ | | ПРОМЕЖУТКИ |
| А) функция возрастает на промежутке Б) функция убывает на промежутке | | 1) [1; 2] 2) [0; 2] 3) [−1; 0] 4) [−2; 3] |
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
12. Тип 12 № 46 
Период колебания математического маятника T (в секундах) приближенно можно вычислить по формуле 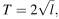 где l — длина нити (в метрах). Пользуясь этой формулой, найдите длину нити маятника (в метрах), период колебаний которого составляет 3 секунды.
где l — длина нити (в метрах). Пользуясь этой формулой, найдите длину нити маятника (в метрах), период колебаний которого составляет 3 секунды.
13. Тип 13 № 185 
Решение какого из данных неравенств изображено на рисунке?
В ответе укажите номер правильного варианта.

1) 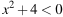
2) 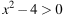
3) 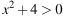
4) 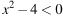
14. Тип 14 № 394460 
Два приятеля положили в банк по 10000 рублей каждый, причем первый положил деньги на вклад с ежеквартальным начислением 10%, а второй — с ежегодным начислением 45%. Через год приятели получили деньги вместе с причитающимися им процентами. Кто получил большую прибыль? В ответе напишите 1, если большую прибыль получит первый приятель, или 2, если второй.
15. Тип 15 № 311759 
Четырехугольник ABCD вписан в окружность. Угол ABC равен 136°, угол CAD равен 82°. Найдите угол ABD. Ответ дайте в градусах.
16. Тип 16 № 356399 
 Сторона квадрата равна 6. Найдите радиус окружности, вписанной в этот квадрат.
Сторона квадрата равна 6. Найдите радиус окружности, вписанной в этот квадрат.
17. Тип 17 № 438297 
 Диагонали AC и BD параллелограмма ABCD пересекаются в точке O, AC = 26, BD = 30, AB = 7. Найдите DO.
Диагонали AC и BD параллелограмма ABCD пересекаются в точке O, AC = 26, BD = 30, AB = 7. Найдите DO.
18. Тип 18 № 311485 
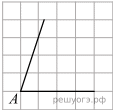 На квадратной сетке изображен угол A. Найдите
На квадратной сетке изображен угол A. Найдите 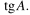
19. Тип 19 № 169915 
Какие из следующих утверждений верны?
1) Если угол равен 45°, то вертикальный с ним угол равен 45°.
2) Любые две прямые имеют ровно одну общую точку.
3) Через любые три точки проходит ровно одна прямая.
4) Если расстояние от точки до прямой меньше 1, то и длина любой наклонной, проведенной из данной точки к прямой, меньше 1.
20. Тип 20 № 311237 
Решите неравенство 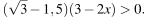
21. Тип 21 № 338919 
Первые 300 км автомобиль ехал со скоростью 60 км/ч, следующие 300 км — со скоростью 100 км/ч, а последние 300 км — со скоростью 75 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.
22. Тип 22 № 127 
При каком значении p прямая 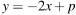 имеет с параболой
имеет с параболой 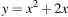 ровно одну общую точку? Найдите координаты этой точки. Постройте в одной системе координат данную параболу и прямую при найденном значении p.
ровно одну общую точку? Найдите координаты этой точки. Постройте в одной системе координат данную параболу и прямую при найденном значении p.
23. Тип 23 № 311700 
Найдите отношение двух сторон треугольника, если его медиана, выходящая из их общей вершины, образует с этими сторонами углы в 30° и 90°.
24. Тип 24 № 314822 
В параллелограмме ABCD диагонали AC и BD пересекаются в точке K. Докажите, что площадь параллелограмма ABCD в четыре раза больше площади треугольника AKD.
25. Тип 25 № 156 
Медиана BM треугольника ABC является диаметром окружности, пересекающей сторону BC в ее середине. Длина стороны AC равна 4. Найдите радиус описанной окружности треугольника ABC.










 Сторона квадрата равна 6. Найдите радиус окружности, вписанной в этот квадрат.
Сторона квадрата равна 6. Найдите радиус окружности, вписанной в этот квадрат. Диагонали AC и BD параллелограмма ABCD пересекаются в точке O, AC = 26, BD = 30, AB = 7. Найдите DO.
Диагонали AC и BD параллелограмма ABCD пересекаются в точке O, AC = 26, BD = 30, AB = 7. Найдите DO. На квадратной сетке изображен угол A. Найдите
На квадратной сетке изображен угол A. Найдите 




















