Олимпиадные задания по математике для проведения школьного этапа Всероссийской олимпиады школьников в 2015 - 2016 уч. году. ( 9 класс)

Олимпиадные задания

по математике для проведения школьного этапа Всероссийской олимпиады школьников в 2015 - 2016 уч. году.

( 9 класс)

9 класс

Задача №1 Электрический провод длиной 25м. ночью был перерезан где - то в одном месте. Можно ли из образовавшихся двух частей провода вырезать куски длиной 1,2,3,6 и 12м?

Задача №2. Можно ли представить дробь в виде суммы двух дробей, числители которых равны 1, а знаменатели - различные целые числа?

Задача №3. На основаниях АВ и СD трапеции ABCDвзяты точки K и L. Пусть Е - точка пересечения отрезков AL и DK, F- точка пересечения BL и CK. Доказать, что сумма площадей треугольников ADE и BCF равна площади четырехугольника EKFL.

Задача №4 Пусть D- дискриминант приведенного квадратного трехчлена x²+ax+b. Найдите корни трехчлена, если известно, что они различны и один из них равен D, а другой равен 2D.

Задача №5 Докажите, что если а≥1, b≤-3, то

Общие положения о проверке работ

Приведённые ниже решения задач не являются единственно возможными. Участники, вероятно, найдут и другие верные решения. При проверке и оценке решения учитывается только его верность и полнота. Приведённые ниже критерии по проверке задач также носят рекомендательный характер и могут быть уточнены и дополнены школьным жюри олимпиады в соответствии с особенностями решений школьников данной школы. Каждая задача оценивается целым числом баллов от 0 до 7. Итог подводится по сумме баллов, набранных участником.

Основные принципы оценивания задач :

7баллов - Полное верное решение.

6-7баллов Верное решение. Имеются небольшие недочеты, в целом не влияющие на решение

5-6баллов Решение в целом верное. Однако оно содержит ряд ошибок, либо не рассмотрение отдельных случаев, но может стать правильным после небольших исправлений или дополнений.

4балла Верно рассмотрен один из двух (более сложный) существенных случаев.

2-3балла Доказаны вспомогательные утверждения, помогающие в решении задачи.

1балл Рассмотрены отдельные важные случаи при отсутствии решения (или при ошибочном решении).

0баллов Решение неверное, продвижения отсутствуют.

0 баллов Решение отсутствует.

Олимпиадная работа не является контрольной работой участника, поэтому любые исправления в работе, в том числе зачеркивание ранее написанного текста, не являются основанием для снятия баллов; недопустимо снятие баллов в работе за неаккуратность записи решений при ее выполнении. Баллы не выставляются «за старание участника», в том числе за запись в работе большого по объему текста, но не содержащего продвижений в решении задачи. Победителем в параллели считается участник, набравший наибольший суммарный балл и решивший не менее половины задач (не менее трех задач). Победителей в параллели может быть несколько. Призерами рекомендуется считать участников, решивших не менее половины задач, но набравших меньше баллов, чем победитель. Если ни один участник в данной параллели не решил более двух задач, жюри может принять решение считать призерами участников, решивших две задачи, однако победителей в этом случае не будет.

Задача №1 Электрический провод длиной 25м. ночью был перерезан где - то в одном месте. Можно ли из образовавшихся двух частей провода вырезать куски длиной 1,2,3,6 и 12м?

Решение: Можно. Нужные куски можно получить, например, следующим образом:

Выбрав из образовавшихся частей ту, которая не короче другой(и следовательно не короче 12,5м), вырезаем из нее и откладываем в сторону 12 метровый кусок. У нас остается две части, сумма которых равна 13 м. По крайней мере одна из этих частей будет не короче 6,5м; вырезаем и откладываем в сторону 6 - метровый кусок и т.д. (Оставаться будут пары частей с суммами 7м, 4м, 2м и вырезаются куски, длиной 3м,2м и 1м соответственно).

Ответ: можно.

Задача №2. Можно ли представить дробь в виде суммы двух дробей, числители которых равны 1, а знаменатели - различные целые числа?

Решение: можно, например,

Ответ: можно

Задача №3. На основаниях АВ и СD трапеции ABCDвзяты точки K и L. Пусть Е - точка пересечения отрезков AL и DK, F- точка пересечения BL и CK. Доказать, что сумма площадей треугольников ADE и BCF равна площади четырехугольника EKFL.

Решение: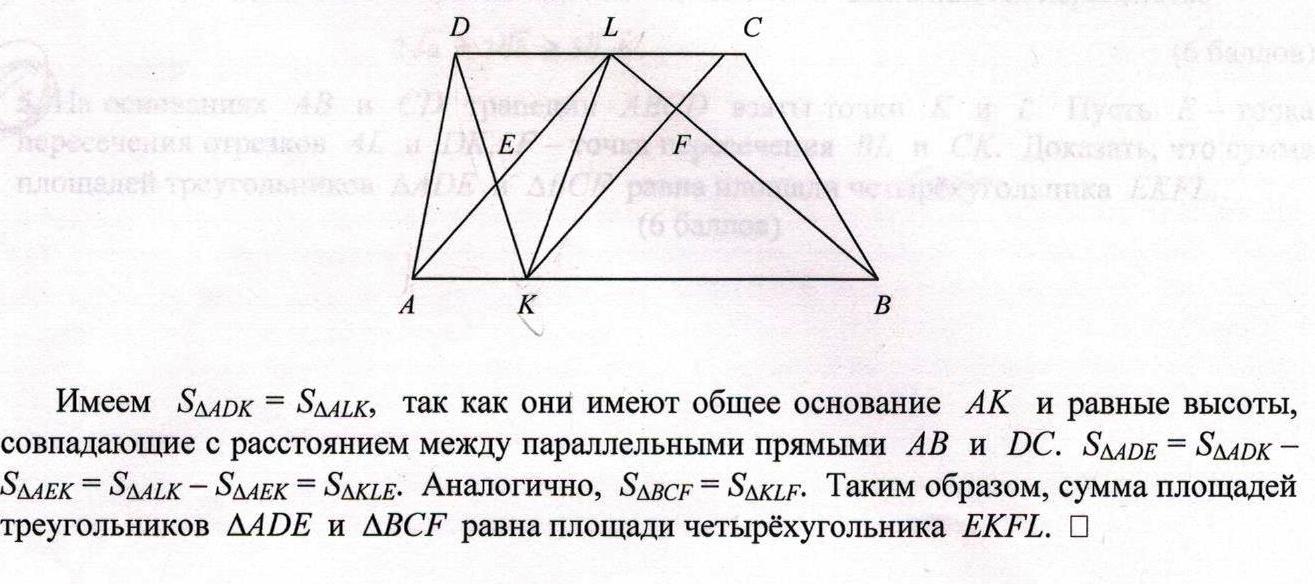

Задача №4 Пусть D- дискриминант приведенного квадратного трехчлена x²+ax+b. Найдите корни трехчлена, если известно, что они различны и один из них равен D, а другой равен 2D.

Решение: по теореме Винта b=D×2D= 2D²

a= -(D+2D)= -3D

т.е. трехчлен равен x²-3Dx+2D². Его дискриминант D= (-3D)²- 4 ×2D², откуда D=D², т.е. D=0(в этом случае оба корня одинаковые и равны 0) или D=1( в этом случае корни равны 1 и 2).

Ответ: 1и 2.

Задача №5 Докажите, что если а≥1, b≤-3, то .

Решение: Так как а≥1, b≤-3,то a-b≥-4 . Возведем последнее неравенство в квадрат (это можно сделать, так как обе части неравенства положительны)

(a-b)²≥16

Преобразовывая, получим:

a²-2ab+b²≥16,

a²-2ab+b²≥16+4ab,

(a-b)²≥16+4ab,

.