Просмотр содержимого документа
«Определители и векторы»
Çyzykly deňlemeler ulgamyny Krameriň düzgüni bilen çözmek
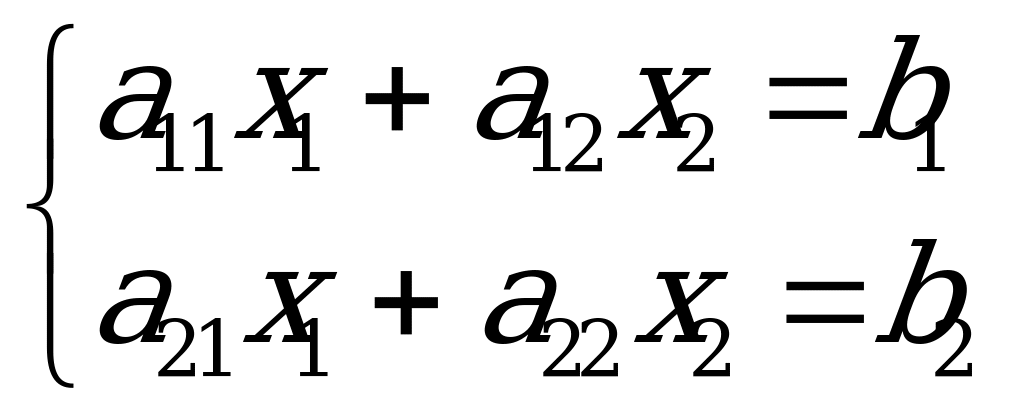 .
.
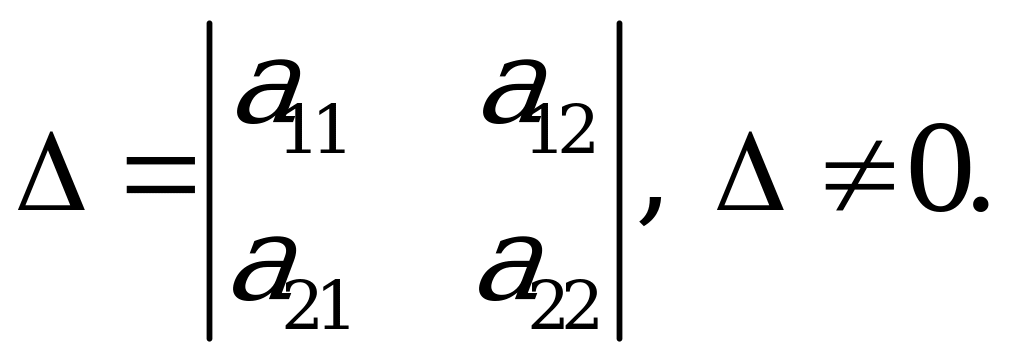
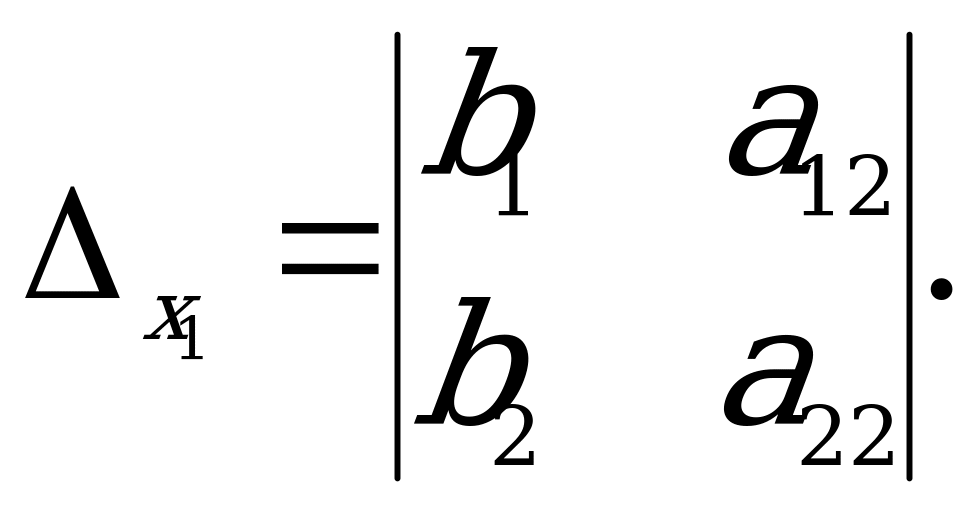
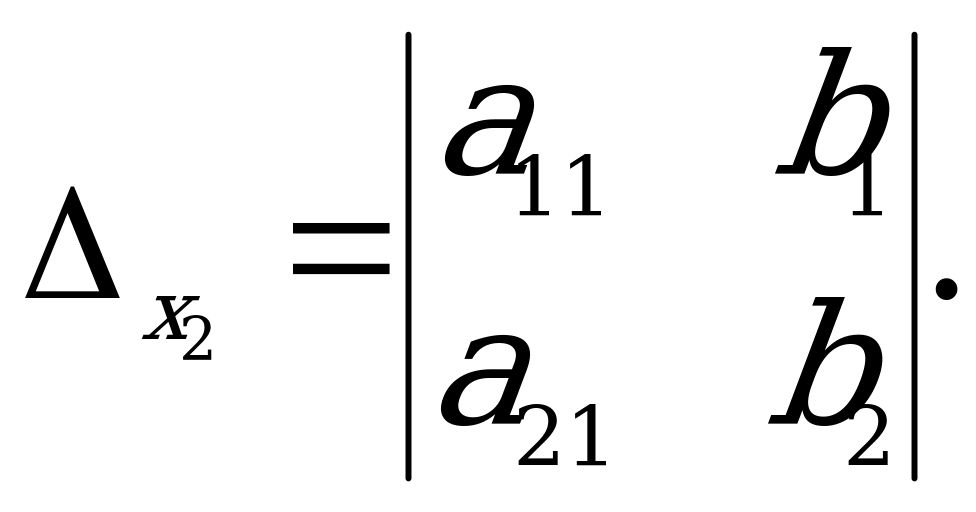 Bu ýerden
Bu ýerden 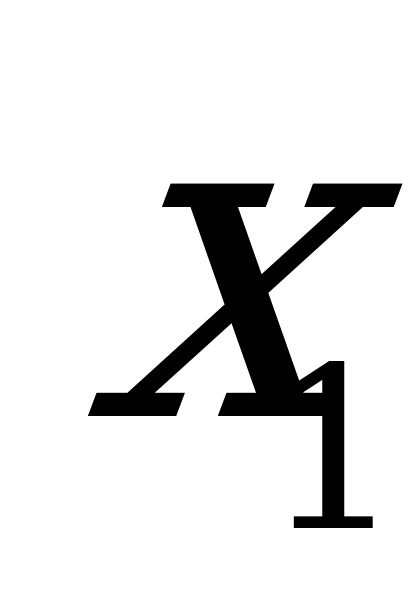 we
we 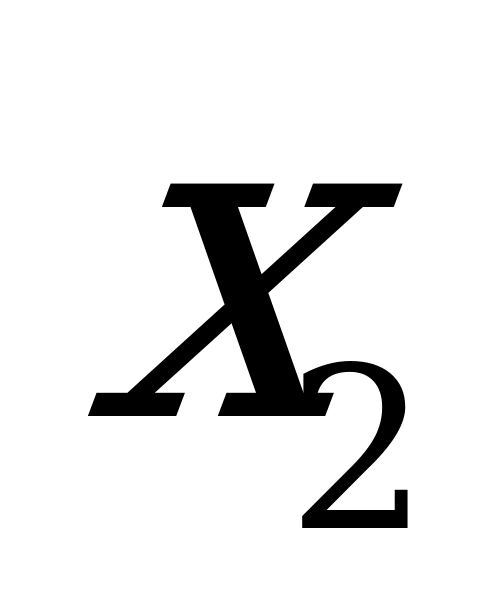 näbellileri tapmak üçin
näbellileri tapmak üçin 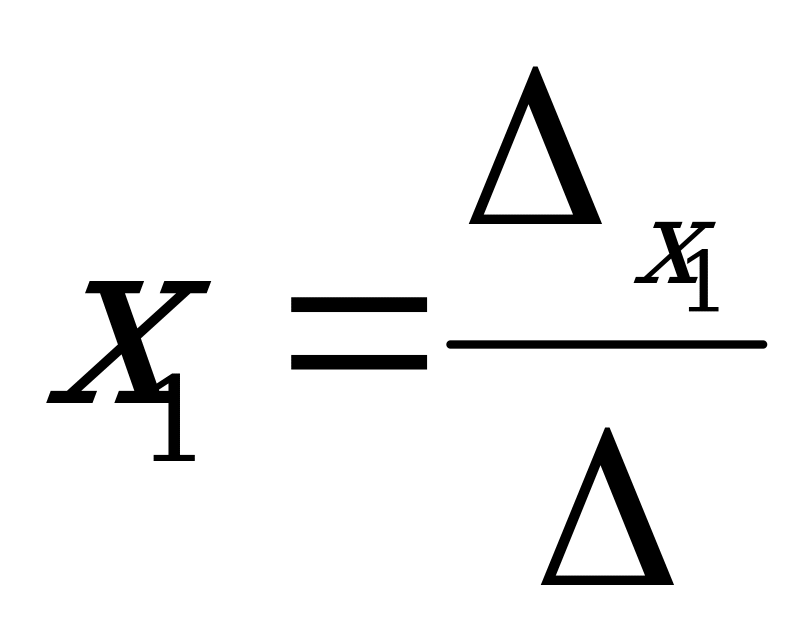 ,
, 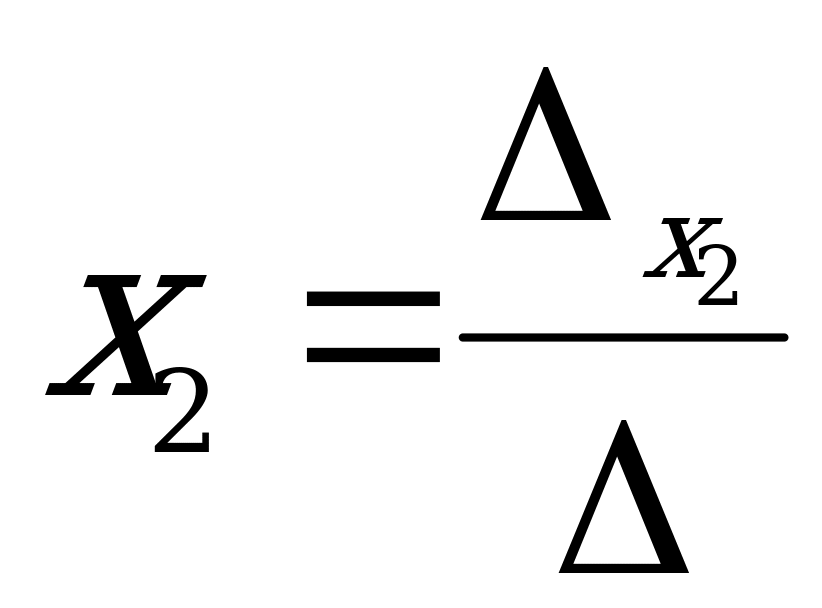 .
.
MATRISALAR
Matrisany sana köpeltmek
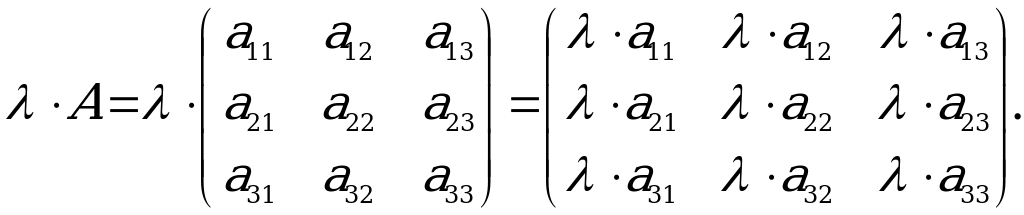
Matrisalary goşmak we aýyrmak
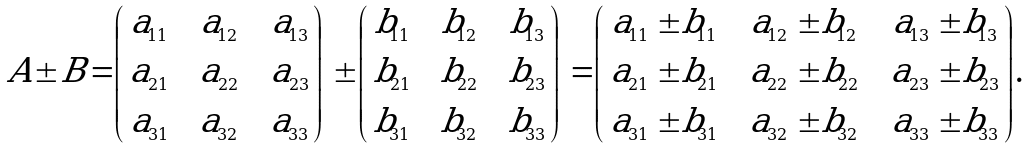
Matrisalary köpeltmek
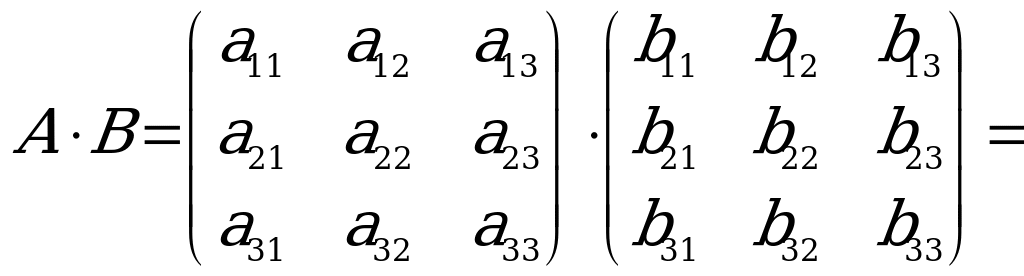


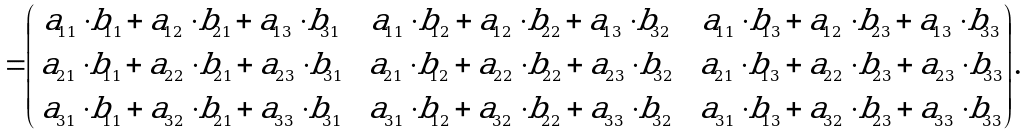
Ters matrisa
n-nji tertipli A kwadrat matrisa seredeliň. A matrisanyň ters matrisasy diýip 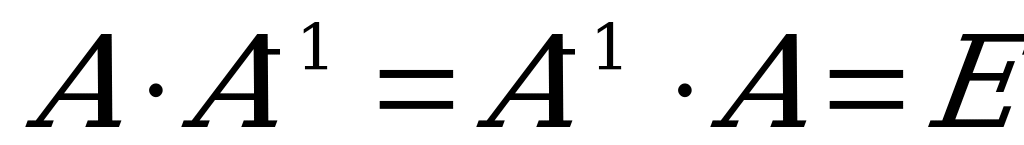 deňligi kanagatlandyrýan, n-nji tertipli
deňligi kanagatlandyrýan, n-nji tertipli 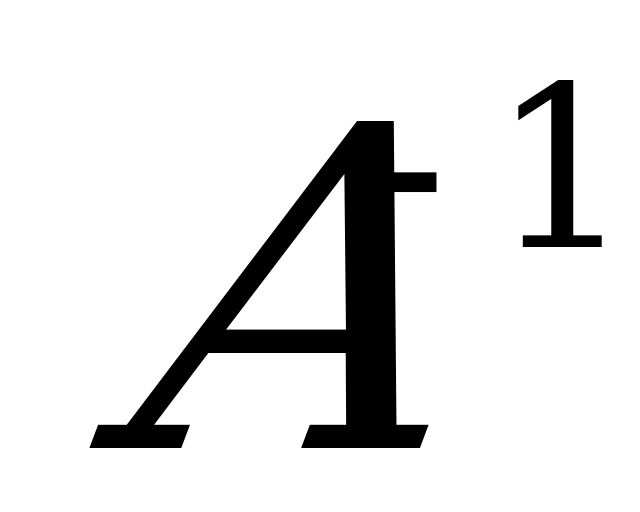 matrisa aýdylýar. Kesgitleýjisi
matrisa aýdylýar. Kesgitleýjisi 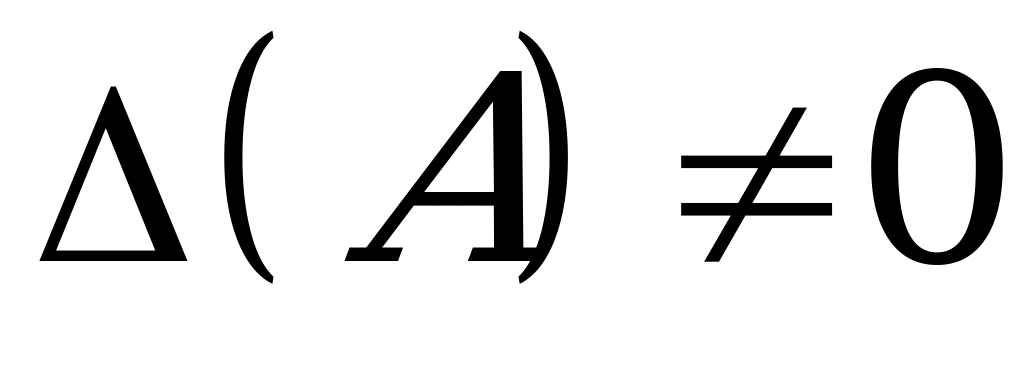 bolan islendik A matrisanyň ters matrisasy bardyr. Ters matrisany, esasan:
bolan islendik A matrisanyň ters matrisasy bardyr. Ters matrisany, esasan: 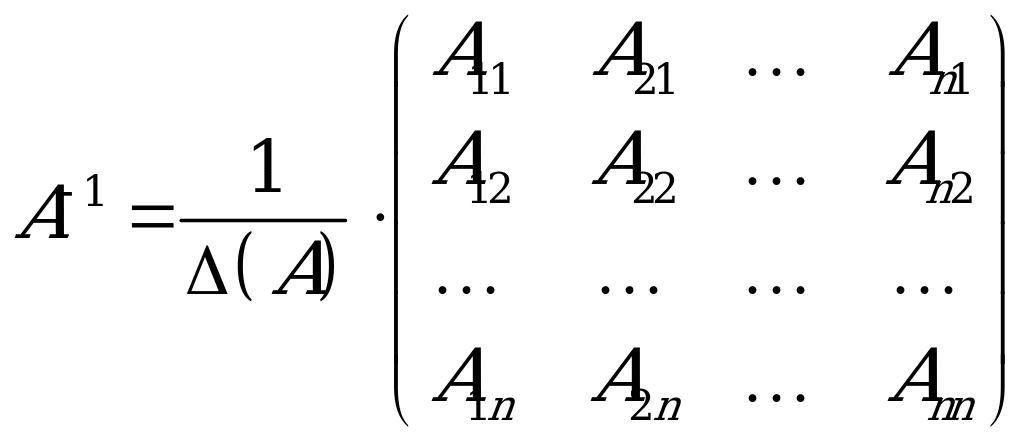
formula boýunça tapýarlar. 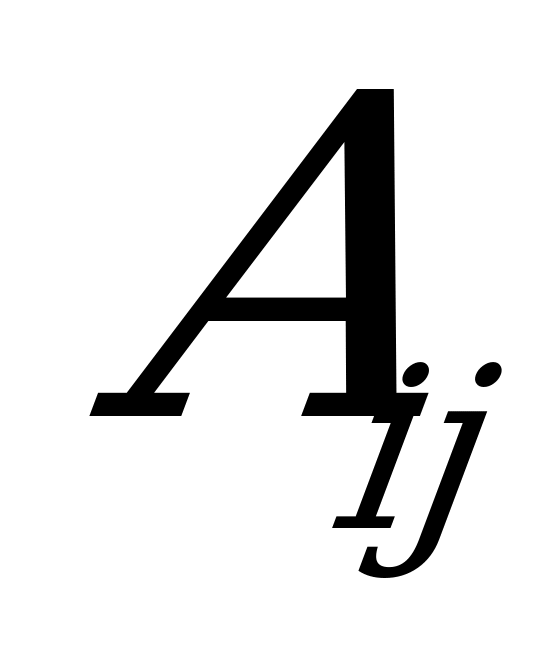 belgileme A matrisanyň
belgileme A matrisanyň  elementiniň algebraik doldurgyjydyr:
elementiniň algebraik doldurgyjydyr: 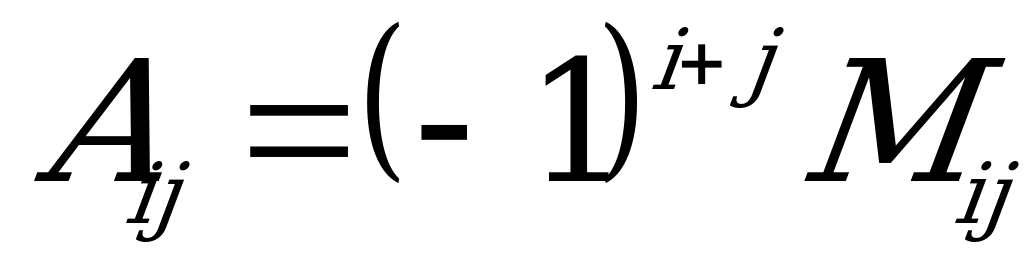 .
.
K ESGITLEÝJILERIŇ HASAPLANYŞY
ESGITLEÝJILERIŇ HASAPLANYŞY
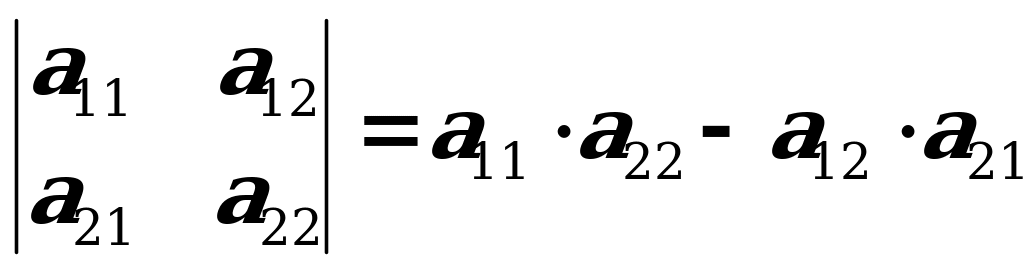 .
.
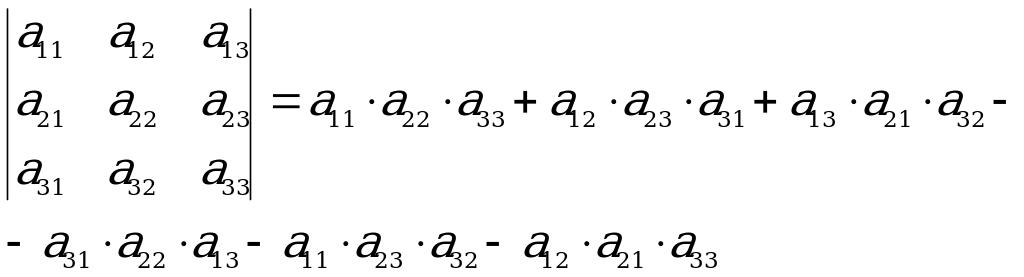
Üçünji tertipli kesgitleýjini hasaplamakda aşakdaky shemany ulanmak amatlydyr:
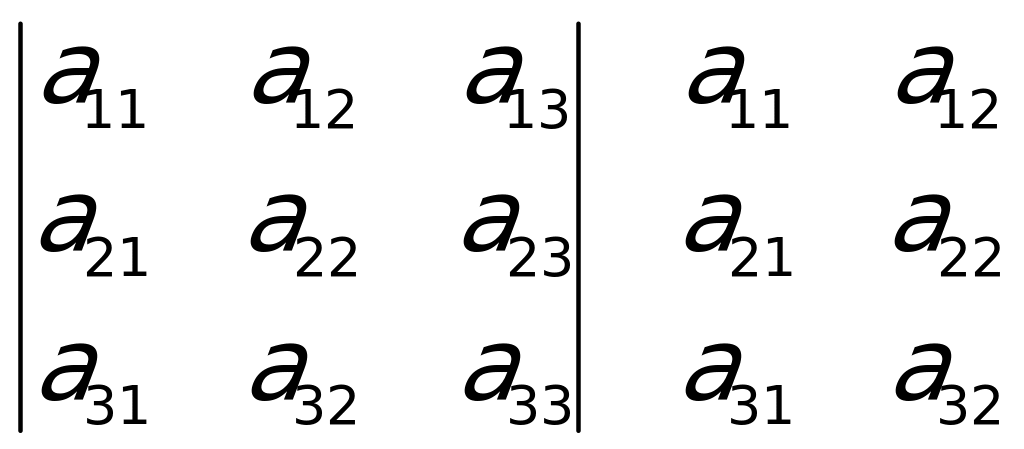
 .
.  .
.
Kesgitleýjini i-nji setiriň elementleri boýunça dargadyp, şeýle ýazmak bolar: 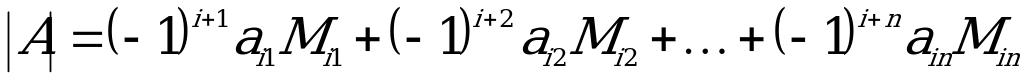 ,
,
bu ýerde  arkaly
arkaly  matrisanyň i-nji setirini we j-nji sütünini çyzmakdan galýan (n-1)-nji tertipli kesgitleýji – minor belgilenendir.
matrisanyň i-nji setirini we j-nji sütünini çyzmakdan galýan (n-1)-nji tertipli kesgitleýji – minor belgilenendir.
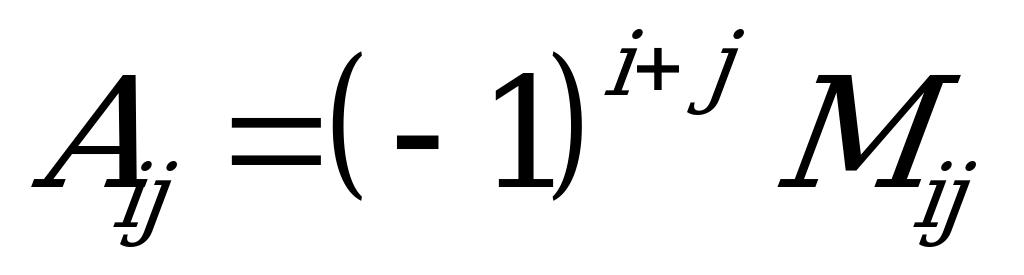 ululyga
ululyga  elementiň algebraik doldurgyjy diýilýär. Onda (*) dargatmany şeýle ýazmak bolar:
elementiň algebraik doldurgyjy diýilýär. Onda (*) dargatmany şeýle ýazmak bolar:
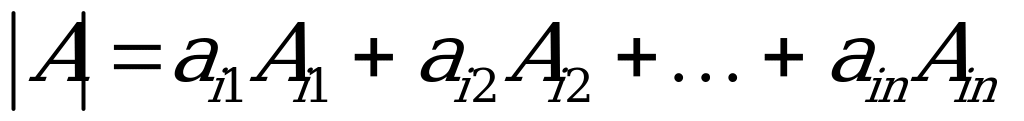 . (**)
. (**)
(**) formula boýunça 4-nji tertipli kesgitleýjini 1-nji setiriň elementleri boýunça dargadyp alarys:
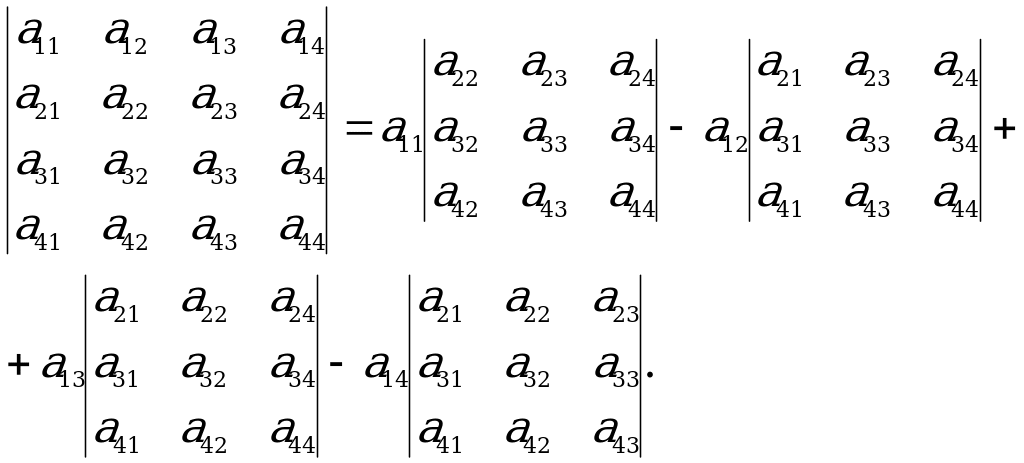
WEKTORLARYŇ SKALÝAR KÖPELTMEK HASYLY
 we
we  wektorlaryň skalýar köpeltmek hasyly şeýle bir c san bolup,
wektorlaryň skalýar köpeltmek hasyly şeýle bir c san bolup, 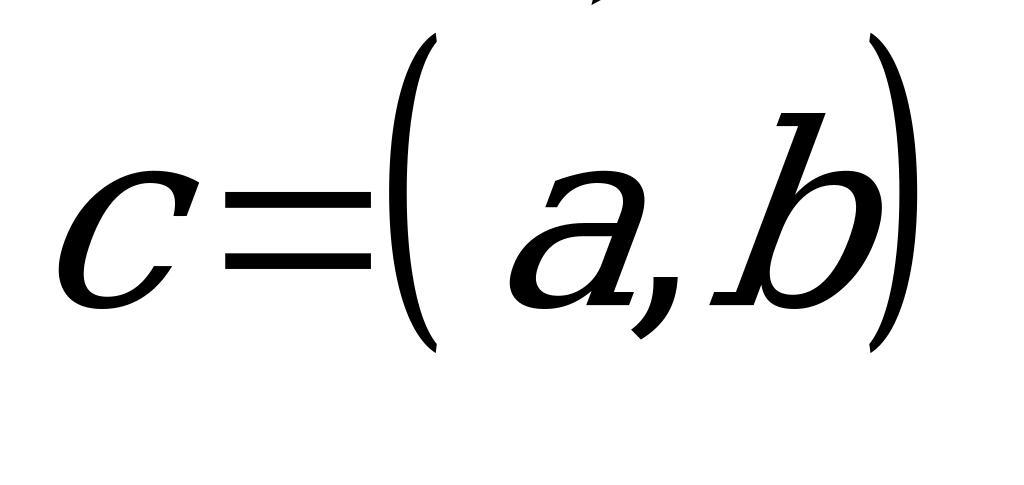 ýa-da
ýa-da 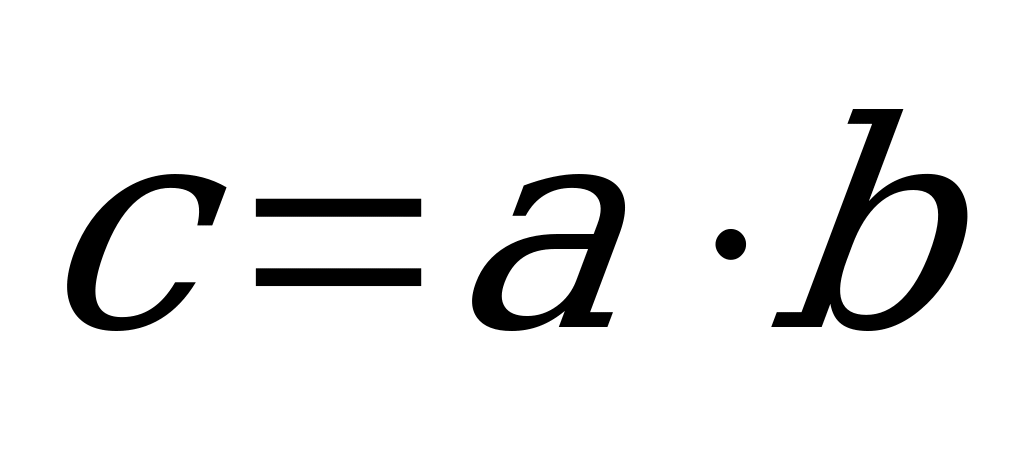 ýaly belgilenilýär we şeýle formula bilen kesgitlenýär:
ýaly belgilenilýär we şeýle formula bilen kesgitlenýär: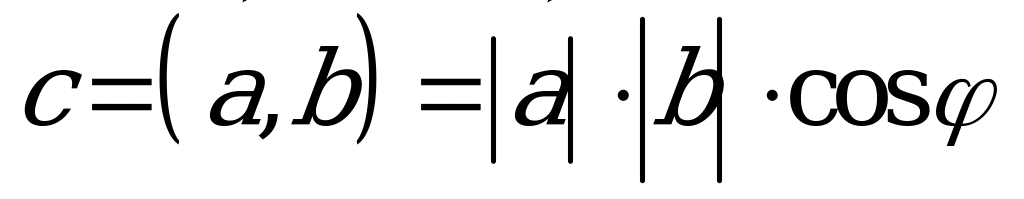 ,bu ýerde –
,bu ýerde – 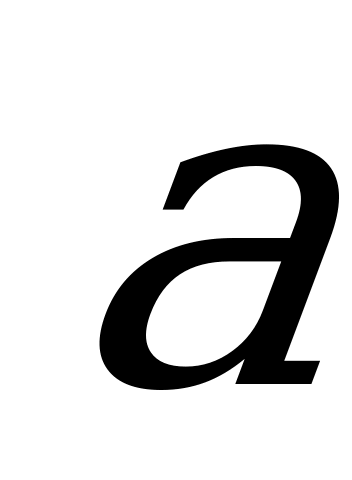 we
we  wektorlaryň arasyndaky burçdur. Wektoryň öz-özüne skalýar köpeltmek hasyly onuň modulynyň kwadratyna deňdir:
wektorlaryň arasyndaky burçdur. Wektoryň öz-özüne skalýar köpeltmek hasyly onuň modulynyň kwadratyna deňdir: 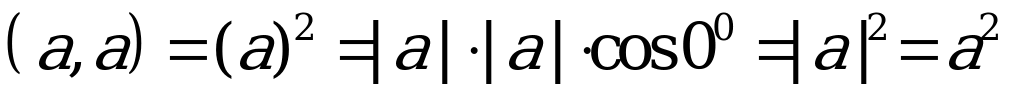 .
.
Eger wektorlar gönüburçly koordinatlar tekizliginde
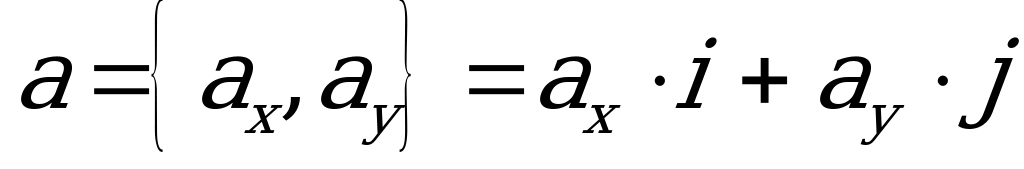 ,
, 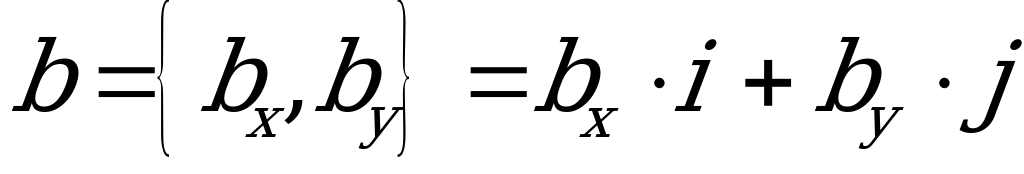
koordinatlary bilen berlen bolsalar, onda olaryň skalýar köpeltmek hasyly 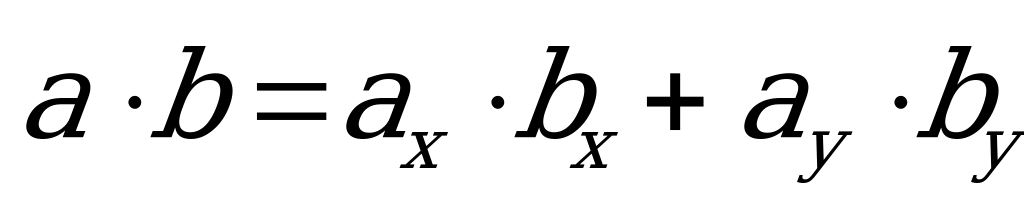 .
.
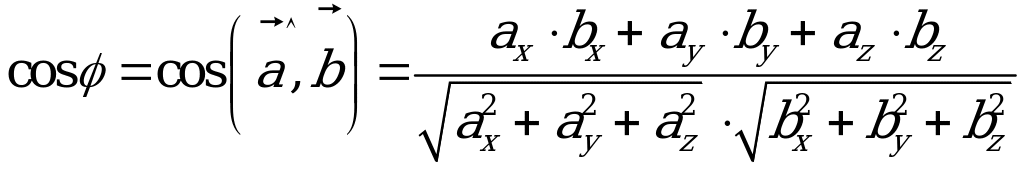 .
.
Berlen  wektor bilen
wektor bilen  ,
,  ,
, 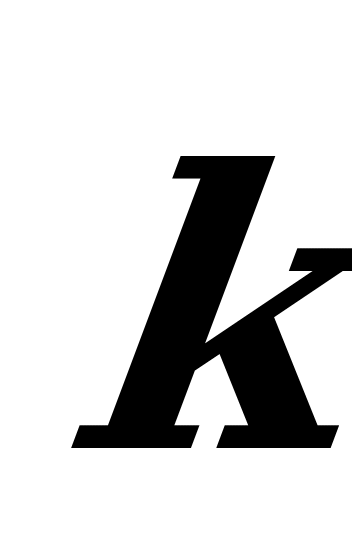 ortlar arasyndaky , , burçlarynyň kosinuslaryna ugrukdyryjy kosinuslar diýilýär we olar şeýle tapylýarlar:
ortlar arasyndaky , , burçlarynyň kosinuslaryna ugrukdyryjy kosinuslar diýilýär we olar şeýle tapylýarlar: 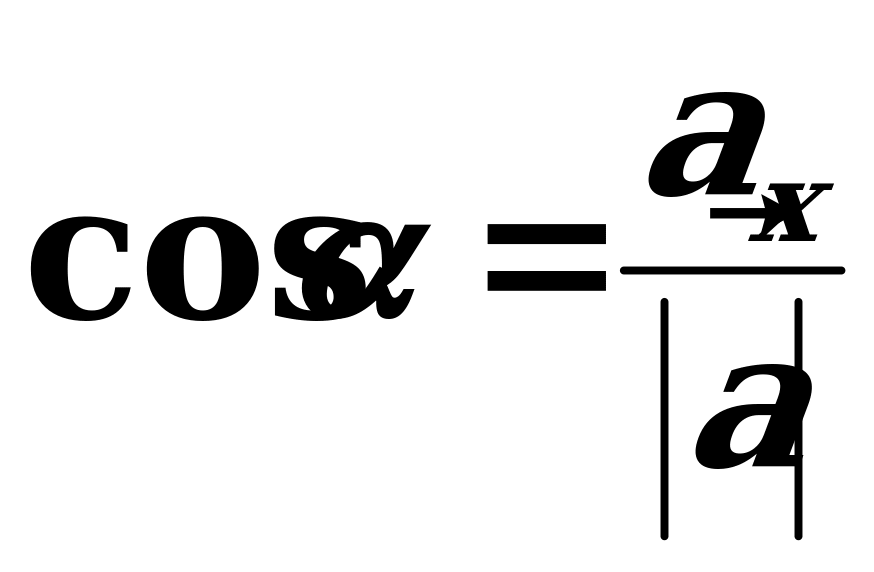 ,
, 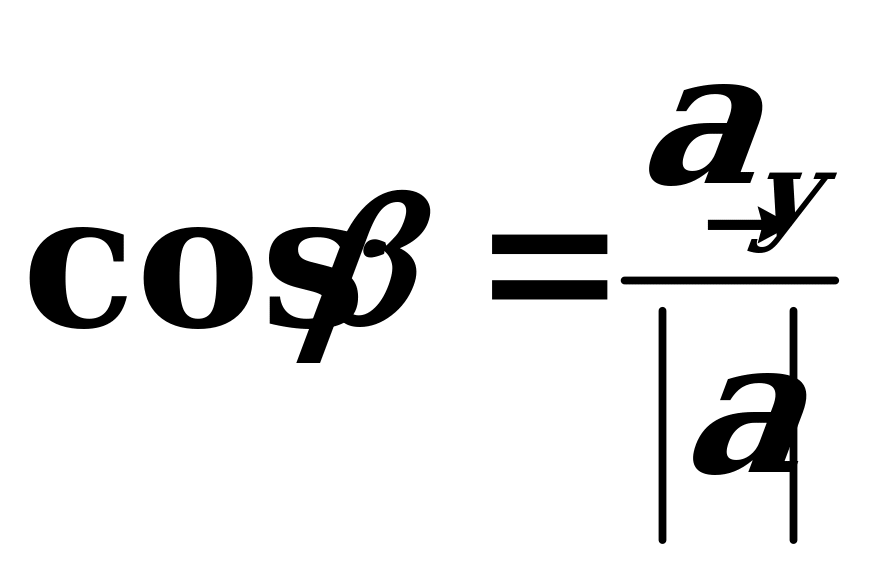 ,
,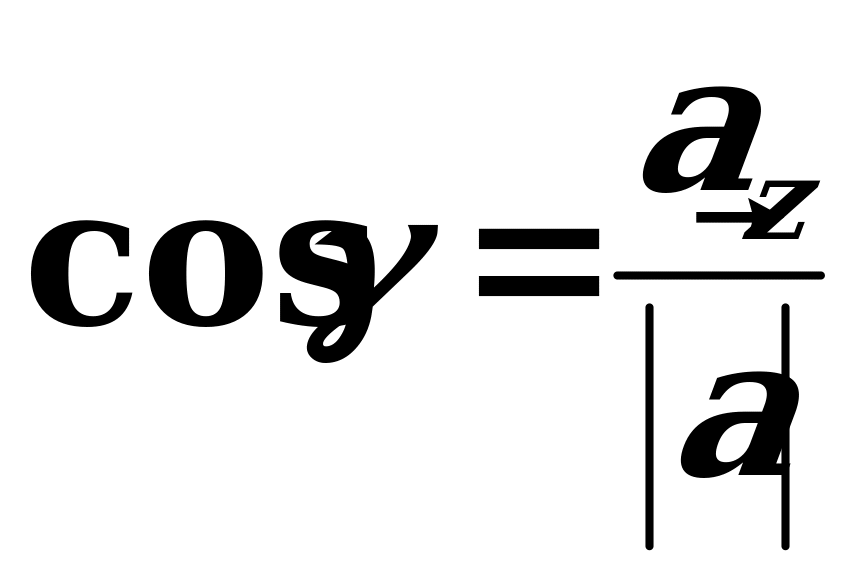 (giňişlikde).
(giňişlikde).
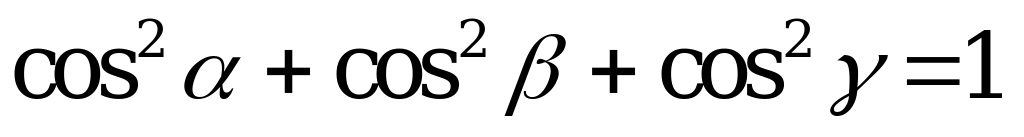 .
. 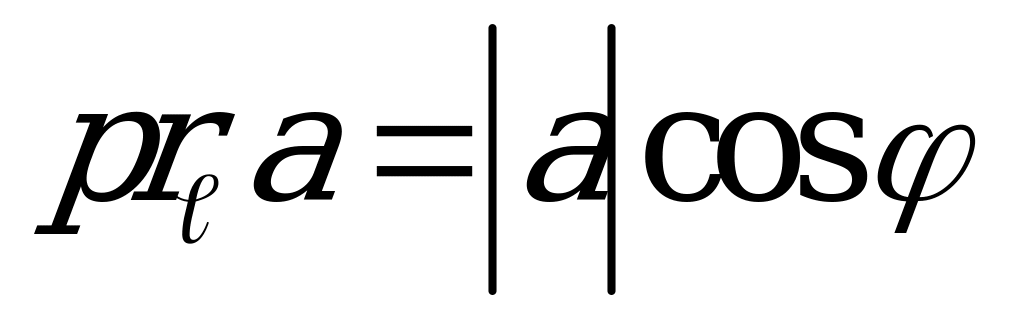 wektoryň oka bolan proýeksiýasy.
wektoryň oka bolan proýeksiýasy.
WEKTORLARYŇ WEKTOR KÖPELTMEK HASYLY
 we
we  wektorlaryň wektor köpeltmek hasyly şeýle bir
wektorlaryň wektor köpeltmek hasyly şeýle bir  wektor bolup,
wektor bolup, 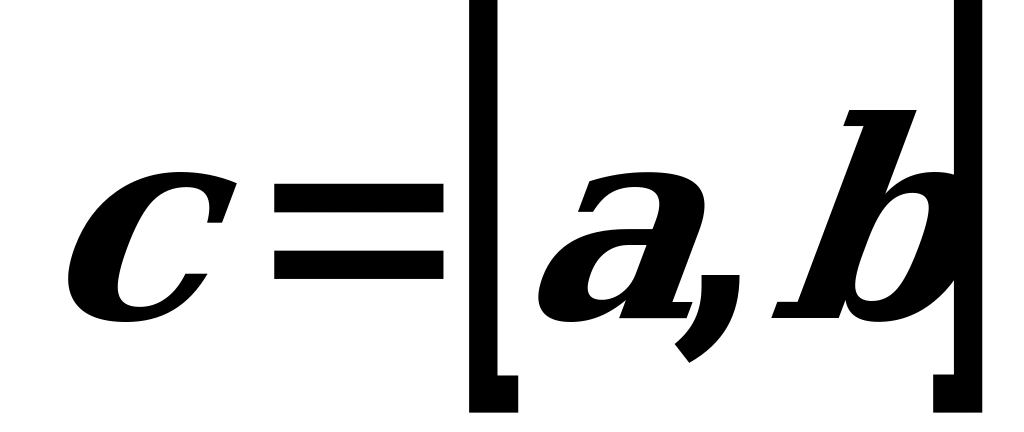 ýa-da
ýa-da 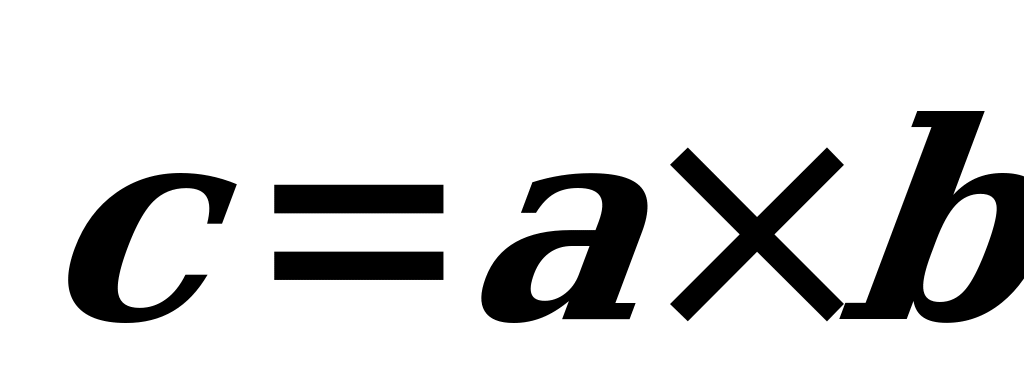 ýaly belgilenilýär we aşakdaky üç şert boýunça kesgitlenýär:
ýaly belgilenilýär we aşakdaky üç şert boýunça kesgitlenýär:
 wektoryň moduly
wektoryň moduly  we
we  wektorlaryň üstünde gurlan parallelogramyň meýdanyna deňdir:
wektorlaryň üstünde gurlan parallelogramyň meýdanyna deňdir: 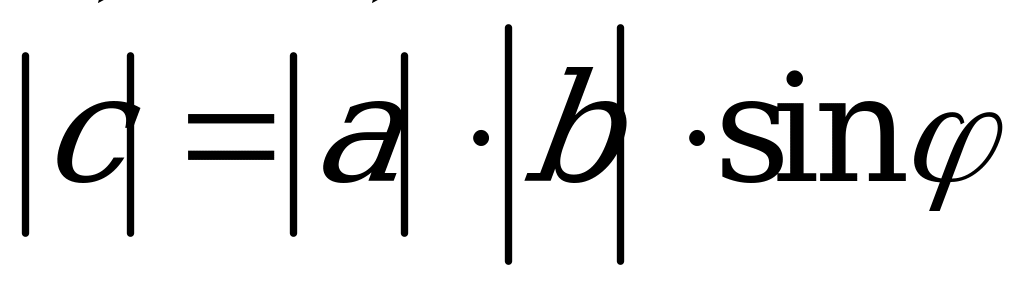 .
.
 wektor
wektor  we
we  wektorlaryň her birine, diýmek olaryň ýatan tekizligine perpendikulýardyr:
wektorlaryň her birine, diýmek olaryň ýatan tekizligine perpendikulýardyr:  we
we 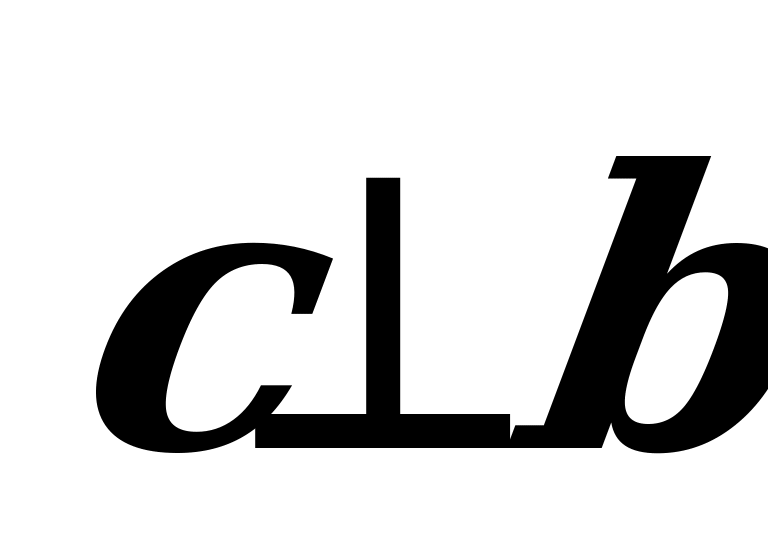 .
.
Bir başlangyçdan alnyp goýlan  ,
, 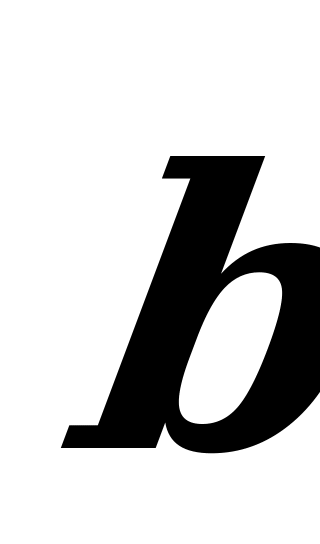 we
we 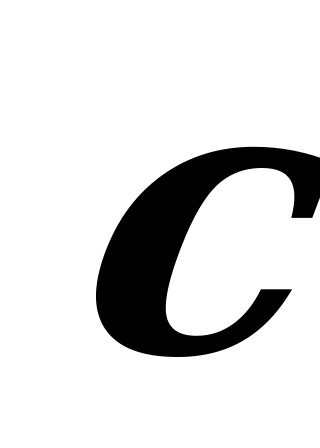 wektorlar wektorlaryň sagky üçlügini emele getirýärler.
wektorlar wektorlaryň sagky üçlügini emele getirýärler.

Wektorlar özara kollinear bolanda ýa-da birden-biri nul wektor bolsa, wektor köpeltmek hasyly nula deňdir. Wektoryň öz-özüne wektor köpeltmek hasyly nul wektora deňdir: 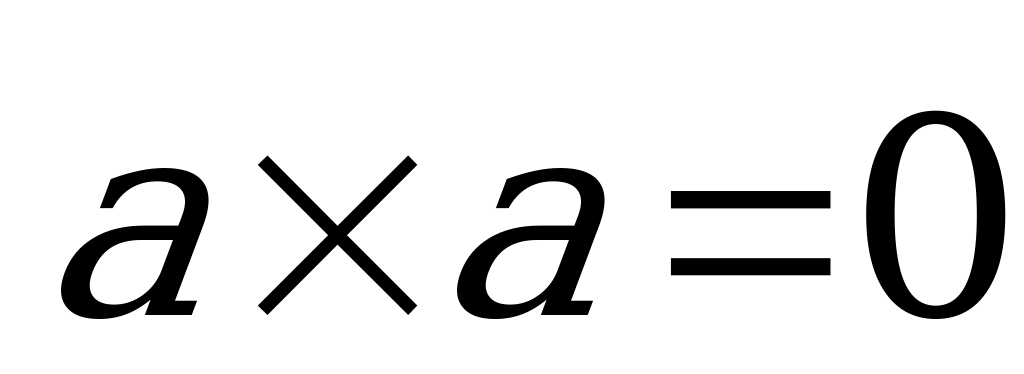 . Eger
. Eger  we
we 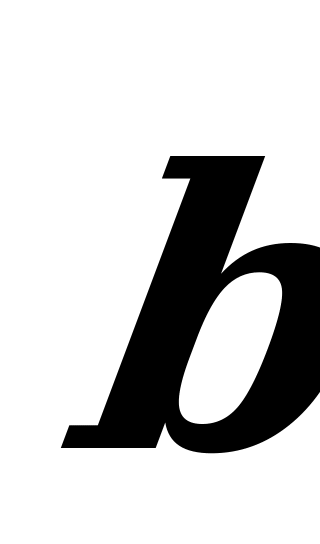 wektorlar giňişlikde, gönüburçly koordinatlar ulgamynda özleriniň koordinatlary bilen berlen bolsa, onda olaryň wektor köpeltmek hasyly şeýle hasaplanylýar:
wektorlar giňişlikde, gönüburçly koordinatlar ulgamynda özleriniň koordinatlary bilen berlen bolsa, onda olaryň wektor köpeltmek hasyly şeýle hasaplanylýar:
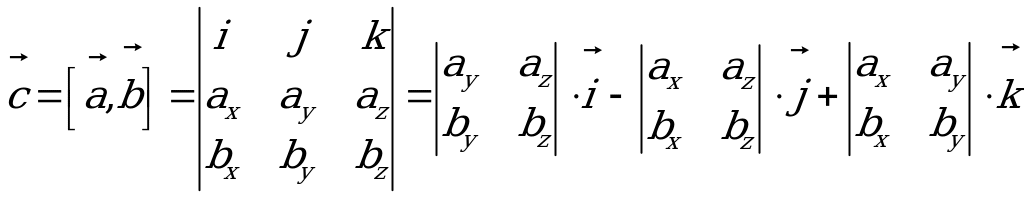
 we
we  wektorlaryň üstünde gurlan üçburçlugyň meýdany:
wektorlaryň üstünde gurlan üçburçlugyň meýdany: 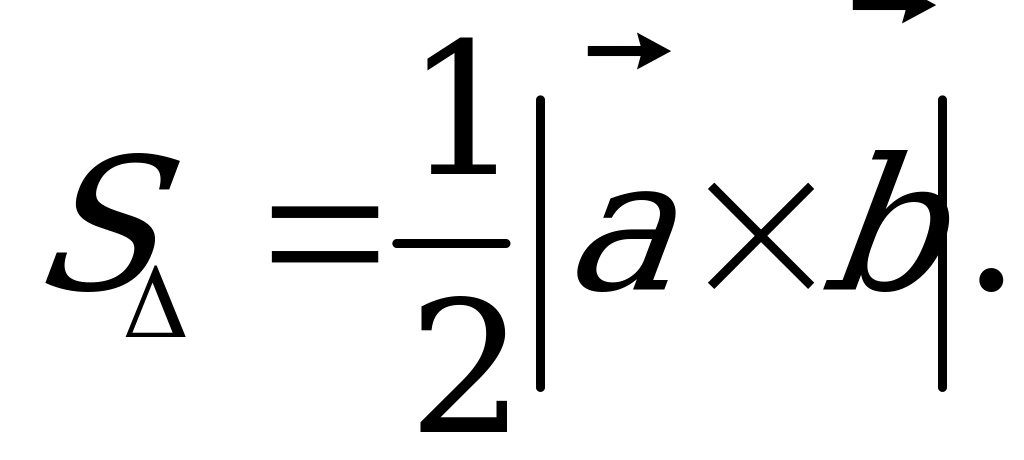
WEKTORLARYŇ GARYŞYK KÖPELTMEK HASYLY
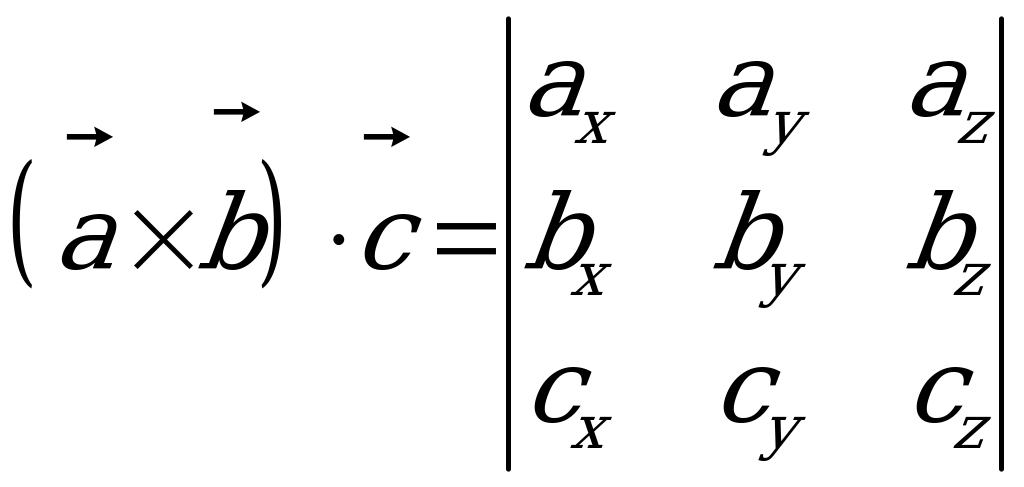 .
.






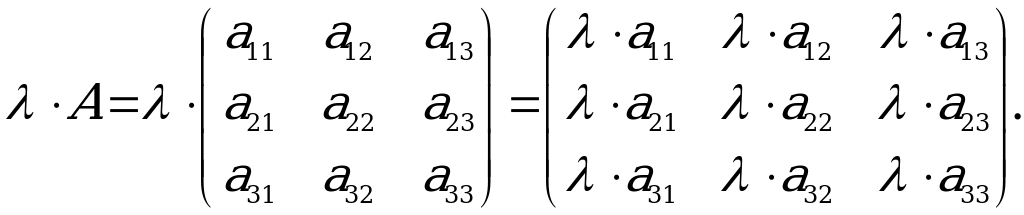
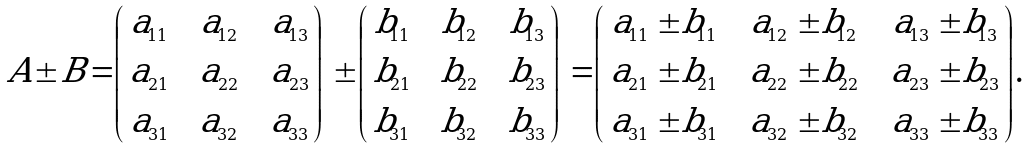
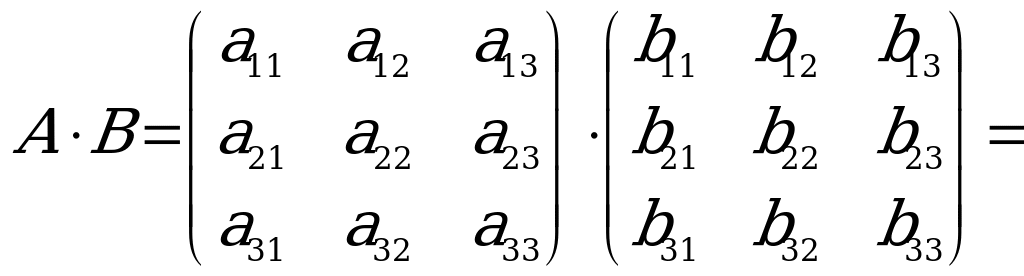


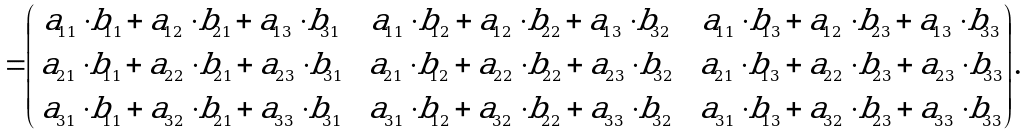
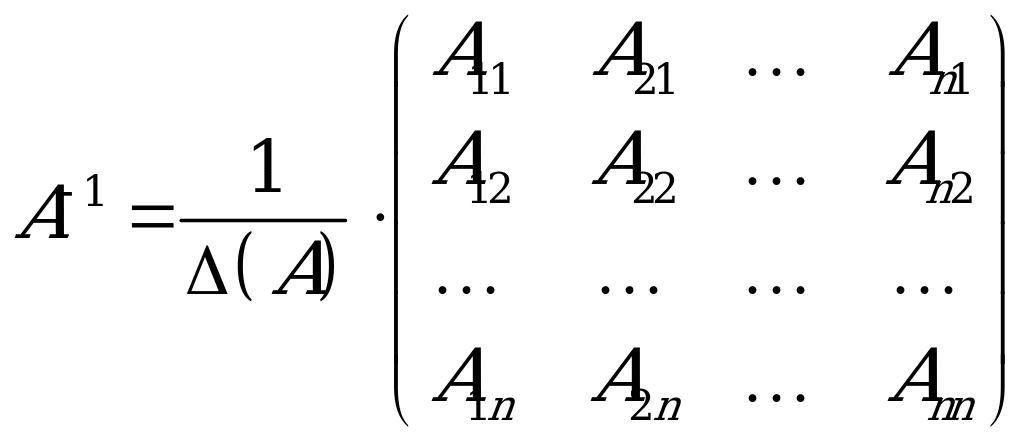
 ESGITLEÝJILERIŇ HASAPLANYŞY
ESGITLEÝJILERIŇ HASAPLANYŞY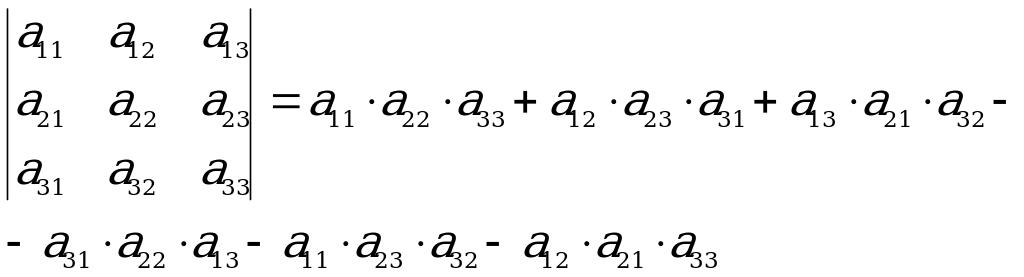
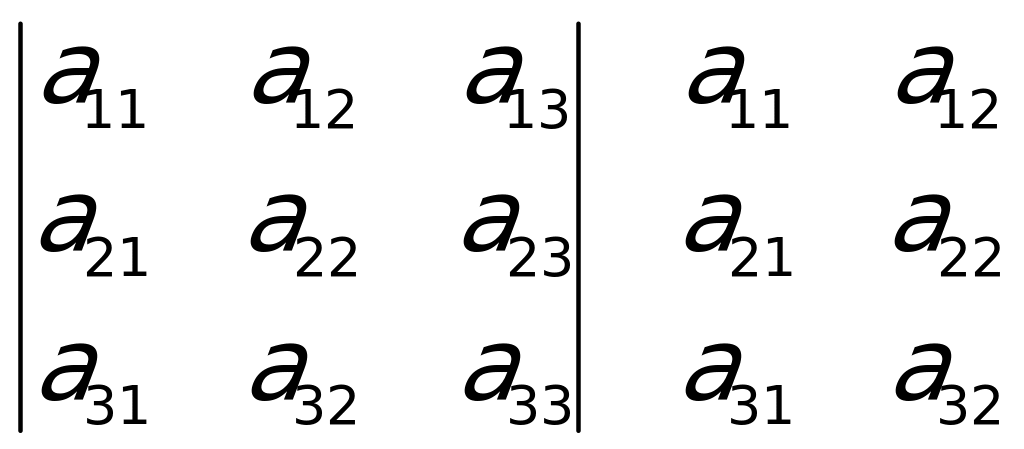
 .
.  .
.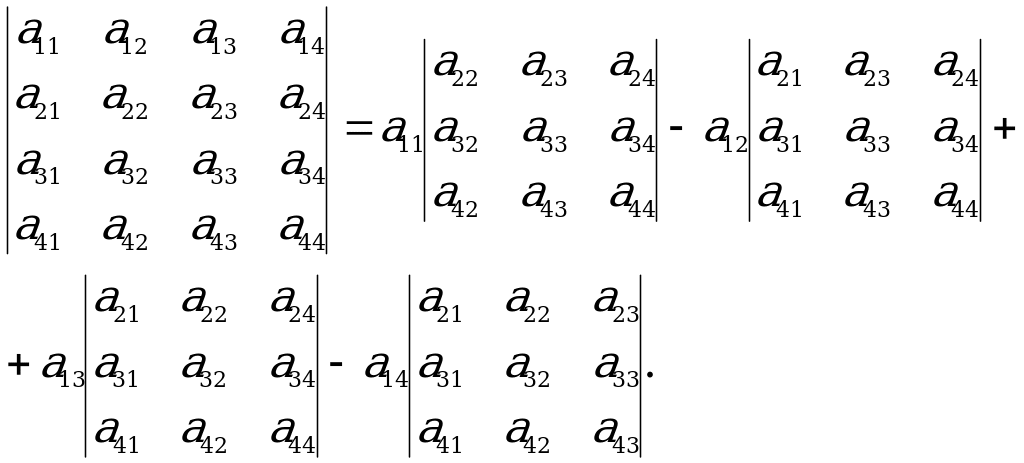

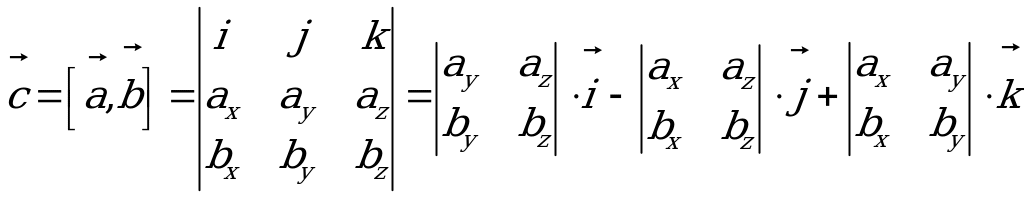
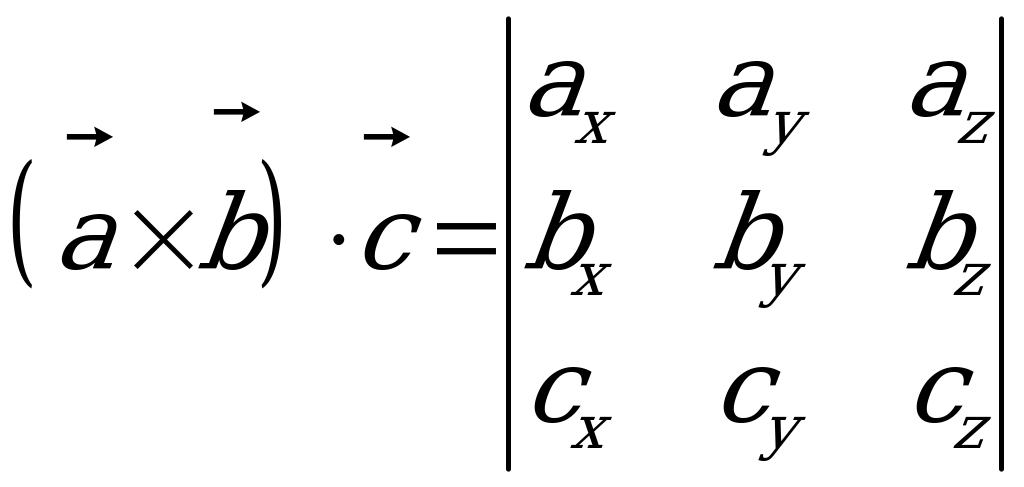 .
. 









