Осевая и центральная симметрии

Тема урока:

Осевая и центральная симметрии

Учитель :Любимцева Ольга Николаевна ,

учитель математики

МБОУ СОШ № 2 им А.С Пушкина

Нижегородской области, г. Арзамас,

2015

«Симметрия  устанавливает забавное и удивительное сродство между предметами, явлениями и теориями, внешне, казалось бы, ничем не связанными: земным магнетизмом, женской вуалью ... »

Дж. Ньюмен

«Симметрия является той идеей, посредством которой человек на протяжении веков пытался постичь и создать порядок, красоту и совершенство»

Г. Вейль

Симметрия - (от греч. symmetry) - соразмерность, постоянство, пропорциональность.

Симметрия -  соразмерность,   одинаковость  в расположении частей чего-нибудь по противоположным сторонам от точки, прямой или плоскости.  ( толковый словарь русского языка Ожегова)

Симметрия - пропорциональность,   соразмерность  в расположении частей целого в пространстве, полное  соответствие  (по расположению, величине) одной половины целого  другой  половине.

( толковый словарь Ушакова)

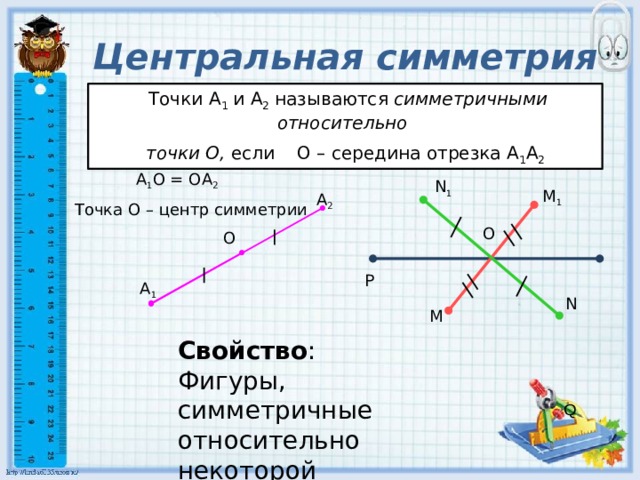
Центральная симметрия

Точки А 1 и А 2 называются симметричными относительно

точки О, если О – середина отрезка А 1 А 2

А 1 О = ОА 2

Точка О – центр симметрии

N 1

M 1

А 2

О

О

Р

А 1

N

M

Свойство :

Фигуры, симметричные

относительно некоторой

точки, равны.

Q

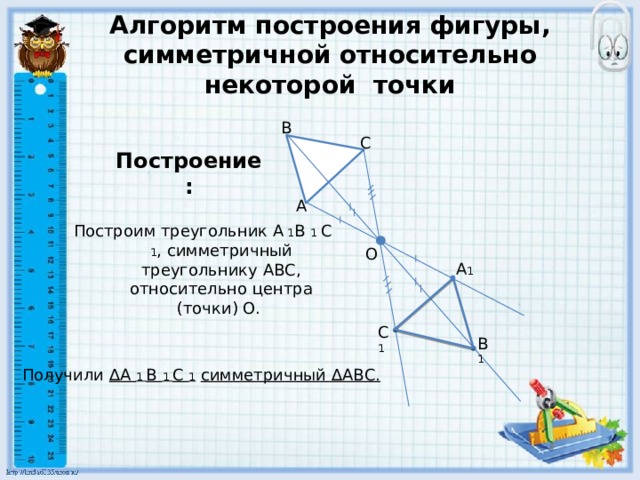
Алгоритм построения фигуры, симметричной относительно некоторой точки

В

Построение:

С

А

Построим треугольник А 1 В 1 С 1 , симметричный треугольнику АВС, относительно центра (точки) О.

О

А 1

С 1

В 1

Получили ∆А 1 В 1 С 1 симметричный ∆АВС.

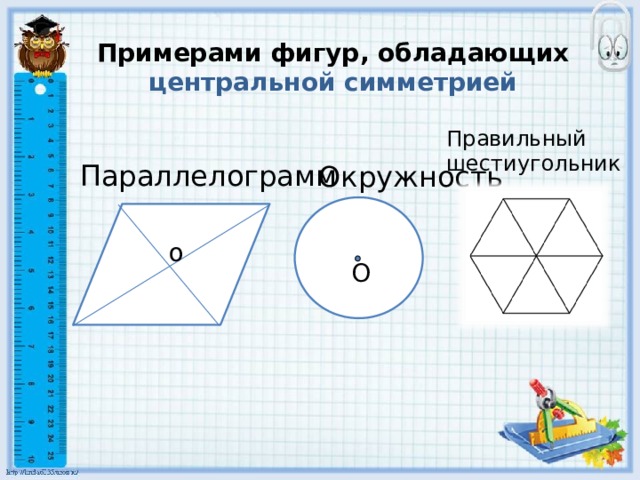
Примерами фигур, обладающих центральной симметрией

Правильный

шестиугольник

Параллелограмм

Окружность

о

О

Симметричность на координатной плоскости

y

y

A

A 1

A

B

B 1

B

C

D

C

C 1

x

x

D 1

C 1

B 1

A 1

Центральная симметрия

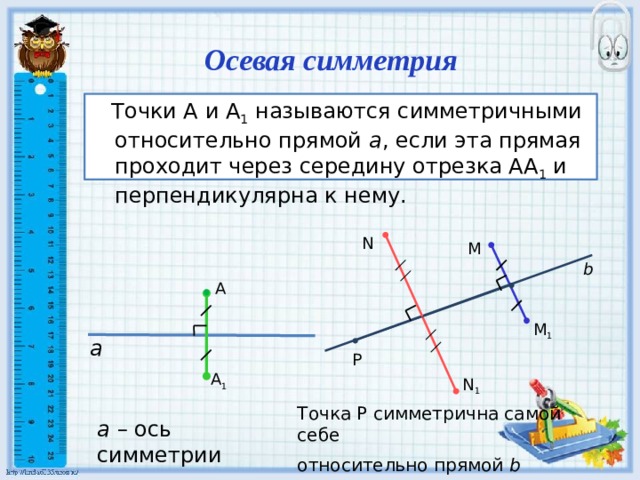
Осевая симметрия

Точки А и А 1 называются симметричными относительно прямой а , если эта прямая проходит через середину отрезка АА 1 и перпендикулярна к нему.

N

М

b

А

М 1

а

Р

А 1

N 1

Точка Р симметрична самой себе

относительно прямой b

а – ось симметрии

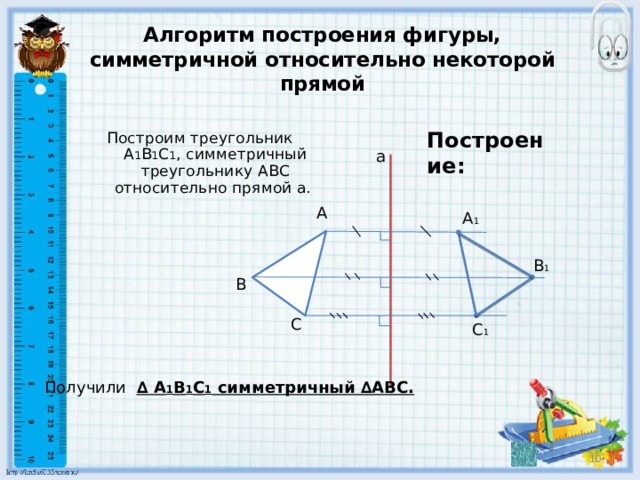
Алгоритм построения фигуры, симметричной относительно некоторой прямой

Построение:

Построим треугольник А 1 В 1 С 1 , симметричный треугольнику АВС относительно прямой а.

а

А

А 1

В 1

В

С

С 1

Получили ∆ А 1 В 1 С 1 симметричный ∆АВС.

Задание:

Постройте слово, симметричное относительно прямой а.

У р о к

а

Решение

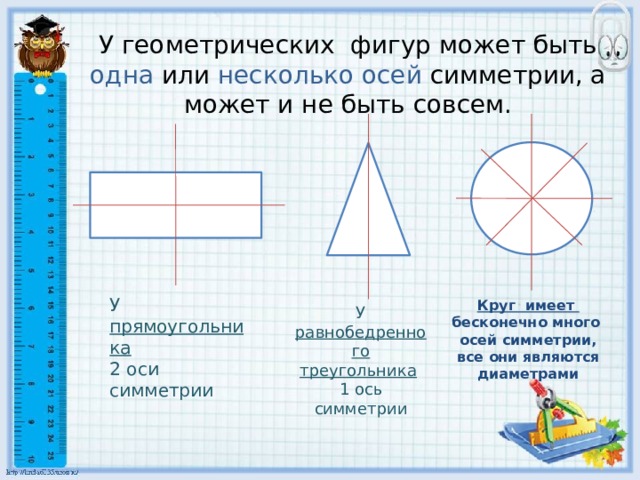
У геометрических фигур может быть одна или несколько осей симметрии, а может и не быть совсем.

Круг имеет бесконечно много

У прямоугольника

2 оси симметрии

осей симметрии,

все они являются диаметрами

У равнобедренного треугольника

1 ось симметрии

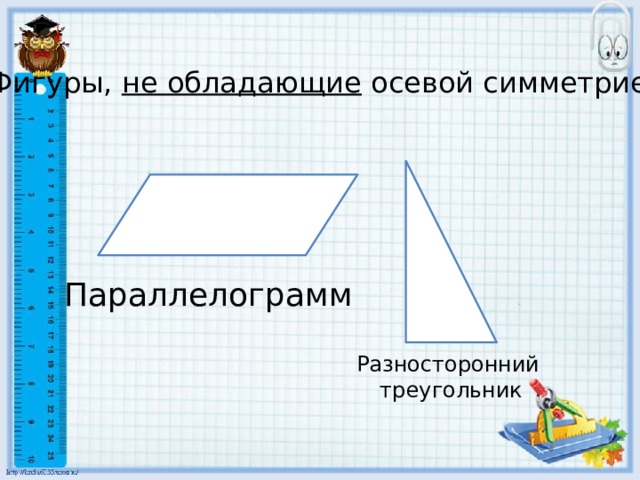
Фигуры, не обладающие осевой симметрией

Параллелограмм

Разносторонний

треугольник

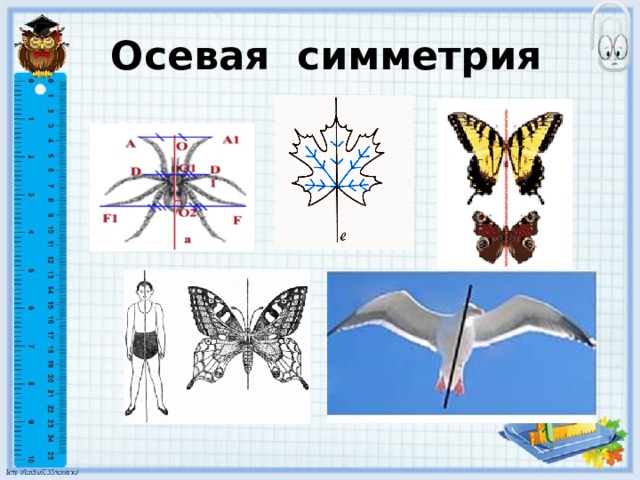
Осевая симметрия

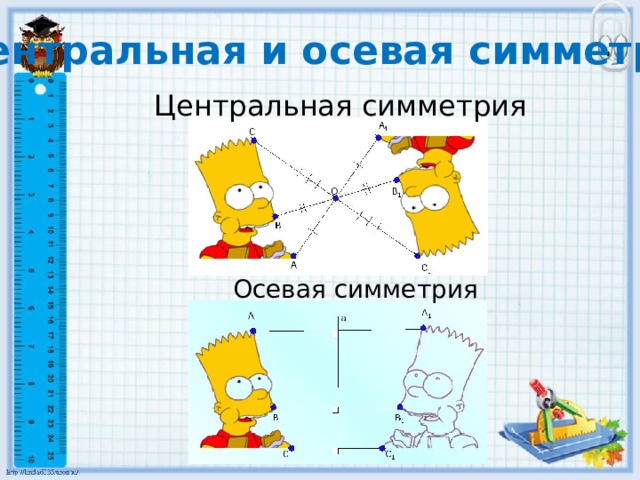
Центральная и осевая симметрия

Центральная симметрия

Осевая симметрия

Симметрия вокруг нас

Симметрия вокруг нас.

Какие из букв А, Б, Г, Е, Х, И, М, Н, О, Т, Я имеют:

а) центр симметрии

Х, И, Н, О

б) ось симметрии

А, Е, Х, М, Н, О, Т

Закрепление изученного материала

№ 418 (устно),

№ 422 (устно),

№ 416,

№ 421.

Домашнее задание:

Вопросы 16 – 20 стр. 115,

№ 421, № 419, № 423