Основные определения и теоремы по функциональному анализу
Определение: Элемент наилучшего приближения – L – линейное многообразие, плотное в E. xE u: ║x-u║
Теорема: Для любого элемента нормированного пространства существует хотя бы один элемент наилучшего приближения из конечномерного подпространства.
Теорема: Для элемента из строго нормированного конечномерного пространства существует единственный элемент наилучшего приближения из конечномерного подпространства.
Теорема: Рисса о существовании почти ортогонального элемента. E-НП LE, (0,1) zE\L ║z║=1 (z,L)1-
Определение: Полное нормированное пространство - любая фундаментальная последовательность сходиться.
Теорема: О пополнении нормированного пространства. Любое нормированное пространство можно считать линейным многообразием, плотным в некотором полном нормированном пространстве.
Определение: Гильбертово пространство – нормированное пространство, полное в норме, порожденной скалярным произведением.
Теорема: Для любого элемента гильбертова пространства существует единственный элемент наилучшего приближения в конечномерном подпространстве гильбертова пространства.
Определение: L плотное в E, если xE uL: ║x-u║
Теорема: Чтобы L было плотно в H ортогональное дополнение к L состояло только из нулевого элемента.
Определение: Сепарабельное – нормированное пространство, содержащее некоторое счетное плотное в нем множество.
Определение: Ортогональное дополнение – множество элементов ортогональных к элементам данного пространства.
Определение: Линейный оператор – отображение, для которого A(ax+by)=aAx+bAy
Определение: Непрерывный оператор – AxAx0 при x x0
Определение: (X,Y) – пространство линейных операторов
Теорема: Пусть X и Y – полные НП и A – непрерывен на некотором подпространстве пространства X, тогда он непрерывен на всем X.
Определение: Ограниченный оператор - ║x║≤1 с: ║Ax║≤c
Теорема: A – ограниченный xX ║Ax║≤c║x║
Теорема: Для того чтобы А был непрерывен чтобы он была ограничен
Теорема: {An} равномерно ограничена {An}- ограничена.
Теорема: {Anx} – ограниченно {║An║}- ограничена.
Определение: Сильная (равномерная) сходимость ║An-A║0, n, обозначают AnA
Определение: Слабая сходимость - xX ║(An-A)x║Y0, n
Теорема: Для того, чтобы имела место сильная сходимость {An} сходилась равномерно на замкнутом шаре радиуса 1
Теорема: Банаха-Штенгауза AnA n слабо 1) {║An║}- ограничена 2) AnA, x’X, x’=x
Теорема: Хана Банаха. A:D(A)Y, D(A)X A’:XY 1) A’x=Ax, xD(A) 2) ║A’║=║A║
Определение: Равномерная ограниченность - a x: ║x(t)║≤a
Определение: Равностепенная непрерывность t1,t2 : ║x(t1)-x(t2)║
Теорема: (X,Y) полное, если Y – полное.
Определение: Ядро – {xX | Ax=0}
Определение: Сопряженное пространство – пространство функционалов X*:=(X,E)
Определение: Сопряженный оператор A*: Y*X*
Теорема: Банаха A:XY и X,Y- полные нормированные пространства. Тогда A-1 и ограничен.
Определение: Оператор А – обратимый
Определение: Оператор А- непрерывнообратимый если 1) A- обратим, 2) R(A)=Y, 3) A-1-ограничен.
Теорема: A-1 и ограничен m0 xX ║Ax║≥m║x║
Теорема: Рисса о представлении линейного функционала в гильбертовом пространстве. Пусть f:XY – линейный ограниченный функционал ! yH xH f(x)=(x,y)
Определение: MX называется бикомпактным, если из любой ограниченной последовательности можно выделить сходящуюся к элементам этого же множества последовательность.
Определение: Множество называется компактным, если любая ограниченная последовательность элементов содержит фундаментальную подпоследовательность.
Теорема: Хаусдорфа. MX компактно 0 конечная -сеть
Теорема: Арцела. MC[a,b] компактно все элементы множества равномерно ограничены и равностепенно непрерывны.
Определение: Компактный (вполне непрерывный) оператор – замкнутый шар пространства X переводит в замкнутый шар пространства Y.
Определение: (X,Y) – подпространство компактных операторов
Теорема: Шаудера. A(X,Y) A*(X*,Y*)
Линейные нормированные пространства
Пространства векторов
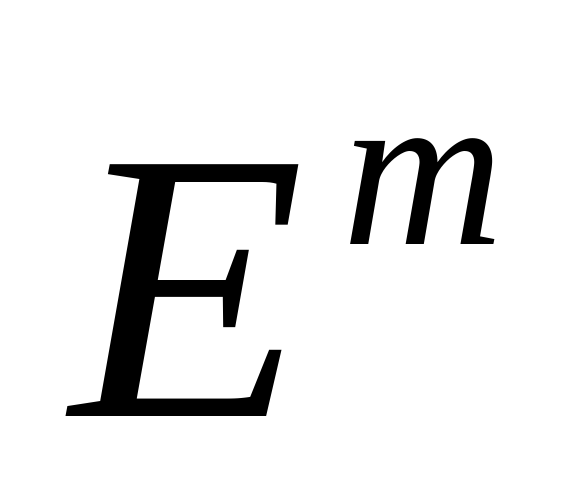
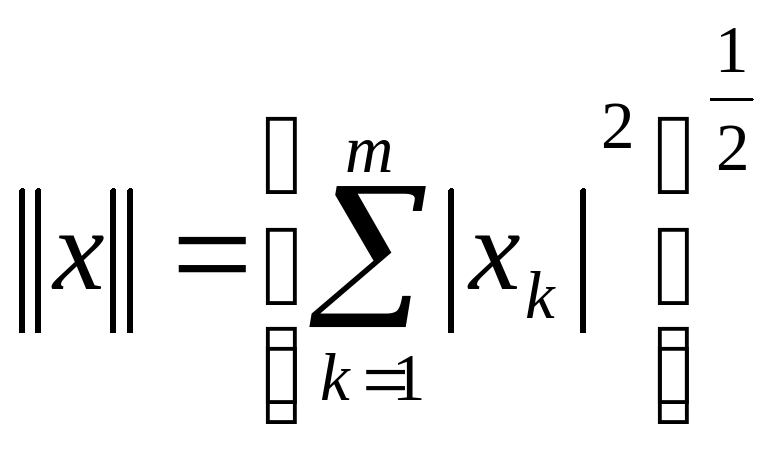 сферическая норма
сферическая норма
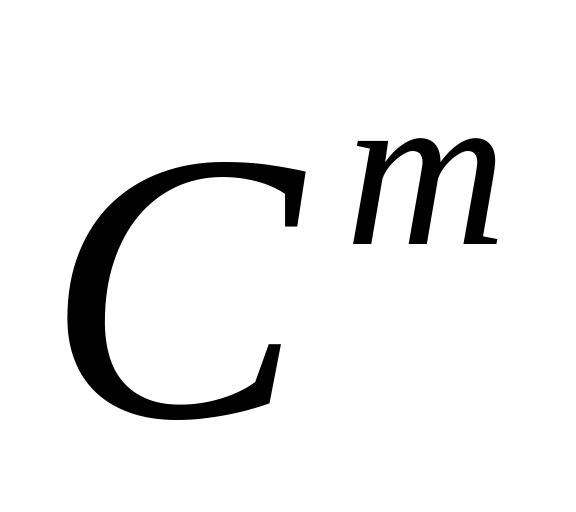
 кубическая норма
кубическая норма

 ромбическая норма
ромбическая норма
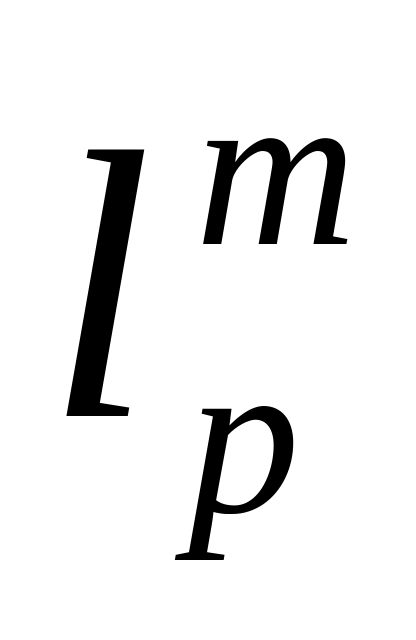
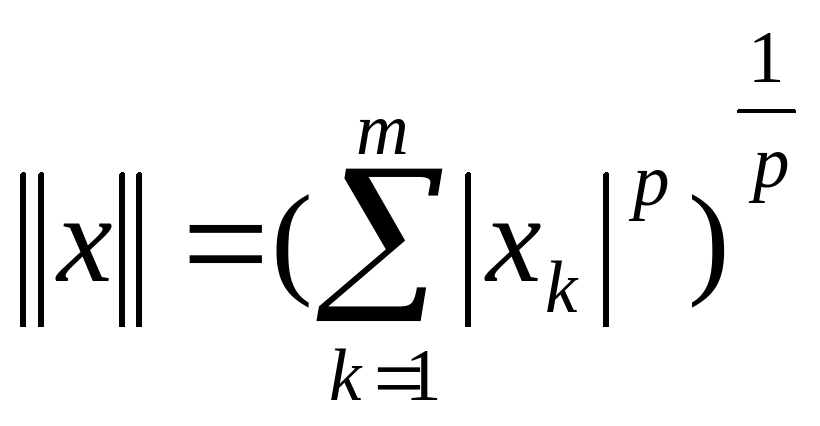 p1
p1
Пространства последовательностей 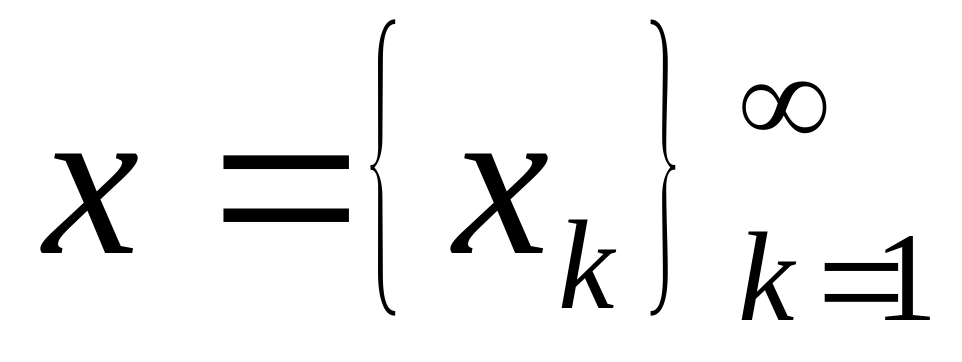

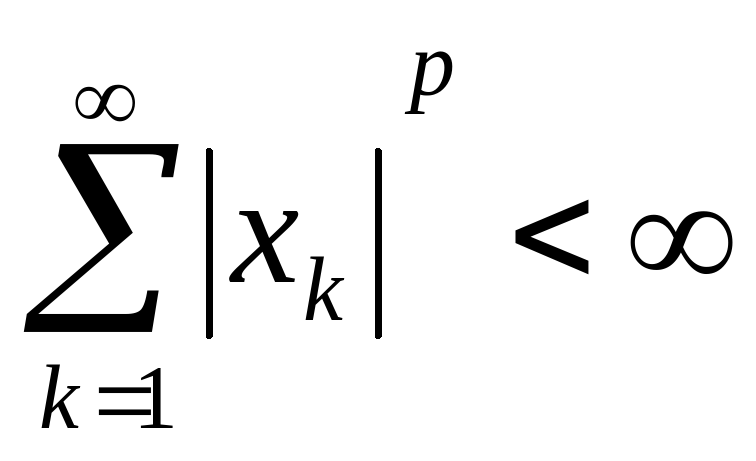
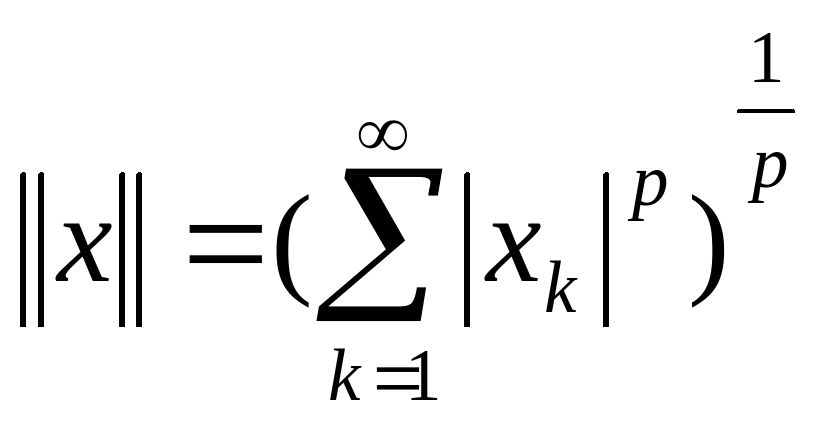 p1
p1
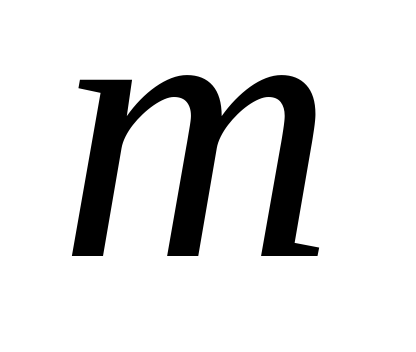 или
или 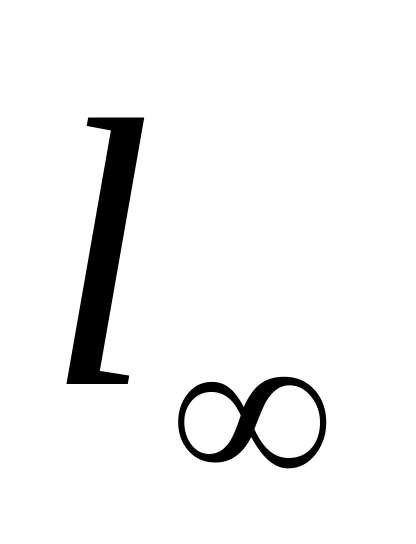 пространство ограниченных последовательностей
пространство ограниченных последовательностей
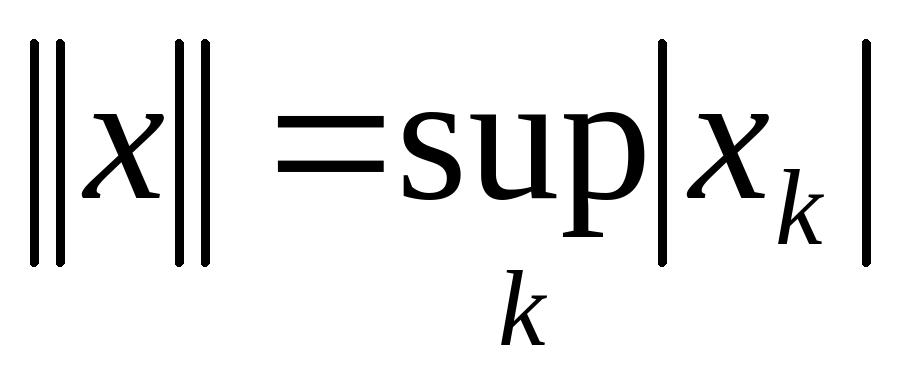
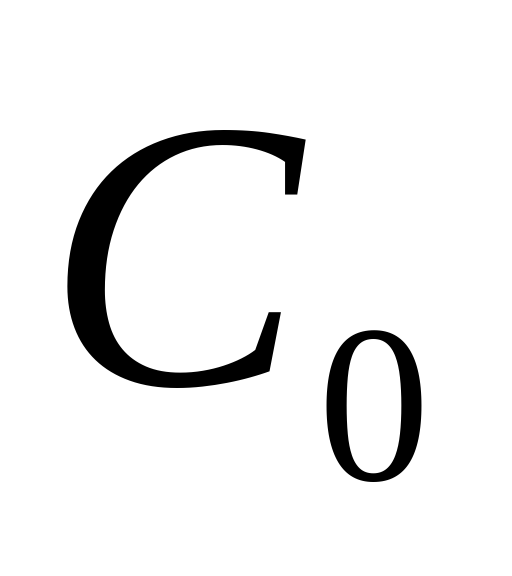 пространство последовательностей, сходящихся к нулю
пространство последовательностей, сходящихся к нулю
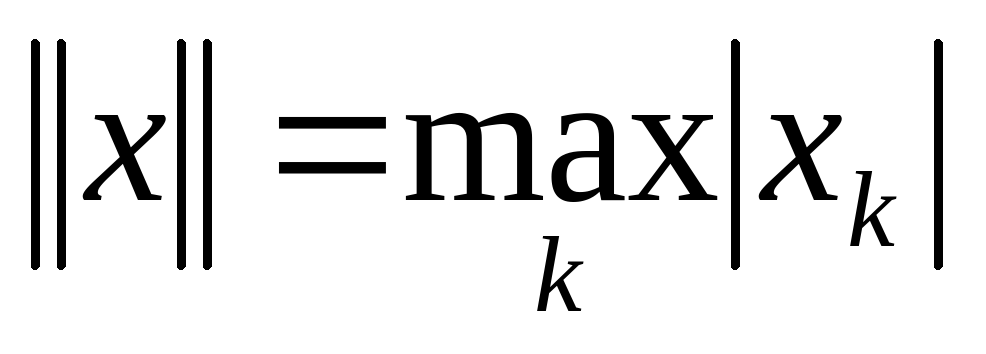
 пространство сходящихся последовательностей
пространство сходящихся последовательностей
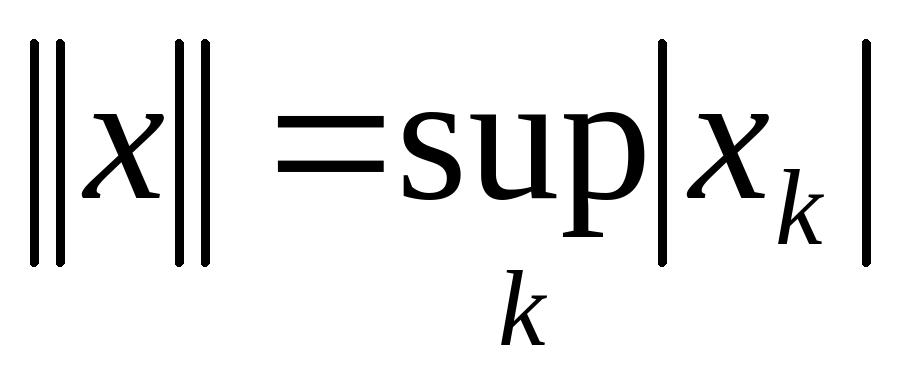
Пространства функций
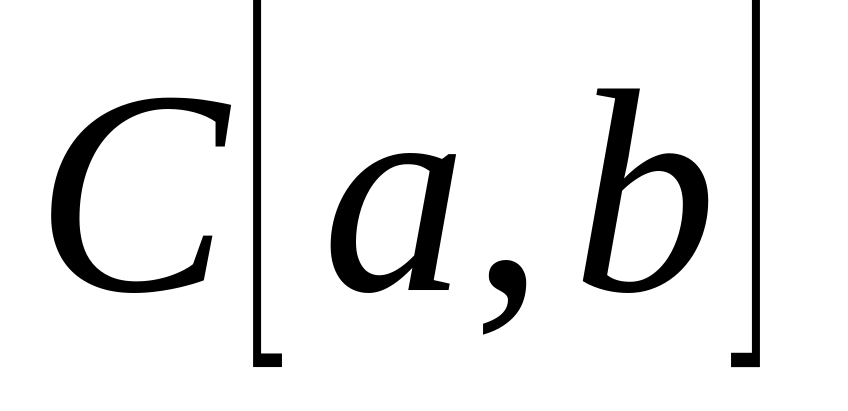 пространство непрерывных на
пространство непрерывных на 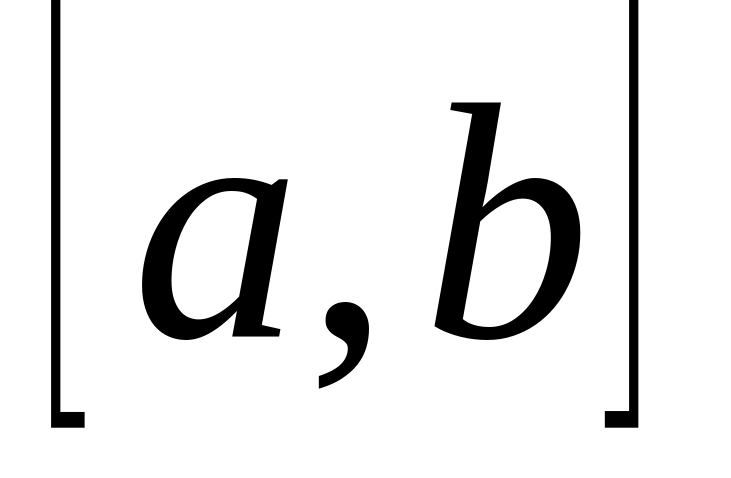 функций
функций
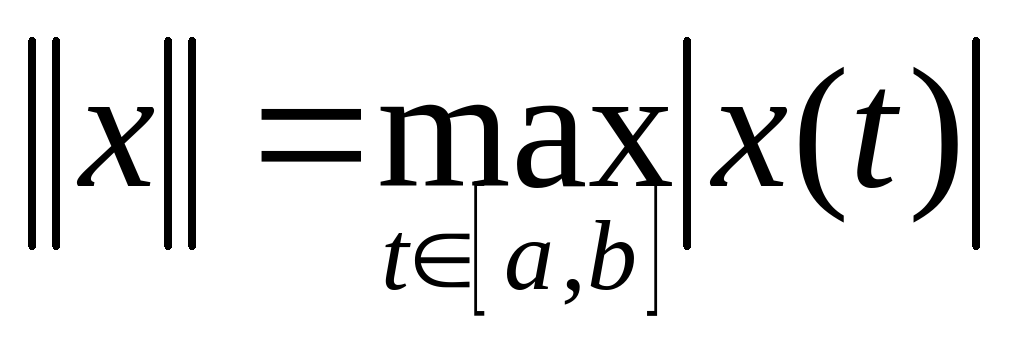
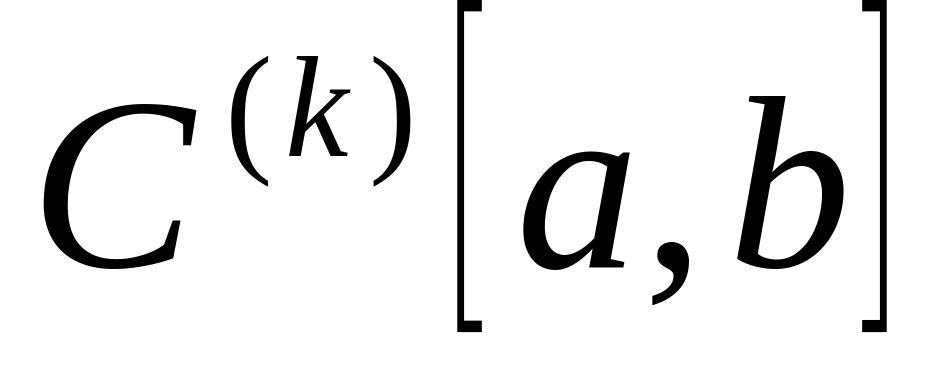 пространство k раз непрерывно дифференцируемых на
пространство k раз непрерывно дифференцируемых на 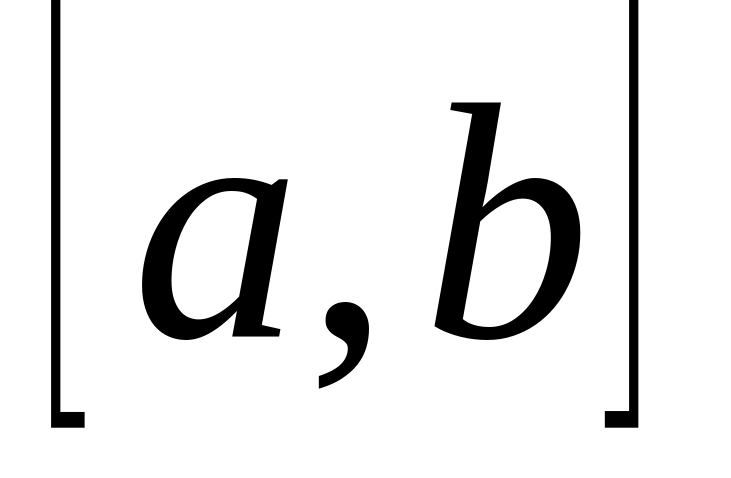 функций
функций
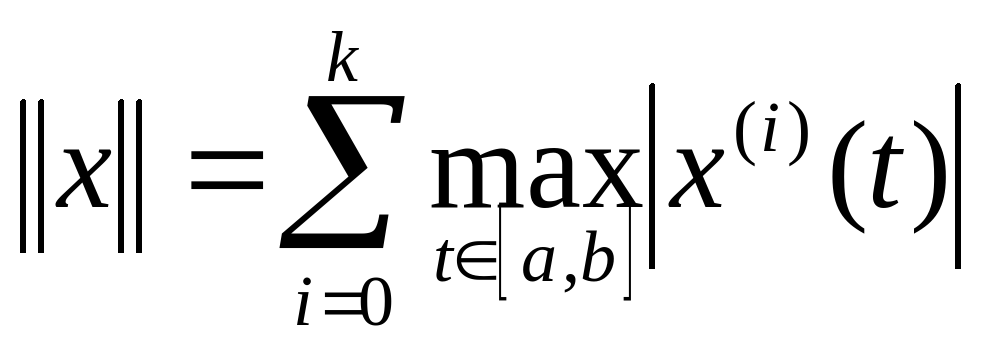
Јp[a,b] пространство функций, интегрируемых в степени p (не Гильбертово)
- пополнение Јp[a,b] (Гильбертово)
Неравенство Гёльдера p,q0
Неравенство Минковского







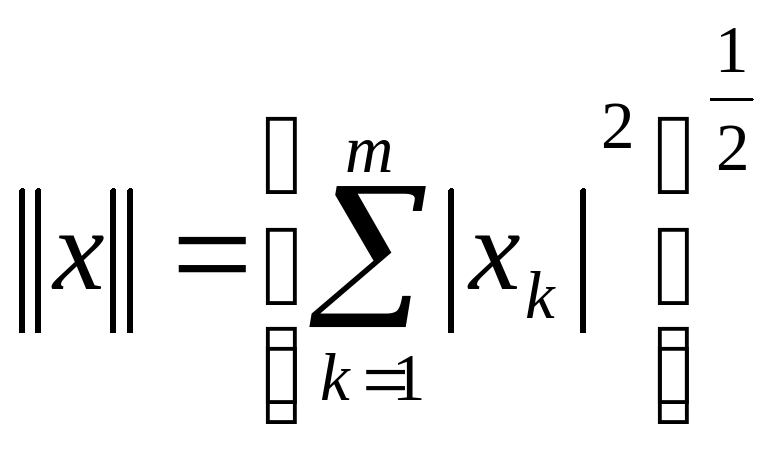 сферическая норма
сферическая норма









