ГОСУДАРСТВЕННОЕ АВТОНОМНОЕ ПРОФЕССИОНАЛЬНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
НОВОСИБИРСКОЙ ОБЛАСТИ
«БАРАБИНСКИЙ МЕДИЦИНСКИЙ КОЛЛЕДЖ»
Рассмотрено на заседании ЦМК ОГСЭД
Протокол № ____от________________
Председатель_____________________

МЕТОДИЧЕСКАЯ РАЗРАБОТКА
ТЕОРЕТИЧЕСКОГО ЗАНЯТИЯ ДЛЯ ПРЕПОДАВАТЕЛЯ
Специальность 31.02.01 Лечебное дело
Дисциплина ЕН.02. «Математика»
Раздел 3. Основные понятия и методы теории вероятностей и математической статистики
Тема 3.1. Основные понятия дискретной математики. Множества
Разработчик: преподаватель Потемкина О.А.
 2021
2021
СОДЕРЖАНИ
Методический лист 3
Примерная хронокарта занятия 6
Исходный материал 7
Задания для закрепления и систематизации знаний 15
Критерии оценки 18
Контролирующий материал 19
Эталоны ответов 20
Критерии оценки 20
Задание для самостоятельной внеаудиторной работы студентов 20
Список использованных источников 21
Выписка из рабочей программы дисциплины ЕН.02. «Математика»
по специальности 31.02.01 Лечебное дело
| Наименование разделов и тем | Содержание учебного материала, лабораторные и практические работы, самостоятельная работа обучающихся, курсовая работа (проект) | Объем часов | Уровень освоения |
| 1 | 2 | 3 | 4 |
| Раздел 3. | Основные понятия и методы теории вероятностей и математической статистики | 36 |
|
| Тема 3.1. Основные понятия дискретной математики. Множества | Содержание учебного материала | 2 |
| Роль и место математики в современном мире. Значение математики в профессиональной деятельности при организации диспансеризации населения и участии в её проведении. Числовые множества, действия с множествами. Способы задания множеств. Дискретное множество. Решение прикладные задач в области профессиональной деятельности. | 1,2 |
| Лабораторные работы | ‑ |
|
| Практические работы | ‑ |
| Контрольные работы | ‑ |
| Самостоятельная работа обучающихся Работа с учебником [1, стр. 244-251], повторение материала; Выполнение упражнений [1, стр. 277, задание №107]. | 1 |
Методический лист
Тип занятия – урок обобщения и систематизации знаний
Вид занятия – комбинированное занятие
Продолжительность – 90 мин.
Слайд 2
Цели занятия
1. Учебные цели:
сформировать знание о значении математики в профессиональной деятельности и при освоении профессиональной образовательной программы;
способствовать формированию умения решать прикладные задачи в области профессиональной деятельности;
2. Развивающие цели:
способствовать развитию у студентов ОК 1. Понимать сущность и социальную значимость своей будущей профессии, проявлять к ней устойчивый интерес;
способствовать развитию у студентов ОК 3.Принимать решения в стандартных и нестандартных ситуациях и нести за них ответственность.
3. Воспитательные цели:
способствовать развитию ОК 2. Организовывать собственную деятельность, выбирать типовые методы и способы выполнения профессиональных задач, оценивать их эффективность и качество.
Методы обучения – объяснительно-иллюстративный, репродуктивный, частично-поисковый.
Место проведения занятия – аудитория колледжа.
Мотивация
Математические методы широко применяются в медицине.
В медицинских образовательных учреждениях роль математики неприметна, поскольку во всех случаях на первый план, естественно, выдвигаются медицинские и клинические дисциплины, а теоретические, в том числе математика, отодвигаются на задний план, не учитывая, что математизация здравоохранения в мировом пространстве происходит стремительно, вводятся новые технологии и методы, основанные на математических достижениях в области медицины.
В последние годы активное внедрение в медицину методов математического моделирования и создание автоматизированных, в том числе и компьютерных, систем существенно расширило возможности диагностики и терапии заболеваний.
Математика принадлежит к числу тех дисциплин общеобразовательного блока, которые имеют большие возможности для развития личности. В силу специфики своего содержания данная дисциплина формирует способность к усвоению новой информации, умение планировать и адекватно оценивать свои действия, развивает силу и гибкость ума, способность к аргументации способствовать развитию у студентов ОК 1. Понимать сущность и социальную значимость своей будущей профессии, проявлять к ней устойчивый интерес; ОК 2. Организовывать собственную деятельность, выбирать типовые методы и способы выполнения профессиональных задач, оценивать их эффективность и качество.
Что изучает дискретная математика?
Со школьной скамьи нам известно, что некоторые явления в окружающем мире можно описать с помощью понятий действительного числа и непрерывного трехмерного пространства. Математические модели раскрывают многие закономерности материального мира.
Дискретная математика – сравнительно новое направление в математике, объединяющее отдельные ее разделы, ранее сформированные как самостоятельные теории. К ним относятся математическая логика и теории множеств, графов.
Дискретный анализ – самостоятельный раздел современной математики, изучающий свойства различных структур, имеющих конечный характер. Они могут возникать как в самой математике, так и в ее приложениях. К их числу принято относить объекты, имеющие прерывный (дискретный) характер в отличие от объектов, изучаемых классической математикой и носящих непрерывный характер.
Несмотря на то, что отдельные направления дискретной математики зародились в глубокой древности и совершенствовались параллельно с классической математикой, наиболее интенсивно дискретная математика стала развиваться в последнее столетие. В настоящее время знание дискретной математики необходимо специалистам в различных областях деятельности.
Дискретная математика изучает объекты, которые порой не имеют ни физической, ни числовой интерпретации. В классической математике характеристики реальных объектов можно представить в виде чисел, а закономерности – в виде соотношений. В отличие от реальных характеристиками информационных объектов могут служить понятия «структура», «отношение», «связь». Обычно объекты информатики рассматривают как комбинации некоторых абстрактных символов, над которыми производятся некие манипуляции.
Объектом исследования дискретной математики являются дискретные множества – совокупность, набор некоторых элементов. Поэтому начнем с самого общего глубоко абстрактного раздела этой науки – теории множеств и отношений, которая стала интенсивно развиваться с внедрением вычислительной техники. Примерная хронокарта занятия
| № | Наименование этапа | Время | Цель этапа | Деятельность | Оснащение |
| преподавателя | студентов |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Организационный этап | 1 | Мобилизовать внимание студентов на работу, привить дисциплинированность, аккуратность. | Отмечает отсутствующих студентов в журнале. Сообщает тему и план занятия. | Староста называет отсутствующих студентов. | Журнал |
| Мотивационный этап и целеполагание | 3 | Раскрыть теоретическую и практическую значимость темы, повысить интерес к профессии. Способствовать развитию у студентов ОК 1. Понимать сущность и социальную значимость своей будущей профессии, проявлять к ней устойчивый интерес; | Объясняет студентам важность изучения данной темы, озвучивает цели занятия | Слушают, задают вопросы, записывают новую тему | Методическая разработка теоретического занятия, мультимедийная презентация |
| Изложение исходной информации | 40 | Формировать знание о значение математики в профессиональной деятельности и при освоении профессиональной образовательной программы; Формировать умение решать прикладные задачи в области профессиональной деятельности; | Излагает новый материал | Записывают материал, задают вопросы, решают задачи | Приложение 1 Мультимедийная презентация |
| Выполнение заданий для закрепления знаний | 30 | Закрепить умение решать прикладные задачи.. Способствовать развитию у студентов ОК 3.Принимать решения в стандартных и нестандартных ситуациях и нести за них ответственность. | Инструктирует и контролирует выполнение заданий, обсуждает правильность ответов | Выполняют задания, слушают правильные ответы после выполнения, вносят коррективы | Приложение 2 Мультимедийная презентация |
| Предварительный контроль знаний | 15 | Оценить эффективность занятия. Способствовать развитию у студентов ОК 3.Принимать решения в стандартных и нестандартных ситуациях и нести за них ответственность. | Инструктирует и проводит контроль | Выполняют задания | Приложение 3 |
| Задание для самостоятельной внеаудиторной работы студентов | 0,5 | Формировать и закреплять знания. Способствовать развитию у студентов ОК 3.Принимать решения в стандартных и нестандартных ситуациях и нести за них ответственность, ОК 2. Организовывать собственную деятельность, выбирать типовые методы и способы выполнения профессиональных задач, оценивать их эффективность и качество. | Дает задание для самостоятельной внеаудиторной работы студентов, инструктирует о правильности выполнения | Записывают задание | Мультимедийная презентация +МР |
| Подведение итогов занятия | 0,5 | Развивать эмоциональную устойчивость, дисциплинированность | Оценивает работу группы в целом. Объявляет оценки, мотивирует студентов, выделяет наиболее подготовленных | Слушают, участвуют в обсуждении, задают вопросы | Журнал |
Исходный материал
План
Множества
Изображение множеств
Основные операции над множествами
Свойства операций над множествами
Круги Эйлера
Слайд 3
Множества
Сегодня на занятии мы систематизируем имеющиеся со школы представления об универсальном языке теории множеств, познакомимся с видами множеств и отношений между ними, узнаем, как сравнивать конечные и бесконечные множества и как подсчитывать число их элементов.
Общие понятия теории множеств
Язык теории множеств. Множество – одно из основных понятий современной математики, с которым каждый человек знаком со школьной скамьи. «Множество решений уравнения или неравенства», «множество точек на плоскости», «множество действительных чисел» и т.д. – привычные словосочетания, не требующие дополнительных рассуждений и определений.
? Что же такое множество?
Понятия множество, элементы множества – первичные базисные неопределяемые понятия, на которых строится теория множеств.
Множество ‑ совокупность элементов, объединенных некоторым признаком, свойством.
Например, множество книг в библиотеке, множество студентов в группе, множество натуральных чисел N и т.д.
Запись а М означает: элемент а принадлежит множеству М, т.е. элемент а обладает некоторым признаком множества М.
Аналогично а М читаем как: элемент а не принадлежит множеству М.
Слайд 4
Множество считается заданным, если или перечислены все его элементы, или указано свойство, которым обладают те и только те элементы, которые принадлежат данному множеству.
Первый вариант будем записывать так: М = {т1, т2, тk }, например, М= {0, 1}.
Последний вариант будем записывать так: М= {b|Р(b)}.
Такая запись читается как: М состоит из тех (всех) элементов b, которые обладают признаком Р.
Например, М = {п|п N, n М составляют только те натуральные числа, что меньше пяти.
Само свойство P будем называть характеристическим. В качестве характеристического свойства может выступать указанная для этого свойства порождающая процедура, которая описывает способ получения элементов нового множества из уже полученных элементов или из других объектов. Тогда элементами множества считаются все объекты, которые могут быть получены с помощью этой процедуры.
Например, множество М2n = {1, 2, 4, 8, 16, 32, ...} всех чисел, являющихся неотрицательными степенями числа 2. Можно задать с помощью порождающей функции М2n = {2i Z, i ≥ 0}.
Запись М = {х|Р(х)} означает: множество М состоит из всех элементов х, обладающих признаком Р.
Например, запись М = {х|х3 + 3х2 + 2х = 0} означает, что множество М содержит только корни данного уравнения, т.е. числа {0; -1; -2}.
Запись Z= {X| |OX| ≤ 4} означает, что для любых X расстояние OX меньше или равно 4, т.е. множество всех точек, для которых расстояние до Х не больше 4, есть шар с центром в точке О и радиусом R = 4.
Запись A = {х| х ≥ 7, х N} читается так: для любых натуральных х, начиная с 7.
Отметим, что в записи М = {х| Р(х)} переменная х является «немой», т.е. несущественной: от нее ничего не зависит. Можно было бы употребить любую другую букву, например у, и все равно это было бы «множество всех элементов, обладающих признаком P», а как называть элементы – несущественно: главное, чтобы они обладали признаком.
Если множество не содержит элементов, обладающих характеристическим признаком, то оно называется и обозначается .
Например, множество целых решений неравенства 5 х является пустым: K ={х | х Z, 5 .
Пустым будет множество действительных решений уравнений х2 + 25 = 0 и 52x-3 =-1.
Множество, не являющееся пустым, называется непустым.
? Всегда ли удается, соблюдая все правила, задать множество
? Например, как задать множество всех множеств
? Будет ли такое множество содержать себя как отдельный элемент (по указанному характеристическому свойству оно должно содержать все возможные множества, а значит, и себя?)
Слайд 5
Изображение множеств
Множества удобно изображать с помощью кругов Эйлера (диаграмм Венна). Элементы множества изображаются точками внутри круга, если они принадлежат множеству (а М), и точками вне круга, если они множеству не принадлежат (b М). Будем также использовать символы х вместо слов «для любых х», «каждый элемент х» и х вместо слов «существует х».
Из множества М можно выделить его часть (также выделением нового характеристического свойства или перечислением элементов) – множество К, все элементы которого обладают таким же признаком, как и элементы множества М. Множество К называют подмножеством множества М и обозначают К М.
Более строго: множество К называется подмножеством множества М (К М), если для любого х М выполняется х М (т.е. x К влечет х М.
Например, добавляя к множеству однозначных целых чисел А = {0, 1,… 9} признак «число делится на 3», получаем множество В = {0, 3, 6, 9} А.
Так, множество целых чисел Z является подмножеством множества рациональных чисел Q. Для числовых множеств справедливо соотношение: N Z Q R C, где N – множество натуральных чисел, Q – рациональных, R – действительных, С – комплексных чисел. Для любого непустого множества М можно сразу указать два его подмножества независимо от состава и структуры М: это оно само и пустое. Очевидно, пустое множество содержится (является подмножеством) в любом множестве.
Также необходимо учитывать различие в употреблении знаков включения () и принадлежности () для множества множеств.
Например, М – множество всех отделений в нашем колледже, а К – отделение «Лечебное дело». Хотя К само является множеством (состоит из студентов и сотрудников – преподавателей, администрации и др.), верна запись К М, так как отделение К является элементом всего множества М. Запись К М неверна, так как множества К и М содержат разные элементы: К – людей, М – отделения. Однако, если рассмотрим множество О – совокупность людей со всех отделений (например, при всеобщем голосовании по насущному вопросу), то, безусловно, К О.
Универсальным называют множество U, состоящее из всех возможных элементов, обладающих данным признаком.
Например, множество планет Солнечной системы U = {Земля, Марс, Венера, Юпитер, Сатурн, Уран, Плутон, Меркурий, Нептун). Заметим, что понятие универсального множества четко не определено, т.е. некорректно. U можно включить в другое множество W, и оно тоже будет универсальным.
Например, долго считалось, что множество действительных чисел R универсально (т.е. описывает всю математику), пока не открыли поле комплексных чисел С и надкомплексные числа и не поняли, что не существует универсального числового множества. Тем не менее, там, где область объектов не выходит за рамки некоего множества, иногда бывает удобно оперировать с этим термином. Ведь ржаное поле – вселенная для мыши.
Равными называют два множества А и В, состоящие из одинаковых элементов: А = В.
Например, равны множества решений уравнений 4х - 8 = 16, х/15 = 2/5 и
5х–3 = 125, так как их решением является одно и то же число 6.
Равны множества букв, из которых составлены слова «навес» и «весна». Равны множества корней уравнения х2 = 1 и множество М {(-1)k / k=0, 1, 2, ...}. Поэтому задача «решить уравнение», знакомая с детства, в реальности означает «решить уравнение в каком-то множестве».
Так, уравнение х2 + 1 = 0 не имеет действительных корней:
{х| x2 + 1 = 0, х R} = 0, но имеет два комплексных корня х = i, х= -i: {х| х2 + 1 = 0, х С} = {i, -i}.
Равенство двух множеств А и В означает также, что А В и В А.
И наоборот, выполнение свойств А В и В А означает выполнение равенства А = В. Эти утверждения равносильны.
Число элементов множества А называется мощностью множества и обозначается |А| или п(А). Так, мощность пустого множества равна 0: п() = 0, а мощность множества планет Солнечной системы n(U) = 9 или |U| = 9.
Слайд 6
Основные операции над множествами
Из данных множеств А и В можно построить новые множества с помощью операций объединения, пересечения, вычитания и др..
Таблица 1
Основные операции над множествами
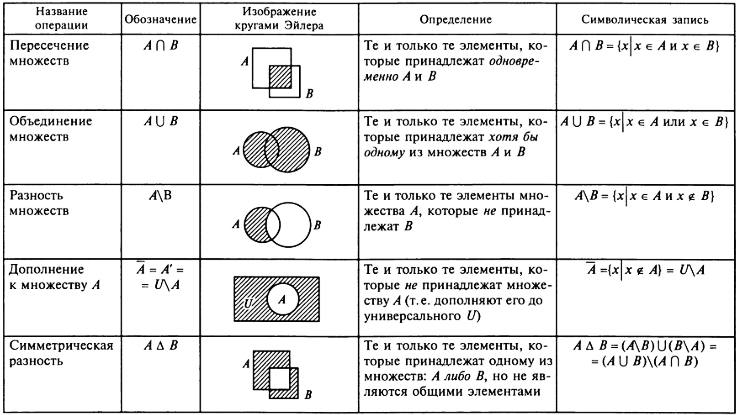
Например.
Пусть А = {а, b, с, g, е}, В = {а, с, e, f, r, т}, тогда АUВ = {а, b, c, g, e, f, r, m}, АUВ = {а, с, е), A∩B = {b, g}, В\А = = {f,r,m}, A Δ B = {b, g, f, r, т}.
Обратим внимание, что для разности двух множеств не выполняется переместительный закон: А\В В\А. Это становится очевидным, если одно множество пустое (например, А), а другое – непустое.
Слайд 7
Свойства операций над множествами
Операции над множествами обладают рядом свойств, похожих на свойства операций сложения и умножения чисел. Рассмотрим законы, справедливые для любых множеств А, В, С
1. AUB=BUA, A∩B= В∩А – переместительный закон (коммутативность) для операций объединения и пересечения. Поскольку это свойство справедливо для любого конечного числа множеств, то удобно использовать знаки U и ∩ для обозначения объединения и пересечения многих множеств.
Например, 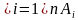 означает объединение п множеств вне зависимости от того, какое из них считать первым, вторым и т.д.
означает объединение п множеств вне зависимости от того, какое из них считать первым, вторым и т.д.
2. (AUB) U C= AU (BUC), (А∩В) ∩С = А∩ (В∩С) - сочетательный закон (ассоциативность) для операций объединения и пересечения.
3. (A U B) ∩ C = (A∩C) U (B∩ С) – распределительный закон (дистрибутивность) пересечения относительно объединения множеств.
4. (A∩B) U С = (AU С) ∩(BU С) – распределительный закон объединения относительно пересечения множеств.
5. AUA = A, A∩A = А, А (АUВ) – законы поглощения.
6. U=' и = U', т.е. универсальное и пустое множества являются дополнениями друг друга.
7. Если обозначить через Аi все подмножества А1, А2, А3, Аn множества А, то будут справедливы равенства: A= и A\
и A\  =
= .
.
Операция дополнения обладает рядом характерных свойств.
8. Для любого множества X U справедливо X' = (X')' = X.
9. Для любых двух множеств X и Y справедливо: если X U, Y U, то (Х ∩ Y)' = Х' U Y' или (X U Y)' = Х' ∩ Y'.
10. Множество А можно разбить на классы непересекающихся подмножеств Ai если:
объединение всех подмножеств совпадает с множеством А: A=
пересечение любых двух различных подмножеств пусто, т.е. для любых i j выполняется Ai∩ Aj= .
Рассмотрим примеры.
1. Произвольное множество А разбивается на два дополняющих друг друга подмножества А1 и А2 = A\A1 , таких, что А1 U А2 = А и А1 ∩ А2 = .
2. Множество двузначных чисел U = {10, 11, 12, .... 98, 99} можно разбить на классы по признаку остатка от деления на 4: класс, порожденный остатком 0: А0 = {12, 16, 20, .... 96}. Аналогично А1 = {13, 17, 20, ...,97}; А2 = {10, 14, 18, ...,98}; А3 = {11, 15, 19, 99}.
Разбиение на классы используется для классификации объектов. Так, множество квартир дома может быть разбито на подмножество квартир отдельных подъездов, а множество квартир каждого подъезда – на подмножество квартир одного этажа.
Слайд 8
Круги Эйлера. Задачи на пересечение или объединение множеств
Это новый тип задач, в которых требуется найти некоторое пересечение множеств или их объединение, соблюдая условия задачи.
Круги Эйлера – геометрическая схема, с помощью которой можно изобразить отношения между подмножествами, для наглядного представления.
Метод Эйлера является незаменимым при решении некоторых задач, а также упрощает рассуждения. Однако, прежде чем приступить к решению задачи, нужно проанализировать условие. Иногда с помощью арифметических действий решить задачу легче.
Рассмотрим несколько задач, решаемых с помощью теории множеств.
Задача 1. Пятьдесят лучших студентов колледжа наградили за успехи поездкой в Англию и Германию. Из них 5 не владели ни одним разговорным иностранным языком, 34 знали английский язык и 27 – немецкий. Сколько студентов владели двумя разговорными иностранными языками?
Решение. Введем обозначения множеств:
Е – множество студентов, не владеющих ни одним иностранным языком;
А – множество всех студентов, А= 50;
В – множество студентов, владеющих английским языком, В = 34;
С – множество студентов, владеющих немецким языком, С = 27;
D – множество студентов, владеющих английским и немецким языками, D = х.
Представим множества графически с помощью кругов Эйлера.
Слайд 9
С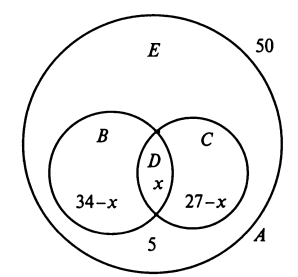 пособ 1. Составим уравнение: 34 -x+27-x + x+5 = 50, откуда х= 16.
пособ 1. Составим уравнение: 34 -x+27-x + x+5 = 50, откуда х= 16.
Способ 2. Найдем D из уравнения В+С– D = А – 5 или
34 + 27 – х = 50 - 5, отсюда х = 16.
Следовательно, 16 студентов свободно общались на двух иностранных языках.
Слайд 10
Задача 2. Каждый студент группы программистов занимается в свободное время либо в НСО, либо спортом.
С колько студентов в группе, если 23 увлекаются спортом, 12 занимаются в НСО, а 7 совмещают занятия в НСО и увлечение спортом?
колько студентов в группе, если 23 увлекаются спортом, 12 занимаются в НСО, а 7 совмещают занятия в НСО и увлечение спортом?
Решение. Изобразим множества кругами Эйлера, обозначив множества «спортсменов» – А и «исследователей» – В.
Тогда n(А∩\В) = 7, n(А) = 23, n(В) = 12;
n(А U В) = n(А) + n(В) – n(А ∩ В) = 23 + 12 – 7 = 28.
Итак, в группе 28 студентов.
Слайд 11
Задача 3. Из 35 студентов, побывавших на каникулах в Москве, все, кроме двоих, делились впечатлениями. О посещении Большого театра с восторгом вспоминали 12 человек, Кремля – 14, а 16 – о концерте, по три студента запомнили посещение театра и Кремля, а также театра и концерта, а четверо – концерта и пребывания в Кремле. Сколько студентов сохранили воспоминания одновременно о театре, концерте и Кремле?
Решение.
Введем обозначения:
А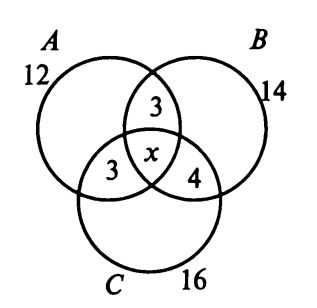 – множество студентов, вспоминающих о театре, n(А) = 12;
– множество студентов, вспоминающих о театре, n(А) = 12;
В – о Кремле, n(В) = 14; С – о концерте, n(С) = 16;
D – множество всех студентов, побывавших в поездке.
Изобразим множества графически с помощью кругов Эйлера.
n(AUBUC) = n(А) + n(В) + n(С) - n(А∩В) – n(А∩С) – n(B∩C) + n(A∩B∩C).
Обозначим n(A∩B∩C) = х, тогда 35 – 2 = 12 + 14 + 16 – 3 – 3 – 4 + х, отсюда х = 3.
Всего 3 студента рассказывали о трех культурных мероприятиях поездки.
Приложение 2
Задания для закрепления и систематизации знаний
Слайд 12-13
Примечание: примеры а, б, в – выполняются устно, г, д, е – письменно.
1. Укажите множество действительных чисел, соответствующее записи:
 г)
г) 
б) 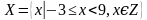 д)
д) 
в)  е)
е) 
Эталоны ответов
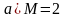 г)
г) 
б)  д)
д) 
в)  е)
е) 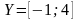
Слайд 14
Задание выполняется устно
2. Дано множество  .
.
1. Какие из элементов этого множества являются множествами?
2. Какие из следующих записей верны:
а) 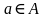 б)
б)  в)
в) 
г)  д)
д)  е)
е) 
Эталоны ответов
1) 
2) верны утверждения под буквами а, г, д
Слайд 15
Задание выполняется письменно
3. Дано множество Мi:
а) г)
б) д)
в) е)
1. Приведите по три примера элементов множества Мi.
2. Укажите, каким из множеств, принадлежат числа 3, 4, 5, 13, 25, 
3. Запишите эти утверждения символически.
Эталоны ответов
1)
а)  г)
г)
б) д)
в) е)
2), 3)
3, 4, 13  ,
, ;
;
5 ; 25
; 25 ;
; 
 ;
;

 ;
; 
 ;
;
Слайд 16
Задание выполняется устно
4. Приведите по три примера конечных и бесконечных множеств.
Задание выполняется письменно
5. Составьте 10 различных новых слов из букв слова:
а) стационар
б) ратификация
1. Представьте буквы новых слов в виде множеств и найдите мощность множеств, состоящих из кортежей длины n, где п≥5.
2. Какое слово, полученное из букв данного, имеет наибольшую длину?
3. Найдите новое слово, состоящее из всех тех букв, которые входят в данное слово.
Задание выполняется письменно
Слайд 17
6. Даны множества А1 = {a, b,c}; A2 = {c, d, e, f}; U = {a, b, c, d, e, f}. Осуществите над множествами А1 и A2 операции: а) объединения; б) пересечения; в) разности; г) дополнения.
Эталоны ответов
а) А1 A2 ={a, b, c, d, e, f}
б) А1 A2 ={c}
в) А1 \ A2 ={a, b}
г) U\ А1 ={d, e, f}, U\ A2 = {a, b}
Задание выполняется письменно
7. Даны множества А = {1,3}; В = {2, 3, 4}; С= {2,4}, U = {1, 2, 3, 4}.
Найти: а)  б)
б)  ; в)
; в)  ; г)
; г) 
Эталоны ответов
а)  = { 2, 4}{1} = {1, 2, 4}
= { 2, 4}{1} = {1, 2, 4}
б)  =
=  = {1, 2, 4}
= {1, 2, 4}
в)  ={1,3}{1} = (1}
={1,3}{1} = (1}
г)  = {3} {1,3} = {1,3}
= {3} {1,3} = {1,3}
Слайд 18
Задание выполняется устно
8. Пусть универсальное множество U – множество всех учащихся и преподавателей некоторого техникума; А – множество всех преподавателей; В – множество учащихся, успевающих по всем дисциплинам на «отлично»; С – множество неуспевающих учащихся; D – множество учащихся в группе №1.
Каков содержательный смысл каждого из следующих множеств:
а)  (Ответ: множество всех учащихся техникума (без преподавателей));
(Ответ: множество всех учащихся техникума (без преподавателей));
б)  (Ответ: множество преподавателей и учащихся, кроме, успевающих по всем предметам на «отлично»);
(Ответ: множество преподавателей и учащихся, кроме, успевающих по всем предметам на «отлично»);
в)  (Ответ: множество отличников, обучающихся в группе №1);
(Ответ: множество отличников, обучающихся в группе №1);
г) D\C (Ответ: множество учащихся группы №1, справляющихся с учебным планом);
д)  (Ответ: множество преподавателей и всех успевающих учащихся;
(Ответ: множество преподавателей и всех успевающих учащихся;
е)  (Ответ: множество преподавателей и отличников из группы №1);
(Ответ: множество преподавателей и отличников из группы №1);
ж) С\D (Ответ: множество неуспевающих учащихся всех групп, кроме первой).
Слайд 19
Задание выполняется письменно
9. Даны отрезки .
Найдите следующие множества и изобразите их на числовой прямой:
а)  б)
б)  в)
в) 
Эталоны ответов
а)  б)
б)  в)
в) 
Слайд 20
Задание выполняется устно
10. Определите мощность множества:
а)  б) {0};
б) {0};
в) состоящего из букв слова «математика»;
г) состоящего из букв слова «перпендикулярные»;
д) состоящего из цифр числа 635252;
е) состоящего из цифр числа 1010111.
Эталоны ответов
а)  ; б) 1; в) 5; г) 11; д) 4; е) 2.
; б) 1; в) 5; г) 11; д) 4; е) 2.
Слайд 21
Задания 10- 15 выполняется письменно
Задание: найдите решение задачи
11. Некоторые ребята из нашего класса любят ходить в кино. Известно, что 15 ребят смотрели фильм «Обитаемый остров», 11 человек – фильм «Стиляги», из них 6 смотрели и «Обитаемый остров», и «Стиляги». Сколько человек смотрели только фильм «Стиляги»?
Слайд 22
12. Среди школьников шестого класса проводилось анкетирование по любимым мультфильмам. Самыми популярными оказались три мультфильма: «Белоснежка и семь гномов», «Губка Боб Квадратные Штаны», «Волк и теленок». Всего в классе 38 человек. «Белоснежку и семь гномов» выбрали 21 ученик, среди которых трое назвали еще «Волк и теленок», шестеро – «Губка Боб Квадратные Штаны», а один написал все три мультфильма. Мультфильм «Волк и теленок» назвали 13 ребят, среди которых пятеро выбрали сразу два мультфильма. Сколько человек выбрали только один мультфильм «Губка Боб Квадратные Штаны»?
Слайд 23
13. В пионерском лагере 70 ребят. Из них 27 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов; 3 спортсмена посещают и драмкружок и хор. Сколько ребят не поют, не увлекаются спортом, не занимаются в драмкружке? Сколько ребят заняты только спортом?
Слайд 24
14. Из 100 ребят, отправляющихся в детский оздоровительный лагерь, кататься на сноуборде умеют 30 ребят, на скейтборде – 28, на роликах – 42. На скейтборде и на сноуборде умеют кататься 8 ребят, на скейтборде и на роликах – 10, на сноуборде и на роликах – 5, а на всех трех – 3. Сколько ребят не умеют кататься ни на сноуборде, ни на скейтборде, ни на роликах?
Эталоны ответов
11. 5
12. 8
13. 19 (ничем не увлекаются), 5 занимаются только спортом
14. 29
Критерии оценки
«5» –студент дал не менее 5 верных ответов при выполнении устных/письменных упражнений первым или работал у доски самостоятельно и достиг верного результата;
«4» – студент дал не менее 4 верных ответов при выполнении устных/письменных упражнений первым или работал у доски частично самостоятельно (с наводящими вопросами) и достиг верного результата;
«3» – студент работал у доски, но верный результат был достигнут только с помощью преподавателя.
Приложение 3
Задания для предварительного контроля знаний
Контролирующий материал
| 1 вариант | 2 вариант |
| 1. Расположите заданные множества в порядке возрастания количества их элементов. 1) пустое множество; 2) 2,4,6,8,10}; 3) xN 1≤x≤3}; 4) множество целых чисел.
2. Даны множества: А=1,2,3,4,8,12}, В=0,2,4,6,8,10}. Установите соответствие между следующими множествами и необходимыми для их получениями над множествами А и В. 1. 2,4,8} А) объединение множеств А и В; 2. 0,1,2,3,4,6,8,10,12} Б) пересечение множеств А и В; 3. 1,3,12} В) разность множеств А и В.
3. Найдите: если множества А={7, 8, 9}, В={8, 9}
4. В магазин «Мир музыки» пришло 35 покупателей. Из них 20 человек купили новый диск певицы Максим, 11 – диск Земфиры, 10 человек не купили ни одного диска. Сколько человек купили диски и Максим, и Земфиры? | 1. Выберите утверждение о числовых множествах, которое является истинным … 1) Множество целых чисел является подмножеством множества рациональных чисел. 2) Число 0 принадлежит множеству натуральных чисел. 3) Множество натуральных чисел является подмножеством иррациональных чисел.
2. Даны два множества: А=3,5,10,21}, В=–5,0,10,12}. Их пересечением является … 1) пустое множество; 2) –5,0,3,5,10,12,21}; 3) число 10; 4) число 0.
3. Найдите: если множества А={1, 2}, В={3, 4};
4. На полке стояло 26 волшебных книг по заклинаниям, все они были прочитаны. Из них 4 прочитал и Гарри Поттер, и Рон. Гермиона прочитала 7 книг, которых не читали ни Гарри Поттер, ни Рон, и две книги, которые читал Гарри Поттер. Всего Гарри Поттер прочитал 11 книг. Сколько книг прочитал только Рон? |
Слайд 22
Эталоны ответов | 1 вариант | 2 вариант |
|
 ; ;
1-Б, 2-А, 3-В; 1) {7, 8, 9} 2) {8, 9} 3) {7}; 6. |
 ; ;
3; 1) {1, 2, 3, 4} 2) {} 3) {1, 2}; 8 |
Критерии оценки
«5» –все ответы совпадают c эталоном;
«4» – дано три верных ответа;
«3» – дано два верных ответа;
«2» – дано менее двух верных ответов.
Слайд 25
Задание для самостоятельной внеаудиторной работы студентов
Работа с учебником [1, стр. 244-251], повторение материала;
Решение задач:
В отделе института работают несколько человек. Каждый из них знает хотя бы один иностранный язык, причем: 6 знают немецкий, 6 – английский, 7 – французский, 4 – английский и немецкий, 3 – немецкий и французский, 2 – французский и английский, 1 – все три языка. Сколько всего человек работает в отделе? Сколько из них знают только английский?
Из 35 учащихся класса 20 посещают математический кружок, 11 – физический, 10 – не посещают кружки. Сколько учеников посещают математический и физический кружки одновременно, сколько – только математический?
Эталоны ответов
10 человек работают в отделе, 0 – знают только английский
6 человек посещают математический и физический кружки одновременно, 14 человек – только математический
Критерии оценки
«5» –все ответы совпадают c эталоном и представлено развернутое решение;
«4» – дано одно верное решение и представлено развернуто;
«3» – дано одно верное решение, но при ответе допускает ошибки;
«2» – задание не выполнено.
Слайд 26
Список использованных источников
Гилярова, М. Г. Математика для медицинских колледжей: учебник. – Ростов н/Д: Феникс, 2019. – 457 с.: ил. – (Среднее медицинское образование).
Михеев, В.С. Математика: учеб. пособие [Текст] / В.С. Михеев [и др.]; под ред. Н.М. Демина. –Ростов н/Д : Феникс, 2009. – 896 с. – (Среднее профессиональное образование).
1








 2021
2021
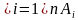 означает объединение п множеств вне зависимости от того, какое из них считать первым, вторым и т.д.
означает объединение п множеств вне зависимости от того, какое из них считать первым, вторым и т.д. и A\
и A\  .
. пособ 1. Составим уравнение: 34 -x+27-x + x+5 = 50, откуда х= 16.
пособ 1. Составим уравнение: 34 -x+27-x + x+5 = 50, откуда х= 16.  колько студентов в группе, если 23 увлекаются спортом, 12 занимаются в НСО, а 7 совмещают занятия в НСО и увлечение спортом?
колько студентов в группе, если 23 увлекаются спортом, 12 занимаются в НСО, а 7 совмещают занятия в НСО и увлечение спортом?  – множество студентов, вспоминающих о театре, n(А) = 12;
– множество студентов, вспоминающих о театре, n(А) = 12;  г)
г) 
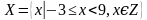 д)
д) 
 е)
е) 
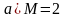 г)
г) 
 д)
д) 
 е)
е) 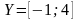
 .
. 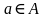 б)
б) 
















