Дата проведения:
Тема урока: Основные тригонометрические тождества.
Тип урока: урок усвоения новых знаний
ЦЕЛИ УРОКА:
1)ОБРАЗОВАТЕЛЬНАЯ: вывод формул зависимости между синусом, косинусом и тангенсом одного и того же угла (числа); обучение применению этих формул для вычисления значений синуса, косинуса, тангенса числа по заданному значению одного из них.
2)РАЗВИВАЮЩАЯ: учить анализировать, сравнивать, строить аналогии, обобщать и систематизировать, доказывать и опровергать, определять и объяснять понятия..
3)ВОСПИТАТЕЛЬНАЯ: воспитание добросовестного отношения к труду и положительного отношения к знаниям.
ДИДАКТИЧЕСКОЕ ОБЕСПЕЧЕНИЕ УРОКА: учебник, тетрадь, плакаты по теме урока, таблицы.
Литература: А.Н.Колмогоров; А.Ш.Алимов
ХОД УРОКА
1. Организационный момент: приветствие, проверка явки учащихся, заполнение журнала.
2. Проверка готовности учащихся к уроку: настрой учащихся на работу, доведение до них плана урока.
3. Новая тема: Рассмотрим точку В(х;у), лежащую на тригонометрической окружности . Она получена поворотом точки А(1;0) вокруг начала координат на угол  .
.
Синусом угла  является ордината точки В(х;у). Косинусом угла
является ордината точки В(х;у). Косинусом угла является её абсцисса.
является её абсцисса.

Рисунок 1 – точка В на тригонометрической окружности
Образовался прямоугольный треугольник ОВС. По теореме Пифагора 
Катет ОС - это абсцисса точки В или  , катет ВС- её ордината, или
, катет ВС- её ордината, или а гипотенуза ОВ - радиус единичной окружности, ОВ=1.Получаем формулу:
а гипотенуза ОВ - радиус единичной окружности, ОВ=1.Получаем формулу:
 (1)
(1)
В тригонометрии её называют основным тригонометрическим тождеством. Она связывает синус с косинусом. А это значит, чо зная значения синуса, можно найти значения косинуса и наоборот.

 (2)
(2)

 (3)
(3)
В этих равенствах знаки перед корнем определяются по знакам синуса и косинуса.
4.Закрепление
Пример1. Найти  , если
, если  ,
,  .
.
Выясним знак косинуса. Из условия определяем, что угол  в 4 четверти,
в 4 четверти,  Подставим значение
Подставим значение  в формулу (3), получаем:
в формулу (3), получаем:
 Ответ:
Ответ:  .
.
Пример2. Могут ли одновременно выполняться равенства  и
и 
Чтобы одновременно выполнялись эти равенства, необходимо выполнение условия
 . Подставим данные значения в формулу и проверим верно ли равенство: .
. Подставим данные значения в формулу и проверим верно ли равенство: .
 ;
;  1=1, верно.
1=1, верно.
Ответ: данные равенства могут выполняться одновременно
Пример3. Известно, что  , найти
, найти  .
.
Возведём в квадрат левую и правую части равенста:

 ; учтём, что
; учтём, что  ,
,
 ;
;  ;
; 
А какая же зависимость между тангенсом и котангенсом одного угла?
По определению :  ,
,  .
.
Перемножим эти равенства и получим формулу, которая связывает тангенс и котангенс:
 .
.
 , (4)
, (4)
 и
и  , причём угол
, причём угол  и
и 
Из этих формул видно, что тангенс и котангенс являются взаимнообратными числами.
Если , то
, то  . Пример4. Могут ли одновременно выполняться равенства
. Пример4. Могут ли одновременно выполняться равенства  и
и  ? Подставляем данные значения в формулу (4) и получаем верное равенство.
? Подставляем данные значения в формулу (4) и получаем верное равенство.
 .
.
Ответ: данные равенства могут выполняться одновременно.
А есть ли связь между тангенсом и косинусом? Рассмотрим равенство 
и обе части возведём в квадрат: . Используя формулы (2) и (3), получаем:
. Используя формулы (2) и (3), получаем:
 ,
,  , (5) где
, (5) где 
По этой формуле можно находить значение тангенса по заданному значению косинуса и наоборот находить косинус, если известен тангенс.
Пример5 . Известно, что  ;
;  . Найти
. Найти  ,
,  и
и  .
.
Угол  в первой четверти, значит все значения положительны. Найдём их по тригонометрическим формулам.
в первой четверти, значит все значения положительны. Найдём их по тригонометрическим формулам.
 ;
; ;
; .
.
Применяя тригонометрические формулы, можно зная одно из чисел  ,
,  ,
,  и
и  , найти остальные три. Эти формулы являются тождествами.
, найти остальные три. Эти формулы являются тождествами.
Просмотр содержимого документа
«Основные тригонометрические тождества.»
Дата проведения:
Тема урока: Основные тригонометрические тождества.
Тип урока: урок усвоения новых знаний
ЦЕЛИ УРОКА:
1)ОБРАЗОВАТЕЛЬНАЯ: вывод формул зависимости между синусом, косинусом и тангенсом одного и того же угла (числа); обучение применению этих формул для вычисления значений синуса, косинуса, тангенса числа по заданному значению одного из них.
2)РАЗВИВАЮЩАЯ: учить анализировать, сравнивать, строить аналогии, обобщать и систематизировать, доказывать и опровергать, определять и объяснять понятия..
3)ВОСПИТАТЕЛЬНАЯ: воспитание добросовестного отношения к труду и положительного отношения к знаниям.
ДИДАКТИЧЕСКОЕ ОБЕСПЕЧЕНИЕ УРОКА: учебник, тетрадь, плакаты по теме урока, таблицы.
Литература: А.Н.Колмогоров; А.Ш.Алимов
ХОД УРОКА
1. Организационный момент: приветствие, проверка явки учащихся, заполнение журнала.
2. Проверка готовности учащихся к уроку: настрой учащихся на работу, доведение до них плана урока.
3. Новая тема: Рассмотрим точку В(х;у), лежащую на тригонометрической окружности . Она получена поворотом точки А(1;0) вокруг начала координат на угол 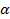 .
.
Синусом угла 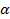 является ордината точки В(х;у). Косинусом угла
является ордината точки В(х;у). Косинусом угла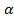 является её абсцисса.
является её абсцисса.
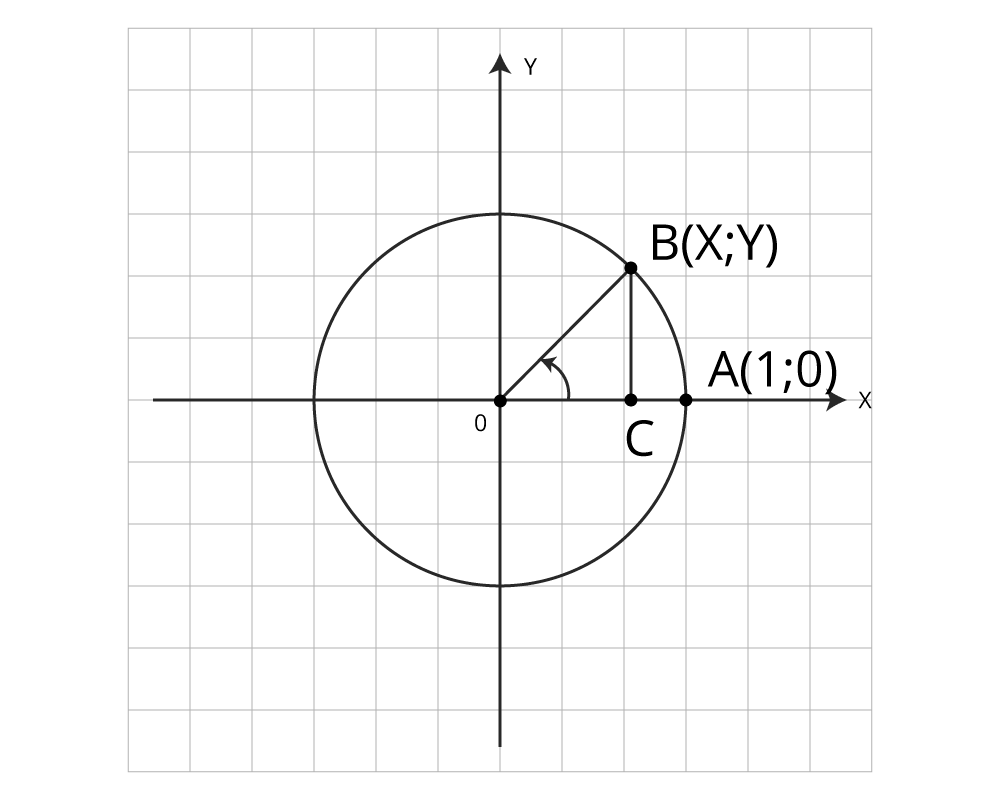
Рисунок 1 – точка В на тригонометрической окружности
Образовался прямоугольный треугольник ОВС. По теореме Пифагора 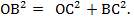
Катет ОС - это абсцисса точки В или 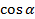 , катет ВС- её ордината, или
, катет ВС- её ордината, или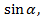 а гипотенуза ОВ - радиус единичной окружности, ОВ=1.Получаем формулу:
а гипотенуза ОВ - радиус единичной окружности, ОВ=1.Получаем формулу:
 (1)
(1)
В тригонометрии её называют основным тригонометрическим тождеством. Она связывает синус с косинусом. А это значит, чо зная значения синуса, можно найти значения косинуса и наоборот.
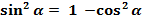
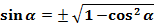 (2)
(2)
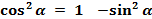
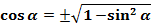 (3)
(3)
В этих равенствах знаки перед корнем определяются по знакам синуса и косинуса.
4.Закрепление
Пример1. Найти 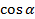 , если
, если 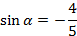 ,
, 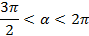 .
.
Выясним знак косинуса. Из условия определяем, что угол 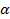 в 4 четверти,
в 4 четверти, 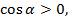 Подставим значение
Подставим значение 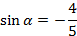 в формулу (3), получаем:
в формулу (3), получаем:
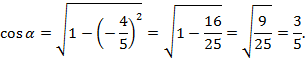 Ответ:
Ответ: 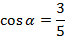 .
.
Пример2. Могут ли одновременно выполняться равенства 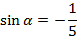 и
и 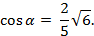
Чтобы одновременно выполнялись эти равенства, необходимо выполнение условия
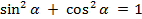 . Подставим данные значения в формулу и проверим верно ли равенство: .
. Подставим данные значения в формулу и проверим верно ли равенство: .
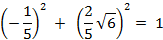 ;
; 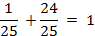 1=1, верно.
1=1, верно.
Ответ: данные равенства могут выполняться одновременно
Пример3. Известно, что 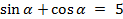 , найти
, найти 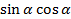 .
.
Возведём в квадрат левую и правую части равенста:
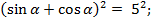
 ; учтём, что
; учтём, что 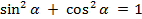 ,
,
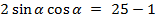 ;
;  ;
; 
А какая же зависимость между тангенсом и котангенсом одного угла?
По определению : 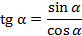 ,
, 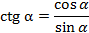 .
.
Перемножим эти равенства и получим формулу, которая связывает тангенс и котангенс:
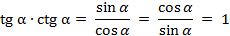 .
.
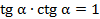 , (4)
, (4)
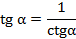 и
и 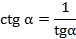 , причём угол
, причём угол 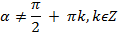 и
и 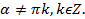
Из этих формул видно, что тангенс и котангенс являются взаимнообратными числами.
Если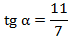 , то
, то 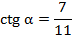 . Пример4. Могут ли одновременно выполняться равенства
. Пример4. Могут ли одновременно выполняться равенства 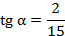 и
и 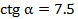 ? Подставляем данные значения в формулу (4) и получаем верное равенство.
? Подставляем данные значения в формулу (4) и получаем верное равенство.
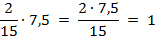 .
.
Ответ: данные равенства могут выполняться одновременно.
А есть ли связь между тангенсом и косинусом? Рассмотрим равенство 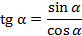
и обе части возведём в квадрат: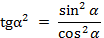 . Используя формулы (2) и (3), получаем:
. Используя формулы (2) и (3), получаем:
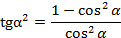 ,
, 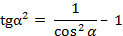 , (5) где
, (5) где 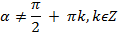
По этой формуле можно находить значение тангенса по заданному значению косинуса и наоборот находить косинус, если известен тангенс.
Пример5 . Известно, что 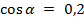 ;
; 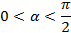 . Найти
. Найти 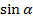 ,
, 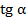 и
и 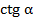 .
.
Угол 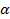 в первой четверти, значит все значения положительны. Найдём их по тригонометрическим формулам.
в первой четверти, значит все значения положительны. Найдём их по тригонометрическим формулам.
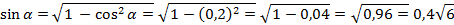 ;
;
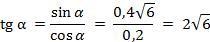 ;
;
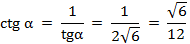 .
.
Применяя тригонометрические формулы, можно зная одно из чисел 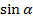 ,
, 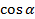 ,
, 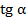 и
и 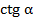 , найти остальные три. Эти формулы являются тождествами.
, найти остальные три. Эти формулы являются тождествами.
Определение: Равенство, верное для всех допустимых значений входящих в него букв (таких, при которых его левая и правая части имеют смысл), называется тождеством, а задачи на доказательство таких равенств называют задачами на доказательство тождеств.
5.Итог урока
Оценивание, Д/З






 .
. является ордината точки В(х;у). Косинусом угла
является ордината точки В(х;у). Косинусом угла является её абсцисса.
является её абсцисса.

 , катет ВС- её ордината, или
, катет ВС- её ордината, или а гипотенуза ОВ - радиус единичной окружности, ОВ=1.Получаем формулу:
а гипотенуза ОВ - радиус единичной окружности, ОВ=1.Получаем формулу: (1)
(1)
 (2)
(2)
 (3)
(3) , если
, если  ,
,  .
. в 4 четверти,
в 4 четверти,  Подставим значение
Подставим значение  в формулу (3), получаем:
в формулу (3), получаем: Ответ:
Ответ:  .
. и
и 
 . Подставим данные значения в формулу и проверим верно ли равенство: .
. Подставим данные значения в формулу и проверим верно ли равенство: . ;
;  1=1, верно.
1=1, верно.  , найти
, найти  .
.
 ; учтём, что
; учтём, что  ,
, ;
;  ;
; 
 ,
,  .
. .
. , (4)
, (4) и
и  , причём угол
, причём угол  и
и 
 , то
, то  . Пример4. Могут ли одновременно выполняться равенства
. Пример4. Могут ли одновременно выполняться равенства  и
и  ? Подставляем данные значения в формулу (4) и получаем верное равенство.
? Подставляем данные значения в формулу (4) и получаем верное равенство. .
.
 . Используя формулы (2) и (3), получаем:
. Используя формулы (2) и (3), получаем: ,
,  , (5) где
, (5) где 
 ;
;  . Найти
. Найти  ,
,  и
и  .
. в первой четверти, значит все значения положительны. Найдём их по тригонометрическим формулам.
в первой четверти, значит все значения положительны. Найдём их по тригонометрическим формулам. ;
; ;
; .
. ,
,  ,
,  и
и  , найти остальные три. Эти формулы являются тождествами.
, найти остальные три. Эти формулы являются тождествами.
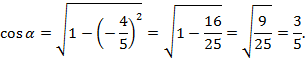 Ответ:
Ответ: 









