§15 Полярная система координат
Кроме знакомой нам прямоугольной системы координат  на плоскости можно рассматривать и другие системы координат. Одной из них является полярная система координат.
на плоскости можно рассматривать и другие системы координат. Одной из них является полярная система координат.
Выберем на плоскости произвольно точку  и назовём её полюсом. Из этой точки
и назовём её полюсом. Из этой точки  проведём какой – нибудь луч
проведём какой – нибудь луч  , считая направление луча положительным. Если на луче
, считая направление луча положительным. Если на луче  выбрать единицу измерения, то этот луч превратится в ось, которую называют полярной осью. Совокупность полюса и полярной оси образует полярную систему координат. Пусть
выбрать единицу измерения, то этот луч превратится в ось, которую называют полярной осью. Совокупность полюса и полярной оси образует полярную систему координат. Пусть  произвольная точка плоскости, на которой задана полярная система координат. Тогда точку
произвольная точка плоскости, на которой задана полярная система координат. Тогда точку  можно единственным образом охарактеризовать с помощью двух параметров: расстояния
можно единственным образом охарактеризовать с помощью двух параметров: расстояния 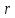 от
от  до полюса
до полюса  , которое называют полярным радиусом точки
, которое называют полярным радиусом точки  , и углом
, и углом  , который образует вектор
, который образует вектор  с полярной осью. Этот угол
с полярной осью. Этот угол  называют полярным углом (см. рисунок 5). При этом пару чисел
называют полярным углом (см. рисунок 5). При этом пару чисел 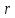 и
и  называют полярными координатами точки
называют полярными координатами точки  , и этот факт обозначают символом
, и этот факт обозначают символом  . Поскольку точка
. Поскольку точка  на плоскости была взята произвольно, то утверждаем, что любую точку плоскости можно определить по её полярным координатам
на плоскости была взята произвольно, то утверждаем, что любую точку плоскости можно определить по её полярным координатам  .
.

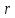





O
1



Рисунок 5.
Теперь рассмотрим связь между декартовыми и полярными координатами произвольно взятой точки на плоскости. Предположим, что на плоскости заданы прямоугольная декартова система координат  и полярная система координат с полюсом
и полярная система координат с полюсом  и полярной осью
и полярной осью  . При этом, расположим полярную систему координат так, чтобы полюс
. При этом, расположим полярную систему координат так, чтобы полюс  совпал с началом
совпал с началом  декартовой системы координат, полярная ось ℓ совпала с положительной полуосью
декартовой системы координат, полярная ось ℓ совпала с положительной полуосью  и единица измерения полярной системы координат совпала с единицей измерения оси
и единица измерения полярной системы координат совпала с единицей измерения оси  .
.
Возьмём произвольно точку  на плоскости и пусть
на плоскости и пусть  её декартовы координаты, а
её декартовы координаты, а  её полярные координаты (см. рис. 6).
её полярные координаты (см. рис. 6).





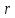



1











O
1

Рисунок 6.
Проведём перпендикуляр  из точки
из точки  к оси
к оси  и рассмотрим треугольник
и рассмотрим треугольник  .
.
Из этого треугольника находим . Получили выражение декартовых
координат  и
и  через полярные координаты
через полярные координаты 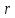 и
и  . Обратим внимание на то, что на рисунке 6 точка
. Обратим внимание на то, что на рисунке 6 точка  взята в первой четверти. Посмотрим, что будет, если точку
взята в первой четверти. Посмотрим, что будет, если точку  взять во второй четверти (см. рисунок 7). Здесь из треугольника
взять во второй четверти (см. рисунок 7). Здесь из треугольника  получаем
получаем








1






1
O






Рисунок 7.
, или . Отсюда находим .
Аналогично проверяется справедливость этих равенств в случаях, когда точка  находится в третьей или четвёртой четвертях.
находится в третьей или четвёртой четвертях.
Теперь выразим полярные координаты 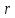 и
и  точки
точки  через декартовы координаты
через декартовы координаты  и
и  . Из того же треугольника
. Из того же треугольника  получаем
получаем  , а для нахождения угла
, а для нахождения угла  нужно учесть знаки
нужно учесть знаки  и
и  и равенство
и равенство  .
.
Найдём, например, полярные координаты точки  . Сначала найдём полярный радиус этой точки:
. Сначала найдём полярный радиус этой точки:  . Для нахождения полярного угла заметим, что точка
. Для нахождения полярного угла заметим, что точка  лежит в третьей четверти. Следовательно, полярный угол
лежит в третьей четверти. Следовательно, полярный угол  точки
точки  удовлетворяет условию
удовлетворяет условию  . Проведём перпендикуляр
. Проведём перпендикуляр  к оси
к оси  и из треугольника
и из треугольника  найдём угол
найдём угол  . Легко видеть, что
. Легко видеть, что  , а значит, . Поэтому полярный угол
, а значит, . Поэтому полярный угол  данной точки
данной точки  равен
равен  .
.
Предположим, что некоторая непрерывная кривая на плоскости задана в полярных координатах, т.е уравнением  . Для построения какой-нибудь точки
. Для построения какой-нибудь точки  данной кривой мы должны провести луч из полюса под углом
данной кривой мы должны провести луч из полюса под углом  к полярной оси и отложить на этом луче отрезок длины
к полярной оси и отложить на этом луче отрезок длины . Придавая
. Придавая  несколько значений и вычисляя
несколько значений и вычисляя 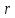 для каждого из них по формуле
для каждого из них по формуле , получим несколько точек кривой. Затем, учитывая непрерывность кривой, плавно соединим полученные точки. Рассмотрим примеры кривых, заданных в полярной системе координат.
, получим несколько точек кривой. Затем, учитывая непрерывность кривой, плавно соединим полученные точки. Рассмотрим примеры кривых, заданных в полярной системе координат.
 , где
, где  некоторое положительное число.
некоторое положительное число.
Из задания кривой легко заметить, что полярный радиус любой точки кривой не зависит от полярного угла  . Значит, какой бы луч из полюса мы не провели, на нём надо отложить отрезок длины
. Значит, какой бы луч из полюса мы не провели, на нём надо отложить отрезок длины  . Другими словами данная кривая представляет собой множество точек, равноудалённых от полюса на расстояние
. Другими словами данная кривая представляет собой множество точек, равноудалённых от полюса на расстояние  . Это есть окружность радиуса
. Это есть окружность радиуса  , центр которой находится в полюсе (см. рисунок 8).
, центр которой находится в полюсе (см. рисунок 8).






O
Рисунок 8.
2)  , где
, где  некоторое положительное число.
некоторое положительное число.
Составим таблицу некоторых значений  , для которых мы знаем значение косинуса. Заметим также, что функция
, для которых мы знаем значение косинуса. Заметим также, что функция  является чётной. Поэтому
является чётной. Поэтому  .
.
Обратим внимание на то, что при некоторых значениях  мы получили отрицательные значения для
мы получили отрицательные значения для 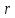 . Это означает, что противоположные полученным (т.е.положительные) значения
. Это означает, что противоположные полученным (т.е.положительные) значения 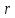 нужно откладывать не на самих лучах, а на лучах, им противоположных. Например, при
нужно откладывать не на самих лучах, а на лучах, им противоположных. Например, при  имеем
имеем  . Лучом, противоположным для
. Лучом, противоположным для  является луч
является луч  . Поэтому отрезок длины
. Поэтому отрезок длины  нужно отложить на луче
нужно отложить на луче  . Но как видим из таблицы, такое значение
. Но как видим из таблицы, такое значение  уже в ней имеется. Таким образом, значение
уже в ней имеется. Таким образом, значение  не даёт новой точки данной кривой. Мы попадаем в уже имеющуюся точку. То же самое получится при
не даёт новой точки данной кривой. Мы попадаем в уже имеющуюся точку. То же самое получится при  , а также при
, а также при  и
и  . Значит, из построенной таблицы мы получим всего 6 точек кривой (при
. Значит, из построенной таблицы мы получим всего 6 точек кривой (при  ,
,  ,
,  ,
,  ). Соединив плавно эти точки, получим данную кривую (см. рисунок 9).
). Соединив плавно эти точки, получим данную кривую (см. рисунок 9).











Рисунок 9.
Если построение было выполнено аккуратно, то можно заметить, что полученная кривая напоминает окружность. Для подтверждения догадки найдём уравнение данной кривой в декартовых координатах. Получим.
.
Это знакомое нам уравнение окружности с центром в точке  радиуса
радиуса  .
.
3)  , где
, где  некоторое положительное число.
некоторое положительное число.
Составляем таблицу
Эта кривая называется кардиоидой. Для её построения выберем какое-нибудь конкретное значение  , например,
, например,  . Тогда, имея 7 точек и плавно их соединив, получаем искомую кривую (см. рисунок 10).
. Тогда, имея 7 точек и плавно их соединив, получаем искомую кривую (см. рисунок 10).

ℓ
Рисунок 10
§16 Вычисление площадей плоских фигур в полярных координатах
Не любую фигуру на плоскости удобно разбивать на криволинейные трапеции, чтобы вычислить площадь этой фигуры. Пример такой фигуры изображён на рисунке 11. Эта фигура ограничена двумя лучами, выходящими из одной точки, и некоторой непрерывной кривой  , пересекающей оба луча.
, пересекающей оба луча.





Рисунок 11.
Такую фигуру называют криволинейным сектором. Рассмотрим задачу о нахождении площади криволинейного сектора. Расположим этот сектор так, чтобы его вершина находилась в полюсе полярной системы координат, а лучи, ограничивающие сектор, образовывали с полярной осью углы  и
и  . Положим для определённости, что
. Положим для определённости, что  , а кривая
, а кривая  задана полярным уравнением
задана полярным уравнением  , где функция
, где функция  непрерывна на
непрерывна на  (см. рисунок 12). Разобьём отрезок
(см. рисунок 12). Разобьём отрезок  на части точками
на части точками  . В результате данный криволинейный сектор разобьётся на
. В результате данный криволинейный сектор разобьётся на  маленьких криволинейных секторов (см. рисунок 13). Найдём площадь одного из таких маленьких криволинейных секторов, ограниченного лучами
маленьких криволинейных секторов (см. рисунок 13). Найдём площадь одного из таких маленьких криволинейных секторов, ограниченного лучами  и
и  , где
, где  одно из чисел
одно из чисел  .
.















ℓ












ℓ

Рисунок 12 Рисунок 13
Если разность  достаточна мала, то в силу непрерывности функции
достаточна мала, то в силу непрерывности функции  можно считать, что значения функции
можно считать, что значения функции  на отрезке
на отрезке  мало отличаются друг от друга. Выберем произвольно точку
мало отличаются друг от друга. Выберем произвольно точку  и заменим маленький криволинейный сектор круговым сектором с радиусом
и заменим маленький криволинейный сектор круговым сектором с радиусом  . Тогда его площадь будет равна . Проделав такую операцию со всеми маленькими криволинейными секторами, получим приближённое значение площади данного криволинейного сектора . Для получения точного значения площади криволинейного сектора перейдём к пределу в полученном равенстве при условии, что все
. Тогда его площадь будет равна . Проделав такую операцию со всеми маленькими криволинейными секторами, получим приближённое значение площади данного криволинейного сектора . Для получения точного значения площади криволинейного сектора перейдём к пределу в полученном равенстве при условии, что все  (
( стремятся к нулю Как и при решении задачи о площади криволинейной трапеции обозначим через 𝜆 наибольшую из разностей
стремятся к нулю Как и при решении задачи о площади криволинейной трапеции обозначим через 𝜆 наибольшую из разностей  . Тогда условие
. Тогда условие  обеспечит стремление к нулю всех
обеспечит стремление к нулю всех  и мы получим
и мы получим
 =.
=.
Покажем, как можно найти площадь круга радиуса  , используя полученную формулу. Поместим центр круга радиуса
, используя полученную формулу. Поместим центр круга радиуса  в полюс полярной системы координат на плоскости. Тогда круг можно рассматривать как криволинейный сектор, ограниченный лучами
в полюс полярной системы координат на плоскости. Тогда круг можно рассматривать как криволинейный сектор, ограниченный лучами  ,
,  и непрерывной кривой
и непрерывной кривой  – окружностью, уравнение которой имеет вид
– окружностью, уравнение которой имеет вид  (см. пример 1 из § 15). Значит, применяя полученную формулу, будем иметь
(см. пример 1 из § 15). Значит, применяя полученную формулу, будем иметь
.
Знание формулы для площади криволинейного сектора позволяет при вычислении площадей плоских фигур разбивать их не только на криволинейные трапеции, но и на криволинейные секторы.
В качестве второго примера применения формулы для площади криволинейного сектора найдём площадь фигуры, ограниченной кардиоидой  , где
, где  некоторое положительное число.
некоторое положительное число.
В § 15 эта кривая была построена (см. пример 3). Легко видеть, что кардиоида симметрична относительно полярной оси. Поэтому фигура, ограниченная кардиоидой, лучами  и
и  разбивается на две симметричные фигуры, которые имеют одинаковую площадь. Значит, площадь искомой фигуры может быть найдена как удвоенная площадь той части фигуры, которая ограничена самой кардиоидой и лучами
разбивается на две симметричные фигуры, которые имеют одинаковую площадь. Значит, площадь искомой фигуры может быть найдена как удвоенная площадь той части фигуры, которая ограничена самой кардиоидой и лучами  и
и  . Поэтому имеем
. Поэтому имеем
.
§17. Вычисление объёмов тел.
Рассмотрим в трехмерном пространстве тело  , которое лежит между плоскостями
, которое лежит между плоскостями  и
и  . Требуется вычислить объем этого тела
. Требуется вычислить объем этого тела  . Воспользуемся идеей решения задачи о площади криволинейной трапеции. Разобьем отрезок
. Воспользуемся идеей решения задачи о площади криволинейной трапеции. Разобьем отрезок  произвольным образом на части точками
произвольным образом на части точками  такими, что
такими, что  . Через каждую точку деления
. Через каждую точку деления 
 проведем плоскость, перпендикулярную оси
проведем плоскость, перпендикулярную оси  . В результате данное тело разобьется на
. В результате данное тело разобьется на  более мелких тел. Вычислим объем одного из таких «маленьких» тел, заключенного между плоскостями
более мелких тел. Вычислим объем одного из таких «маленьких» тел, заключенного между плоскостями  и
и  , где
, где  одно из чисел
одно из чисел  . Если разность
. Если разность  будет достаточно малой, то фигуры, полученные в сечении тела
будет достаточно малой, то фигуры, полученные в сечении тела  плоскостями
плоскостями  и
и  , будут незначительно отличаться друг от друга. Геометрически это значит, что рассматриваемое нами маленькое тело будет почти цилиндром, объем которого мы можем найти. Длина высоты этого цилиндра равна
, будут незначительно отличаться друг от друга. Геометрически это значит, что рассматриваемое нами маленькое тело будет почти цилиндром, объем которого мы можем найти. Длина высоты этого цилиндра равна  , а качестве основания можно взять фигуру, полученную в результате сечения тела плоскостью, перпендикулярной оси
, а качестве основания можно взять фигуру, полученную в результате сечения тела плоскостью, перпендикулярной оси  и проходящей через произвольно выбранную точку
и проходящей через произвольно выбранную точку  на оси
на оси  . Таким образом, объем маленького тела, заключенного между плоскостями
. Таким образом, объем маленького тела, заключенного между плоскостями  и
и  , приближенно будет равен
, приближенно будет равен  , где
, где  площадь сечения тела
площадь сечения тела  плоскостью, перпендикулярной оси
плоскостью, перпендикулярной оси  и проходящей через точку
и проходящей через точку  . Если описанную процедуру проделать со всеми маленькими телами, то получим приближенное значение объема тела
. Если описанную процедуру проделать со всеми маленькими телами, то получим приближенное значение объема тела  : . Точное значение объема получим в результате предельного перехода при
: . Точное значение объема получим в результате предельного перехода при  , где
, где 
 . Итак,
. Итак,
,
где  площадь сечения тела плоскостью, перпендикулярной оси
площадь сечения тела плоскостью, перпендикулярной оси  и проходящей через точку
и проходящей через точку  .
.
Вычислим, например, объем пирамиды с площадью основания  и высотой
и высотой  . Расположим пирамиду так, чтобы ее вершина совпала с началом прямоугольной декартовой системы координат в пространстве, а высота пирамиды лежала на положительной полуоси оси
. Расположим пирамиду так, чтобы ее вершина совпала с началом прямоугольной декартовой системы координат в пространстве, а высота пирамиды лежала на положительной полуоси оси  (см. рисунок 14).
(см. рисунок 14).
Рисунок 14.
Выберем произвольно точку  . Обозначим через
. Обозначим через  площадь сечения пирамиды плоскостью, перпендикулярной оси
площадь сечения пирамиды плоскостью, перпендикулярной оси  и проходящей через точку
и проходящей через точку  . Выразим
. Выразим  через
через  , пользуясь свойством сечений пирамиды плоскостями, параллельными основанию: в пирамиде площади сечений плоскостями, параллельными основанию, относятся как квадраты расстояний этих сечений до вершины. Получаем
, пользуясь свойством сечений пирамиды плоскостями, параллельными основанию: в пирамиде площади сечений плоскостями, параллельными основанию, относятся как квадраты расстояний этих сечений до вершины. Получаем  . Отсюда
. Отсюда  . Следовательно,
. Следовательно,
.
Особенно просто вычислять объемы тел, которые получаются в результате вращения криволинейной трапеции, ограниченной прямыми  ,
,  ,
,  и непрерывной кривой
и непрерывной кривой  , вокруг оси
, вокруг оси  . Такие тела называют телами вращения. Упрощение состоит в том, что в сечении тел вращения вокруг оси
. Такие тела называют телами вращения. Упрощение состоит в том, что в сечении тел вращения вокруг оси  плоскостью, перпендикулярной оси
плоскостью, перпендикулярной оси  и проходящей через точку
и проходящей через точку  , получается круг радиуса
, получается круг радиуса  . Поэтому
. Поэтому  , а, значит, объем тела вращения вычисляется по формуле
, а, значит, объем тела вращения вычисляется по формуле
.
Легко сообразить, что ось  не имеет преимущества по сравнению с другими осями координат. Например, для получения тела вращения вокруг оси
не имеет преимущества по сравнению с другими осями координат. Например, для получения тела вращения вокруг оси  следует вокруг оси
следует вокруг оси  вращать криволинейную трапецию, ограниченную прямыми
вращать криволинейную трапецию, ограниченную прямыми  ,
,  ,
,  и непрерывной кривой
и непрерывной кривой  . Тогда объем тела вращения будем вычислять по формуле
. Тогда объем тела вращения будем вычислять по формуле
.
Как пример применения формулы для вычисления объёма тела вращения найдём объем шара радиуса  . Для этого рассмотрим на плоскости
. Для этого рассмотрим на плоскости  криволинейную трапецию, ограниченную осью
криволинейную трапецию, ограниченную осью  и дугой окружности радиуса
и дугой окружности радиуса  с центром в начале координат, лежащей в первой и второй четвертях (см. рисунок 15).
с центром в начале координат, лежащей в первой и второй четвертях (см. рисунок 15).
Вращая такую криволинейную трапецию вокруг оси  , получим шар радиуса
, получим шар радиуса  . Уравнение рассматриваемой дуги окружности имеет вид
. Уравнение рассматриваемой дуги окружности имеет вид  , где
, где  . Значит, объем шара находим по формуле
. Значит, объем шара находим по формуле
Рисунок 15.
§18. Вычисление длины кривой.
Рассмотрим плоскую кривую без самопересечений, заданную параметрически
, где функции  и ψ непрерывны на некотором отрезке
и ψ непрерывны на некотором отрезке  .
.
Предположим, что на кривой выбрано направление, соответствующее возрастанию параметра  . Тогда значению
. Тогда значению  будет соответствовать начальная точка кривой (обозначим ее
будет соответствовать начальная точка кривой (обозначим ее  ), а значению
), а значению  будет соответствовать конечная точка (обозначим ее
будет соответствовать конечная точка (обозначим ее  ).
).
Разобьем отрезок  . на части точками
. на части точками  так, чтобы
так, чтобы  . Каждому значению
. Каждому значению 
 на кривой будет соответствовать точка . Ясно что,
на кривой будет соответствовать точка . Ясно что,  , а
, а  . Соединим последовательно точки
. Соединим последовательно точки  отрезками. В результате получим ломаную, вписанную в кривую
отрезками. В результате получим ломаную, вписанную в кривую  . Отрезок
. Отрезок  назовем
назовем  ым звеном ломаной. По формуле расстояния между двумя точками найдём длину
ым звеном ломаной. По формуле расстояния между двумя точками найдём длину  го звена ломаной:
го звена ломаной:
.
Зная длину каждого звена ломаной, можно найти длину всей ломаной  .
.
Очевидно, что, неограниченно уменьшая разности  ,
,  , мы будем приближать длину ломаной
, мы будем приближать длину ломаной  к длине кривой. Поэтому, обозначив
к длине кривой. Поэтому, обозначив  , назовем
, назовем  длиной кривой
длиной кривой  .
.
Для вычисления длины кривой  потребуем дополнительно, чтобы функции
потребуем дополнительно, чтобы функции  и ψ имели непрерывные производные на
и ψ имели непрерывные производные на  . Тогда функции
. Тогда функции  и ψ будут удовлетворять условиям теоремы Лагранжа на каждом из отрезков
и ψ будут удовлетворять условиям теоремы Лагранжа на каждом из отрезков  . Следовательно,
. Следовательно,
и
.
Поэтому длину ломаной, вписанной в кривую  , можно записать в виде
, можно записать в виде

 .
.
Сравним эту сумму с интегральной суммой 
 для функции на
для функции на  . Рассмотрим разность
. Рассмотрим разность  и сделаем оценку модуля этой разности. Получим.
и сделаем оценку модуля этой разности. Получим.




 .
.
Теперь заметим, что , а .
Поэтому . Таким образом, получаем оценку

По условию функция  непрерывна на
непрерывна на  , а значит и равномерно непрерывна на
, а значит и равномерно непрерывна на  (по теореме Кантора). Следовательно, выбрав произвольно
(по теореме Кантора). Следовательно, выбрав произвольно  , для числа
, для числа  найдем
найдем  такое, что
такое, что
.
Таким образом, если разбить отрезок  на части длиной меньше, чем
на части длиной меньше, чем  , то при всех
, то при всех  будет выполняться условие
будет выполняться условие  . Поэтому из условия
. Поэтому из условия  будем иметь
будем иметь
.
Это значит, что 
 , где
, где 
 , или
, или  .
.
Учитывая, что  , а
, а  представляет собой длину кривой
представляет собой длину кривой  Отсюда получаем формулу для вычисления длины кривой, заданной параметрически , где функции
Отсюда получаем формулу для вычисления длины кривой, заданной параметрически , где функции  и ψ непрерывны и имеют непрерывные производные на
и ψ непрерывны и имеют непрерывные производные на  :
:
.
Если кривая  задана на отрезке
задана на отрезке  уравнением
уравнением  , где функция
, где функция  имеет непрерывную производную на
имеет непрерывную производную на  , то, записывая уравнение кривой в параметрическом виде
, то, записывая уравнение кривой в параметрическом виде  , получаем формулу
, получаем формулу
.
В заключение параграфа рассмотрим специфический случай параметрического задания кривой, когда в качестве параметра используется длина переменной дуги.
Пусть имеем кривую  , заданную параметрически , где функции
, заданную параметрически , где функции  и ψ непрерывны и имеют непрерывные производные на
и ψ непрерывны и имеют непрерывные производные на  . Тогда каждому значению
. Тогда каждому значению  будет соответствовать определенная точка
будет соответствовать определенная точка  на кривой. При этом будем считать, что
на кривой. При этом будем считать, что  , если
, если  и
и  , если
, если  . Заметив, что точка
. Заметив, что точка  единственным образом определяет дугу
единственным образом определяет дугу  кривой
кривой  , можно каждому значению
, можно каждому значению  поставить в соответствие длину дуги
поставить в соответствие длину дуги  , которая будет равна . Другими словами, получим функцию , значениями которой являются длины различных дуг кривой
, которая будет равна . Другими словами, получим функцию , значениями которой являются длины различных дуг кривой  . При этом значению
. При этом значению  будет соответствовать длина
будет соответствовать длина  всей кривой
всей кривой  . Эта функция
. Эта функция  дифференцируема на
дифференцируема на  и по свойству интеграла с переменным верхним пределом .
и по свойству интеграла с переменным верхним пределом .
Если при некотором значении  выполняется условие
выполняется условие  , то точка кривой
, то точка кривой  , соответствующая этому значению
, соответствующая этому значению  , называется особой точкой. Легко видеть, что условие
, называется особой точкой. Легко видеть, что условие  равносильно условию . Будем считать, что на кривой
равносильно условию . Будем считать, что на кривой  особых точек нет. Тогда . Это значит, что функция является монотонно возрастающей на
особых точек нет. Тогда . Это значит, что функция является монотонно возрастающей на  , а, следовательно, имеет обратную функцию
, а, следовательно, имеет обратную функцию  , определенную на
, определенную на  . Таким образом, можно получить новые параметрические уравнения данной кривой , где
. Таким образом, можно получить новые параметрические уравнения данной кривой , где  , в которых параметром служит длина
, в которых параметром служит длина  переменной дуги. Во некоторых вопросах использование параметра
переменной дуги. Во некоторых вопросах использование параметра  вместо произвольного параметра
вместо произвольного параметра  является более удобным.
является более удобным.
§19. Вычисление площадей поверхностей вращения.
Пусть на плоскости имеем кривую  и прямую
и прямую  , не пересекающую
, не пересекающую  . Поверхность, полученную в результате вращения кривой
. Поверхность, полученную в результате вращения кривой  вокруг прямой
вокруг прямой  , называют поверхностью вращения. Предположим, что в кривую
, называют поверхностью вращения. Предположим, что в кривую  вписана ломаная
вписана ломаная  . Легко видеть, что каждое звено ломаной при вращении кривой
. Легко видеть, что каждое звено ломаной при вращении кривой  вокруг прямой
вокруг прямой  опишет либо круговое кольцо (если звено ломаной перпендикулярно
опишет либо круговое кольцо (если звено ломаной перпендикулярно  ), либо боковую поверхность цилиндра (если звено ломаной параллельно
), либо боковую поверхность цилиндра (если звено ломаной параллельно  ), либо боковую поверхность конуса (если один из концов звена ломаной лежит на
), либо боковую поверхность конуса (если один из концов звена ломаной лежит на  ), либо боковую поверхность усеченного конуса (в остальных случаях). Следовательно, при вращении кривой
), либо боковую поверхность усеченного конуса (в остальных случаях). Следовательно, при вращении кривой  ломаная
ломаная  опишет некоторую поверхность, состоящую из круговых колец, боковых поверхностей цилиндра, конуса или усеченного конуса. Обозначим через
опишет некоторую поверхность, состоящую из круговых колец, боковых поверхностей цилиндра, конуса или усеченного конуса. Обозначим через  площадь этой поверхности, и пусть
площадь этой поверхности, и пусть 
 . Тогда площадью поверхности, полученной в результате вращения кривой
. Тогда площадью поверхности, полученной в результате вращения кривой  вокруг прямой
вокруг прямой  , назовем
, назовем  .
.
Перейдем к вычислению площади поверхности вращения. Предположим, что кривая  задана параметрически, а в качестве параметра используется длина переменной дуги
задана параметрически, а в качестве параметра используется длина переменной дуги  , т.е. кривая
, т.е. кривая  задана уравнениями , где функции
задана уравнениями , где функции  и
и  непрерывны и имеют непрерывные производные на
непрерывны и имеют непрерывные производные на  . Будем считать, что вращение осуществляется вокруг оси
. Будем считать, что вращение осуществляется вокруг оси  прямоугольной декартовой системы координат
прямоугольной декартовой системы координат  .
.
Разобьем отрезок  на части точками
на части точками  так, что
так, что  . Для каждого значения
. Для каждого значения 
 получим на кривой точку
получим на кривой точку  . Соединив последовательно точки
. Соединив последовательно точки  , получим ломаную
, получим ломаную  , вписанную в кривую
, вписанную в кривую  , где
, где  ,
,  . Рассмотрим площадь поверхности, образованной вращением отрезка
. Рассмотрим площадь поверхности, образованной вращением отрезка  (
( го звена ломаной). Как уже было отмечено, при этом может получиться круговое кольцо или боковая поверхность цилиндра, конуса или усеченного конуса. Рассматривая круговое кольцо, цилиндр и конус как частные случаи усеченного конуса, найдем площадь поверхности, образованной вращением отрезка
го звена ломаной). Как уже было отмечено, при этом может получиться круговое кольцо или боковая поверхность цилиндра, конуса или усеченного конуса. Рассматривая круговое кольцо, цилиндр и конус как частные случаи усеченного конуса, найдем площадь поверхности, образованной вращением отрезка  вокруг оси
вокруг оси  , по формуле . После суммирования этих равенств по
, по формуле . После суммирования этих равенств по  получим
получим
Сравним эту сумму  с суммой , где
с суммой , где  .
.
Теперь заметим, что длина кривой  не меньше длины хорды
не меньше длины хорды  , т.е.
, т.е.  при всех
при всех  . Просуммировав эти неравенства по
. Просуммировав эти неравенства по  , получим
, получим

 .
.
Следовательно, для разности  имеем следующую оценку
имеем следующую оценку
.
По условию функция 𝛹 непрерывна на  . Поэтому по второй теореме Вейерштрасса среди ее значений есть наибольшее. Обозначим его через
. Поэтому по второй теореме Вейерштрасса среди ее значений есть наибольшее. Обозначим его через  . Тогда имеем и . Таким образом, приходим к неравенству
. Тогда имеем и . Таким образом, приходим к неравенству

 .
.
Перейдем в этом неравенстве к пределу при  . Получим
. Получим


 .
.
Так как  , предел правой части последнего неравенства равен нулю. Значит по теореме о сжатой функции
, предел правой части последнего неравенства равен нулю. Значит по теореме о сжатой функции  , или
, или  .
.
Обозначив  и заметив, что условия
и заметив, что условия  и
и  равносильны, будем иметь
равносильны, будем иметь 
Таким образом, для вычисления площади поверхности вращения  получили формулу
получили формулу
.
Теперь найдём формулу для вычисления площади поверхности вращения для случая, когда кривая  задана параметрически, но в качестве параметра используется не длина переменной дуги. Пусть кривая
задана параметрически, но в качестве параметра используется не длина переменной дуги. Пусть кривая  задана в виде , где
задана в виде , где  , а функции
, а функции  и 𝛹 имеют непрерывные производные на
и 𝛹 имеют непрерывные производные на  . Сделаем замену переменной . Функция
. Сделаем замену переменной . Функция  , определённая на отрезке
, определённая на отрезке  , имеет непрерывную производную ;
, имеет непрерывную производную ;  ,
,  . Поэтому, по теореме 5.7, получаем
. Поэтому, по теореме 5.7, получаем
.
Если же кривая  задана уравнением
задана уравнением  , где
, где  и функция
и функция  имеет непрерывную производную, то .
имеет непрерывную производную, то .
§20. Понятие о несобственных интегралах.
Рассматривая определенный интеграл  , мы считали промежуток интегрирования конечным, а функцию
, мы считали промежуток интегрирования конечным, а функцию  ограниченной на нем. Понятие определенного интеграла можно обобщить в двух направлениях: на случай бесконечного промежутка интегрирования и на случай неограниченной на
ограниченной на нем. Понятие определенного интеграла можно обобщить в двух направлениях: на случай бесконечного промежутка интегрирования и на случай неограниченной на  функции
функции  .
.
Пусть функция  определена на промежутке
определена на промежутке  и интегрируема на любом конечном промежутке
и интегрируема на любом конечном промежутке  . Несобственным интегралом первого рода называют
. Несобственным интегралом первого рода называют 
 и обозначают символом
и обозначают символом  . Если указанный предел конечен, то несобственный интеграл
. Если указанный предел конечен, то несобственный интеграл  называют сходящимся, а функцию
называют сходящимся, а функцию  интегрируемой на
интегрируемой на  . Если же
. Если же 
 не существует или бесконечен, то
не существует или бесконечен, то  называют расходящимся.
называют расходящимся.
Исследуем, например, на сходимость  . Функция
. Функция  интегрируема на любом конечном промежутке
интегрируема на любом конечном промежутке  , причем . Следовательно, . Это значит, что данный интеграл сходится.
, причем . Следовательно, . Это значит, что данный интеграл сходится.
Аналогично можно определить  , а именно, .
, а именно, .
Введем теперь понятие несобственного интеграла первого рода от функции  на интервале
на интервале  . Выберем произвольно число
. Выберем произвольно число  и положим
и положим

Если каждый из интегралов в правой части равенства  сходится, то интеграл
сходится, то интеграл  называют сходящимся. Если же хотя бы один из интегралов в правой части равенства
называют сходящимся. Если же хотя бы один из интегралов в правой части равенства  расходится, то
расходится, то  называют расходящимся.
называют расходящимся.
Допустим теперь, что функция  определена на
определена на  и не ограничена в точке
и не ограничена в точке  . Зададим произвольно
. Зададим произвольно  так, чтобы
так, чтобы  . Если функция
. Если функция  интегрируема на отрезке
интегрируема на отрезке  , то можно определить
, то можно определить  как
как 
 . В этом случае
. В этом случае  называют несобственным интегралом второго рода.
называют несобственным интегралом второго рода.
Он будет сходящимся, если 
 существует и конечен и расходящимся в противном случае.
существует и конечен и расходящимся в противном случае.
Аналогично если функция  определена на
определена на  , не ограничена в точке
, не ограничена в точке  и интегрируема на
и интегрируема на  (где
(где  ), то
), то  определяют как
определяют как 
 . Если функция
. Если функция  не ограничена во внутренней точке
не ограничена во внутренней точке  , но определена во всех остальных точках отрезка, то для определения интеграла
, но определена во всех остальных точках отрезка, то для определения интеграла  отрезок
отрезок  разбивают на два промежутка
разбивают на два промежутка  и
и  и определяют
и определяют  как .
как .
В случае, когда на отрезке  функция
функция  имеет несколько точек неограниченности, его разбивают на несколько промежутков так, чтобы каждый промежуток содержал лишь одну точку неограниченности и определяют
имеет несколько точек неограниченности, его разбивают на несколько промежутков так, чтобы каждый промежуток содержал лишь одну точку неограниченности и определяют  как сумму интегралов на каждом из промежутков.
как сумму интегралов на каждом из промежутков.
Можно показать, что для несобственных интегралов справедливы все свойства и методы интегрирования определенных интегралов.
Рассмотрим пример. Исследуем на сходимость  . Легко видеть, что подинтегральная функция
. Легко видеть, что подинтегральная функция  определена и непрерывна на
определена и непрерывна на  , а в точке
, а в точке  неограничена. Следовательно, данный интеграл является несобственным второго рода. По определению
неограничена. Следовательно, данный интеграл является несобственным второго рода. По определению 

 . Вычислим
. Вычислим  методом замены переменной. Положим
методом замены переменной. Положим  . Найдем новые пределы интегрирования: нижний будет равен
. Найдем новые пределы интегрирования: нижний будет равен  , а верхний
, а верхний  . Таким образом,
. Таким образом,
.
Значит, 

 , т.е
, т.е  сходится.
сходится.
§21. Приближенное вычисление определенных интегралов.
Предположим, что функция  непрерывна, но не интегрируема в конечном виде на
непрерывна, но не интегрируема в конечном виде на  . В таких случаях
. В таких случаях  вычисляют приближенно. Идея вычисления состоит в следующем. Выбираем некоторое разбиение
вычисляют приближенно. Идея вычисления состоит в следующем. Выбираем некоторое разбиение  с отмеченными точками отрезка
с отмеченными точками отрезка  ., составляем интегральную сумму
., составляем интегральную сумму  и заменяем точное равенство на приближенное . Для упрощения вычислений отрезок
и заменяем точное равенство на приближенное . Для упрощения вычислений отрезок  обычно разбивают на равные части, а точки
обычно разбивают на равные части, а точки  выбирают по одному и тому же правилу для всех
выбирают по одному и тому же правилу для всех 
 . Например, в качестве
. Например, в качестве  можно выбрать один из концов отрезка
можно выбрать один из концов отрезка  , середину отрезка
, середину отрезка  или еще как-нибудь.
или еще как-нибудь.
Поскольку отрезок  разбивают на равные части, то параметр разбиения . Эту величину
разбивают на равные части, то параметр разбиения . Эту величину  называют шагом разбиения и обычно обозначают через
называют шагом разбиения и обычно обозначают через  .
.
Рассмотрим некоторые формулы приближенного вычисления определенных интегралов.
Пусть, например, в качестве точек  выбраны середины отрезков
выбраны середины отрезков  , т.е.
, т.е.  , или
, или  .
.
Тогда 
 , или
, или 
 .
.
Эту формулу называют формулой прямоугольников.
Если в качестве точек  выбрать такие точки, чтобы , то получим
выбрать такие точки, чтобы , то получим
, или .
Эту формулу называют формулой трапеций.
Ясно, что точность приближенного вычисления определенных интегралов зависит от  Чем больше число точек деления отрезка
Чем больше число точек деления отрезка  (чем меньше шаг
(чем меньше шаг  ), тем точнее результат. Современный уровень развития вычислительной техники позволяет вычислять определенные интегралы практически с любой степенью точности.
), тем точнее результат. Современный уровень развития вычислительной техники позволяет вычислять определенные интегралы практически с любой степенью точности.
118






 на плоскости можно рассматривать и другие системы координат. Одной из них является полярная система координат.
на плоскости можно рассматривать и другие системы координат. Одной из них является полярная система координат. и назовём её полюсом. Из этой точки
и назовём её полюсом. Из этой точки  , считая направление луча положительным. Если на луче
, считая направление луча положительным. Если на луче  произвольная точка плоскости, на которой задана полярная система координат. Тогда точку
произвольная точка плоскости, на которой задана полярная система координат. Тогда точку  можно единственным образом охарактеризовать с помощью двух параметров: расстояния
можно единственным образом охарактеризовать с помощью двух параметров: расстояния 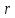 от
от  до полюса
до полюса  , который образует вектор
, который образует вектор  с полярной осью. Этот угол
с полярной осью. Этот угол  . Поскольку точка
. Поскольку точка  .
.












