Понятие Движение

Понятие движения

Если каждой точке плоскости ставится в соответствие какая-то точка этой же плоскости, причем любая точка плоскости оказывается сопоставленной некоторой точке, то говорят, что дано отображение плоскости на себя .

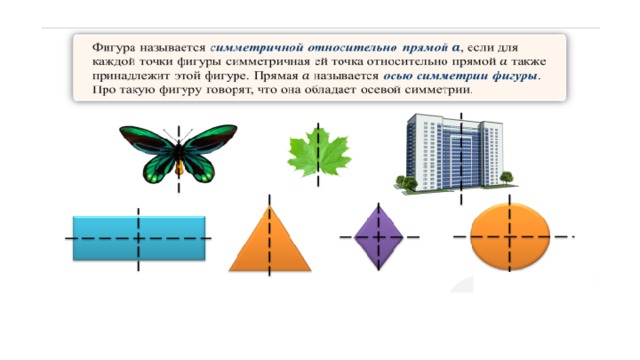
Фигура называется симметричной относительно точки , если для каждой точки фигуры симметричная ей точка относительно точки также принадлежит этой фигуре. Точка называется центром симметрии фигуры .

Симметрия – это идея, с помощью которой человек веками пытался объяснить и создать порядок, красоту и совершенство.

Г. Вейль

Принципы симметрии играют важную роль в физике и математике, химии и биологии, технике и архитектуре, живописи и скульптуре, поэзии и музыке.

Законы природы, управляющие неисчерпаемой в своём многообразии картиной явлений, в свою очередь, также подчиняются принципам симметрии.

Немного истории

• Термин «симметрия» придумал скульптор Пифагор Регийский.

• Древние греки полагали, что Вселенная симметрична просто потому, что она прекрасна.

• Первую научную школу в истории человечества создал Пифагор Самосский.
• «Симметрия – это некая «средняя мера», - считал Аристотель .
• Римский врач Гален (2 в. н. э.) под симметрией понимал покой души и уравновешенность.

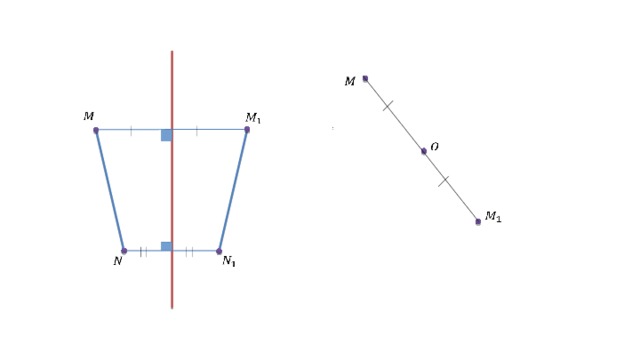
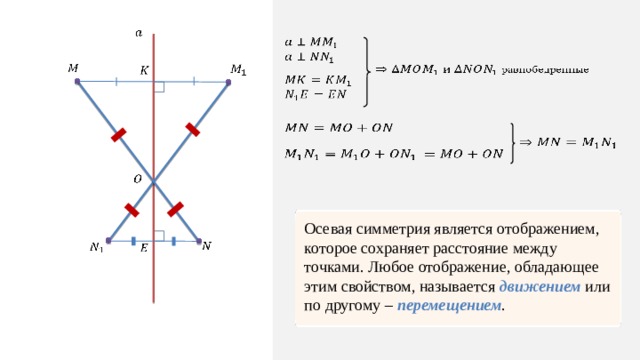
Осевая симметрия является отображением, которое сохраняет расстояние между точками. Любое отображение, обладающее этим свойством, называется движением или по другому – перемещением .

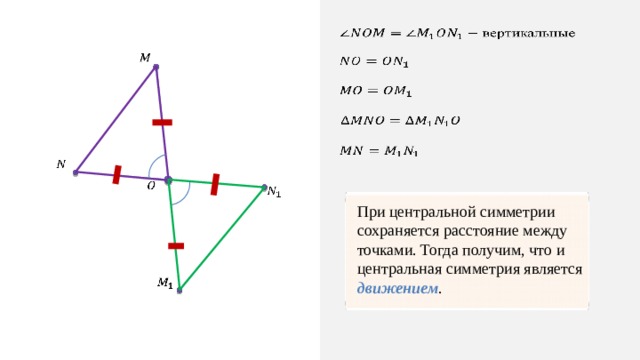
При центральной симметрии сохраняется расстояние между точками. Тогда получим, что и центральная симметрия является движением .

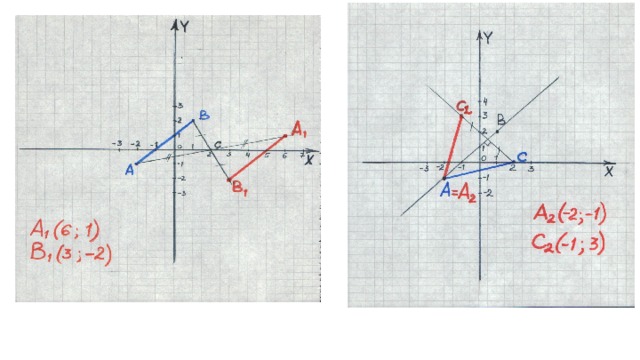
А(-2;-1), В(1;2), С(2;0)

1 . Построить отрезок А 1 В 1 , симметричный отрезку АВ

относительно точки C.

2. Построить отрезок А 2 C 2 , симметричный отрезку АC относительно прямой АB.

Понятие движения

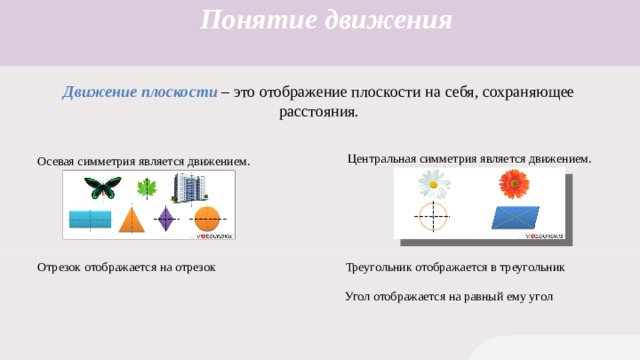
Движение плоскости – это отображение плоскости на себя, сохраняющее расстояния.

Центральная симметрия является движением.

Осевая симметрия является движением.

Отрезок отображается на отрезок

Треугольник отображается в треугольник

Угол отображается на равный ему угол