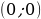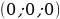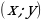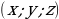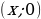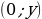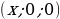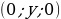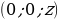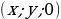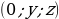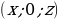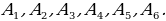ГБПОУ «Починковский сельскохозяйственный техникум»
Согласовано
Зам.директора по УПР
________С.В.Мартынова
методист
________М.В.Шишова
Открытый урок на тему:
«Декартовы координаты в пространстве».
Выполнила:
преподаватель математики
Абросимова Е.А.
с. Починки, 2025 г.
Декартовы координаты в пространстве.
“… потомки будут благодарны мне не только за то, что я сказал, но и за то, что я не сказал и тем самым дал им возможность и удовольствие додуматься до этого самостоятельно”.
Рене Декарт
Цель – научить строить точки в пространстве по заданным координатам и определять координаты точки в пространстве.
Задачи урока:
Образовательные:
рассмотреть понятие системы координат в пространстве;
рассмотреть понятие координаты точки в пространстве;
Развивающие:
способствовать развитию пространственного воображения учащихся;
способствовать выработке навыка решения задач и развития логического мышления учащихся.
Воспитательные: воспитание познавательной активности, чувства ответственности, культуры общения, культуры диалога.
Оборудование: презентация к уроку, чертежные принадлежности, каркасная модель куба.
Тип урока: Урок изучения нового материала.
Технология обучения: Технология программированного обучения (блочное обучение).
Структура урока:
Организационный момент.
Сообщение цели и задач урока.
Введение.
Историческая справка.
Мотивация.
Повторение.
Изучение нового материала.
Актуализация ранее полученных знаний.
Осмысление и осознание изученного.
Закрепление.
Итог урока.
Домашнее задание: Гл. 7, § 1 п. 71-73, № 641, № 647, № 655.
Ход урока:
Слайд 1
Организационный момент.
Сообщение целей урока. Сегодня мы начинаем изучать блок курса геометрии 11 класса «Координаты и векторы в пространстве». Какую тему созвучную с темой нашего урока мы изучали в 8 классе? Какое ключевое слово определяют эти две темы? (Координаты). В чём различие в названиях? Сегодня на уроке мы будем изучать новый материал, проводя аналогию с уже известным.
Мы продолжим изучение декартовой системы координат, и убедимся в том, что координаты в пространстве вводятся также просто, как и координаты на плоскости.
Введение.
Слайд 3,4,5
Историческая справка. В 1637 г. во Франции вышла книга, которая принесла её автору невероятную известность. По обычаям того времени она имела довольно длинное название: «Рассуждение о методе, позволяющем направлять разум и отыскивать истину в науках. Кроме того, Диоптрика, Метеоры и Геометрия, которые являются приложениями этого метода».
Автор книги Рене Декарт (1596 – 1650 г.). Декарт был крупнейшим философом и математиком своего времени. Самым известным трудом Декарта является его “Геометрия”. Декарт ввел систему координат, которой пользуются все и в настоящее время. Он установил соответствие между числами и отрезками прямой и таким образом ввел алгебраический метод в геометрию. Эти открытия Декарта дали огромный толчок развитию как геометрии, так и другим разделам математики и оптики. Появилась возможность изображать зависимость величин графически на координатной плоскости, числа - отрезками и выполнять арифметические действия над отрезками и другими геометрическими величинами, а также различными функциями. Это был совершенно новый метод, отличавшийся красотой, изяществом и простотой. В ней он ввел прямоугольную систему координат, поставил каждой точке в соответствие пару чисел – её координаты. Этот прогрессивный метод позволил решить ряд геометрических задач алгебраическим методом, что оказалось очень удобным.
Первое определение IX книги «Начала» Евклида гласит: «Тело есть то, что имеет длину, ширину и глубину». Тем не менее, есть основание полагать, что в древности нашего понятия о трехмерном пространстве не существовало. У Декарта имелись лишь далекие намеки на возможность распространения метода координат с двумерного пространства (плоскости) на трёхмерное. Потребовалось ещё почти 100 лет, чтобы идея пространственных координат была сформирована, постоянно и широко использовалась.
Мотивация. В своё время Рене Декарт сказал: «… потомки будут благодарны мне не только за то, что я сказал, но и за то, что я не сказал и тем самым дал им возможность и удовольствие додуматься до этого самостоятельно». Я предоставлю вам возможность и удовольствие разобраться с декартовой системой координат самостоятельно.
Слайд 6, 7. Задание на повторение.
На координатной плоскости нарисуйте ломаную, вершины которой имеют координаты:
(0; 0), (-1; 1), (-3; 1), (-2; 3), (-3; 3), (-4; 6), (0; 8), (2; 5), (2; 11), (6; 10), (3; 9), (4; 5), (3; 0),( 2; 0), (1; -7), (3; -8), (0; -8),(0; 0).
Слайд 8, 9. Подведение к теме урока.

Слайд 10-13. Изучение нового материала.
На основе известного материала мы сделаем сравнительную характеристику координатного метода и заполним таблицу.
На слайдах приготовлена таблица. Точно такая же таблица – в тетрадях. Её необходимо заполнить вместе с учениками. При заполнении первой строки в обоих столбиках, определения только проговорить, в таблице – рисунки, на которых в ходе беседы появятся начало координат, единичный отрезок.
|
| на плоскости | в пространстве |
| определение | Прямоугольной системой координат называется совокупность двух перпендикулярных прямых (координатных осей) и точки, в которой эти оси пересекаются (начала координат). 
| Прямоугольной системой координат называется совокупность трёх перпендикулярных прямых (координатных осей) и точки, в которой эти оси пересекаются (начала координат). 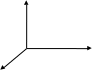
|
| оси | ОУ- ось ординат ОХ- ось абсцисс
| ОХ - ось абсцисс ОУ – ось ординат ОZ - ось аппликат |
| начало координат | 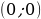
| 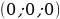
|
| координаты точек | 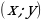
| 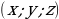
|
| особое расположение точек | на оси OX 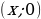 на оси OY 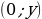 | на оси OX 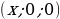 на оси OY 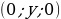 на оси OZ 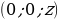 на плоскости XOY 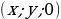 на плоскости YOZ 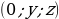 на плоскости XOZ 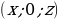 |
Слайд 14
Попробуем сформулировать определение декартовой системы координат в пространстве?
Декартова система координат в пространстве — это упорядоченная система трёх взаимно перпендикулярных осей в пространстве с общим началом отсчёта и одинаковой масштабной единицей.
Назовите оси координат в пространстве? Название, какой оси мы не изучали? (Знакомство с новым словом “аппликата”)
Какие плоскости рассматриваются в пространстве?
Назовите координату начала координат в пространстве?
Какие еще компоненты должна иметь система координат на плоскости и в пространстве? (единичный отрезок)
Как задается координата точки на плоскости и в пространстве?
Вывод:
Расскажите, как вводится, декартова система координат в пространстве и из чего она состоит?
Слайд 15
Переписать схему в тетрадь.
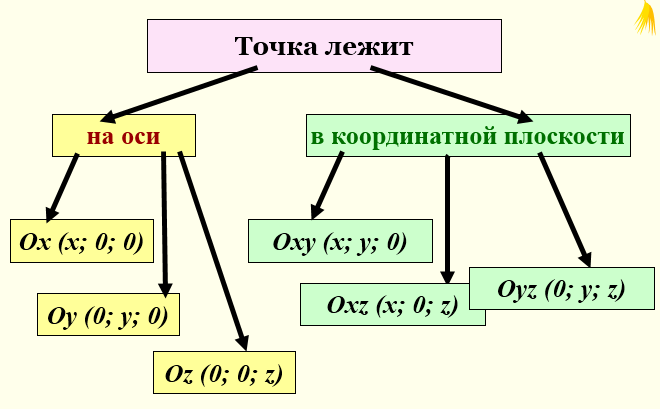
Слайд 16, 17
Всё показываю на макете прямоугольной системы координат – каркасной модели куба.
Задание 1. Построить точку с заданными координатами А (2; -3; 5) – я показываю на доске, группа строит в тетрадях. Найти координаты точек 
Слайд 18
Задание 2. Устно. Даны координаты вершин куба…Найдите координаты остальных вершин куба.
Слайд 19, 20
Закрепление изученного материала:
Задание 3. Устно.
Даны точки: А (2; -1; 0), В (0; 0; -7), С (2; 0; 0), D (-4; -1; 0), Е (0; -3; 0), F (1; 2; 3), Р (0; 5; -7), К (2; 0; -4).
Назовите точки, лежащие
в плоскости Оуz.
в плоскости Охz.
в плоскости Оху.
Слайд 21 - 23
Задание 4 Начертить прямоугольную трехмерную систему координат и отметить в ней точки: А (1; 4; 3); В (0; 5; -3); С (0; 0; 3) и D (4; 0; 4)
Слайд 24, 25
Итоги урока.
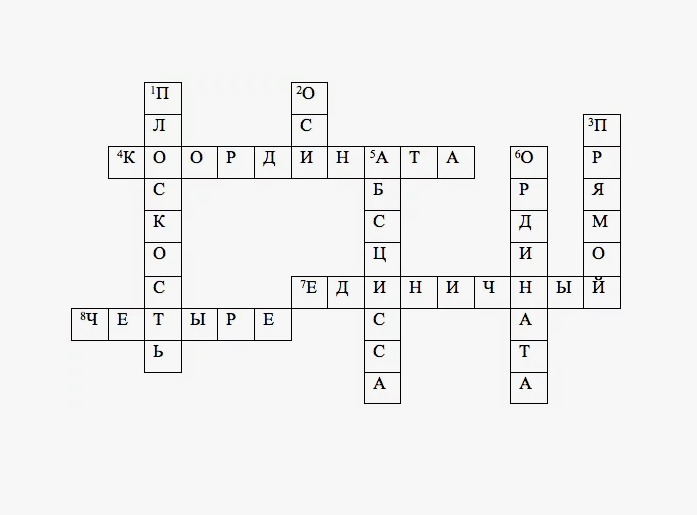
Разгадаем кроссворд:
Две координатные прямые образуют координатную…
Координатные прямые – это координатные…
Какой угол образуется при пересечении координатных прямых?
Как называется пара чисел, определяющих положение точки на плоскости?
Как называется первая координата?
Как называется вторая координата?
Как называется отрезок от 0 до 1?
На сколько частей делится координатная плоскость координатными прямыми?

Итак, что мы сегодня изучили?
Как вводится, декартова система координат? Из чего она состоит?
Как определяются координаты точки в пространстве?
Каковы координаты начала координат?
Оценивание (учитель выставляет оценки за работу на уроке и объявляет их учащимся).
Слайд 26
Домашнее задание: Гл. 7, § 1 п. 71-73, № 641, № 647, № 655.
Слайд 27
Рефлексия.
Слайд 28
Спасибо за урок. До свидания.