Открытый урок по алгебре в 8 классе

Муниципальное казённое общеобразовательное учреждение

средняя общеобразовательная школа № 3

Тема урока

Арифметический квадратный корень

и его свойства

8 «Б» класс

Подготовила:

учитель математики

первой категории

Калинина Е.Ю.

2015-2016 учебный год

Тема урока: Арифметический квадратный корень

и его свойства

Цели:

1.Закрепление навыков использования свойств арифметического квадратного корня для преобразования выражений, содержащих квадратные корни;

2.Отработка внимательности и точности при выполнении заданий;

3.Воспитание интереса к предмету через игровые моменты урока, занимательные задачи, познавательные сюжеты из истории математики;

Задачи:

1.Систематизировать материал по данной теме;

2.Провести диагностику усвоения системы знаний и умений, ее применения для выполнения практических заданий стандартного уровня с переходом на более высокий уровень;

3.Развивать познавательные процессы, память, мышление, внимание, наблюдательность, сообразительность;

4.Выработать критерии оценки своей работы, умение анализировать проделанную работу и адекватно ее оценивать.

Ход урока:

Организационный момент

Представим себе, что сегодня наш класс – научно-исследовательский институт.

А вы, ученики, - сотрудники этого института. А именно, сотрудники различных лабораторий по проблемам математики. Вас всех пригласили принять участие в заседании ученого совета этого НИИ, чтобы обсудить с вами тему «Арифметический квадратный корень и его свойства». В процессе работы в НИИ вы должны: закрепить изученный материал, показать уровень усвоения темы, разобраться в непонятых ранее моментах, проконтролировать и оценить свои знания. У каждого из вас на столе оценочный лист, где вы будете фиксировать свои достижения, и в конце оцените свою работу как сотрудники наших лабораторий.

Оценочный лист.

Оценка «5» 23-26 баллов, Оценка «4» 15-22 баллов, Оценка «3» ниже 15 баллов

Устная работа

1. Вычислить

√0,36; √1600; √0,81; √0,0025

1. Площадь квадрата 0,25 м² . Найти его сторону.

2. Решите уравнение х²=16 х²=0 х²=26 х²= -9

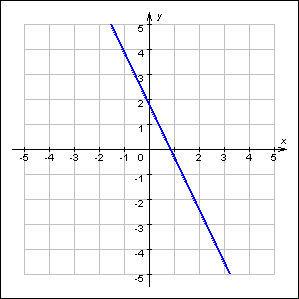
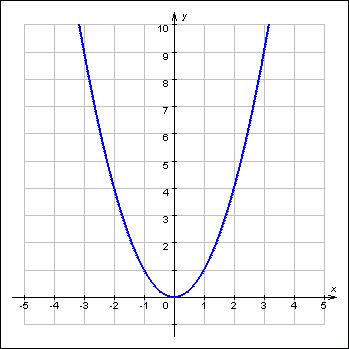
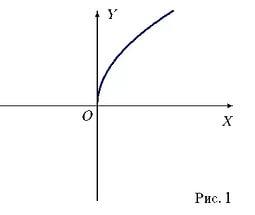
3. Определите вид функции и формулу, задающую эту функцию

Актуализация опорных знаний.

Итак, « лаборатория теоретиков».

Это наша первая лаборатория. В ней вы должны вспомнить теоретический материал по теме, который пригодиться вам в дальнейшей работе в других лабораториях.

• I.Арифметическим квадратным корнем из числа а называется ______________число, квадрат которого равен а.

1.Неположительное 2.Неотрицательное 3.Положительное 4.Отрицательное

II. Квадратным корнем из числа а называют число, _______которого равен а

• 1.куб 2. корень 3. квадрат 4. площадь

• III. Уравнение вида х² = а не имеет корней, если

• 1. а=0 2. а≤ 0 3.а ‹ 0 4.а ≥ 0

IV. На каком из рисунков изображен график функции ?

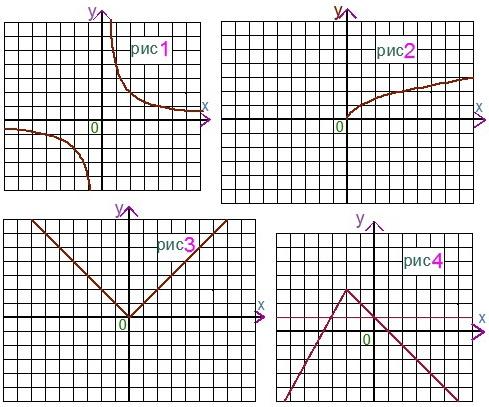
Молодцы! Оцените свою работу в лаборатории теоретиков по 4-ех бальной системе.

Лаборатория теоретиков была пропуском в следующую лабораторию, которая называется «Лаборатория исследований»

Давайте разделимся на группы, каждая группа получает задания. Вам надо исследовать полученные вопросы, а затем представитель от каждой группы выступит и расскажет свою версию решения.

I группа Одна из точек, отмеченных на координатной прямой, соответствует числу 3√2. Какая это точка?

II группа Расположите в порядке убывания числа 4 -√20; -2; √8

III группа Одно из чисел √20; 10√2; 2√10; √30 отмечено на координатной прямой точкой А. Укажите это число.

Закончив исследования, мы переходим в следующую лабораторию «Лабораторию раскрытия тайн».

Представьте себе, что ученые нашли при раскопках таинственные манускрипты, содержащие неизвестные объекты, и обратились к вам за помощью, чтобы вы разгадали эти таинственные знаки.

Перед вами равенства, содержащие неизвестное под знаком корня.

Определите, что там должно быть записано. Так как манускрипты старые и ветхие некоторые числа стерлись от времени. Ваша задача – восстановить запись.

Лаборатория раскрытия тайн

Найдите неизвестный объект

Проверяем правильные ответы на экране и объясняем, как были найдены неизвестные числа.

В оценочный лист ставите баллы, соответствующие числу правильных ответов.

Мы с вами поработали во всех лабораториях, а теперь немного отдохнем и посмотрим некоторые математические фокусы.

Это интересно.

Есть много математических фокусов. Самым элегантным математическим фокусом является возведение в квадрат чисел, оканчивающихся цифрой 5.

Проведем соответствующие рассуждения для числа 85 .

85² = 7225

Как быстро получить такой результат? Заметим, что достаточно 8 умножить на следующее за ним натуральное число 9, и мы получим 72, т.е. первые две цифры результата. Теперь достаточно приписать к полученному числу 25 и получается 7225, а это и есть ответ.

Проведем такую же операцию с числом 35.

35²=1225.

3*4=12 и приписываем 25.

Проверим этот фокус на числах 15 и 25. Вы знаете, какое число должно получиться при возведении этих чисел в квадрат.

Теперь перейдем в «Лабораторию практиков».

Каждый сотрудник пересаживается за компьютер, где уже подготовлены он-лайн тесты. Результаты теста переносим в оценочный лист. (тест разработан педагогом в программе MyTest)

Перед вами самая сложная лаборатория «Лаборатория эрудитов», требующая от вас умения правильно применять свои знания.

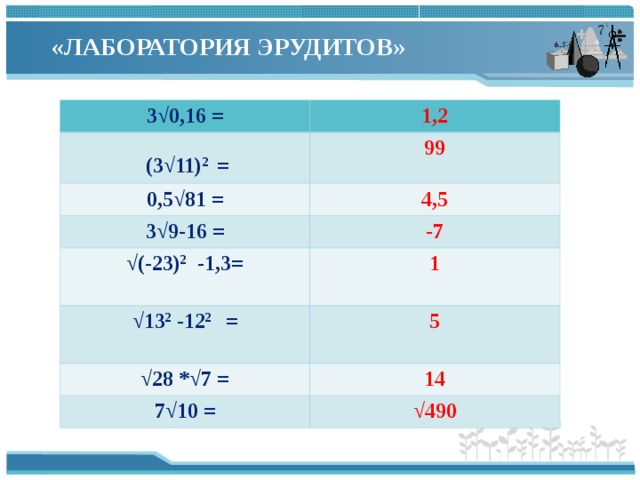
Лаборатория эрудитов

Итак, за работу в лаборатории эрудитов можно получить максимальную оценку 8 баллов (по числу правильных ответов). Ваша задача оценить свою работу в этой лаборатории (количество баллов должно соответствовать числу правильно решенных примеров).

Итоги урока

Подсчитываем в оценочном листе итоговое количество баллов и выставляем оценки.

Рефлексия.

Выбери один из вариантов.

1. Мне на уроке было интересно.

2. Мне на уроке было не интересно.

3. Я ушел с урока с хорошим настроением.

4. Я ушел с урока с плохим настроением.

Домашнее задание:

Повторить определение квадратного корня, свойства арифметического квадратного корня;

Выполните упражнения: №64 3),4); №65 1),3) №67 1),3)

Муниципальное казённое общеобразовательное учреждение средняя общеобразовательная школа № 3

Урок алгебры

в 8 «Б» классе по теме: «Арифметический корень и его свойства»

Проводит:

учитель математики

Калинина Е.Ю.

«ЛАБОРАТОРИЯ ТЕОРЕТИКОВ»

• I .Арифметическим квадратным корнем из числа а называется ______________число, квадрат которого равен а.

1.Неположительное 2.Неотрицательное 3.Положительное 4.Отрицательное

II . Квадратным корнем из числа а называют число, _______которого равен а

• 1.куб 2. корень 3. квадрат 4. площадь
• III . Уравнение вида х 2 = а не имеет корней, если
• 1. а=0 2. а≤ 0 3.а ‹ 0 4.а ≥ 0
• IV . На каком из рисунков изображен график функции  ?

«ЛАБОРАТОРИЯ ТЕОРЕТИКОВ»

1

2

2

3

3

3

4

2

«ЛАБОРАТОРИЯ ИССЛЕДОВАНИЙ»

«ЛАБОРАТОРИЯ РАСКРЫТИЯ ТАЙН»

• Найдите неизвестный объект

• I группа II группа

III группа

√ + 9 =15

√ - 3 = 7

2√ - 4=18

3√ - 5 = 31

13 - √ =10

21+√ =25

√ +6 = 10

3√ - 3=27

15 - √ = 6

«ЛАБОРАТОРИЯ РАСКРЫТИЯ ТАЙН»

• Найдите неизвестный объект

• I группа II группа

III группа

√ - 3 = 7

√ + 9 =15

3√ - 5 = 31

√ 100 - 3 = 7

2√ - 4=18

√ 36 + 9 =15

2√121 - 4=18

3√144 - 5 = 31

13 - √ =10

21+√ =25

13 - √9 =10

21+√16 =25

√ +6 = 10

3√ - 3=27

√ 16 +6 = 10

15 - √ = 6

3√100 - 3=27

15 - √81 = 6

МАТЕМАТИЧЕСКИЕ ФОКУСЫ

• 85 2 =7225
• 35 2 = 1225
• 3*4=12 и приписываем 25.

• Проверим этот фокус на числах 15 и 25

«ЛАБОРАТОРИЯ ЭРУДИТОВ»

3√0,16 =

(3√11) 2 =

0,5√81 =

3√9-16 =

√ (-23) 2 -1,3=

√ 13 2 -12 2 =

√ 28 *√7 =

7√10 =

«ЛАБОРАТОРИЯ ЭРУДИТОВ»

3√0,16 =

1,2

(3√11) 2 =

99

0,5√81 =

4,5

3√9-16 =

-7

√ (-23) 2 -1,3=

1

√ 13 2 -12 2 =

5

√ 28 *√7 =

14

7√10 =

√ 490

• Оценка «5» 22-26 баллов
• Оценка «4» 15-21 баллов
• Оценка «3» ниже 15 баллов