Открытый урок по теме: «Признаки равенства треугольников»

Открытый урок по теме: «Признаки равенства треугольников»

Цели:

Образовательные:

• повторить все признаки равенства треугольников и свойства равнобедренного треугольника;

• вырабатывать умения решать задачи с применением этих признаков.

Развивающая:

• развивать логическое мышление, внимание, быстроту реакций.

Воспитательная:

• воспитывать ответственное отношение к учебе.

Ход урока

1. Организационный момент.

Проверка готовности к уроку (наличие чертежных инструментов)

1. Актуализация знаний.

«Аквариум» (повторение теоретического материала). Приложение №1. Учащиеся объединены в 4 «домашние» группы по 3 человека. Каждая группа получает задание по раскрытию теоретического материала и использование его для решения задач.

Вопросы группам:

1. Первый признак равенства треугольника. Задача №1.

2. Второй признак равенства треугольника. Задача №2.

3. Третий признак равенства треугольника. Задача №3.

4. Равнобедренный треугольник. Задача №4.

1. Закрепление раннее изученного материала.

«Ажурная пилка» (практикум по решению задач).

Каждая группа идентифицируется определенным цветом, и каждый ученик в группе имеет карточку с порядковым номером от 1 до 3. Группа получает перечень задач, решаемых на уроке, и решают задачу своего цвета. На решение задач отводится 5 минут. По истечению отведенного времени учащиеся объединяются в «экспертные» группы, где каждый учащийся становится экспертом по решению своей задачи и объясняет ее решение ученикам своей группы. Таким образом, в новой группе учащиеся знакомятся с решением всех заданий данных группам на уроке. На эту работу отводится 10 минут. После завершения, учащиеся возвращаются в свои «домашние» группы и преступают к выполнению самостоятельной работы.

1. Контроль знаний.

Самостоятельная работа.

Учащиеся решают в рабочих тетрадях задачу своей группы и одну из понравившихся задач другой группы.

1. Домашнее задание. Разгадайте кроссворд. Приложение №2.

2. Рефлексия:

• Сегодня на уроке, я понял/а…

• При решении геометрических задач, необходимо…

• Самое трудное для меня…

• А теперь оцените собственную работу, групп.

Описание интерактивных технологий, используемых на уроке математике

1. «Аквариум»

Данная технология используется для повторения теоретического материала

Описание технологии:

1. Учащиеся объединены в 4 «домашние» группы по 3 человека. Каждая группа получает задание по раскрытию теоретического материала и использование его для решения задач.

2. Группы по очереди занимают место у доски, читают задание и в течении 3-4 минут обговаривают теоретической материал и возможные варианты решения предложенных задач.

3. Остальные учащиеся слушают и не вмешиваются в рассуждения.

4. По истечению отведенного времени, группа возвращается на свои места, а класс должен ответить на вопросы:

• Согласны ли вы с ответами?

• Были ли они полными и аргументированными?

1. Оценивается работа всей группы. При этом учитывается полнота ответов, а также активность всех членов группы.

2. Оценка за теоретический материал складывается из оценки группы, к которой добавляются баллы за личную активность каждого при обсуждении ответов других групп.

1. «Ажурная пилка»

Эта технология используется для проведения практикума по решению задач.

Описание технологии:

1. Объединение учащихся в группы такое же, что и в технологии «Аквариум».

2. Каждая группа идентифицируется определенным цветом, и каждый ученик в группе имеет карточки с порядковым номером от 1 до 3.

3. Каждый ученик получает перечень задач, решаемых на уроке.

4. Группам указывается, какие из перечисленных задач они должны презентовать. На решение задач отводится 5 минут.

5. По истечении отведенного времени учащиеся объединяются в «экспертные» группы. Так учащиеся под номером 1 объединяются в группу под номером 1 и т.д. Так образуются 3 новые группы по 4 человека, где каждый учащийся становится экспертов по своей части информации и делит ее со всеми участниками своей группы. Таким образом, в новой группе учащиеся знакомятся с решением всех заданий данных группам на уроке. На эту работу отводится 10 минут.

6. После завершения работы, учащиеся возвращаются в свои «домашние» группы, обмениваются информацией, полученной в «экспертной» группе, и затем каждая группа презентует на доске свое решение.

7. Учащиеся самостоятельно выполняют записи в тетрадях, следя за ходом решения задачи на доске, дополняя ответы.

Приложение №1.

Задача №1.

На рисунке

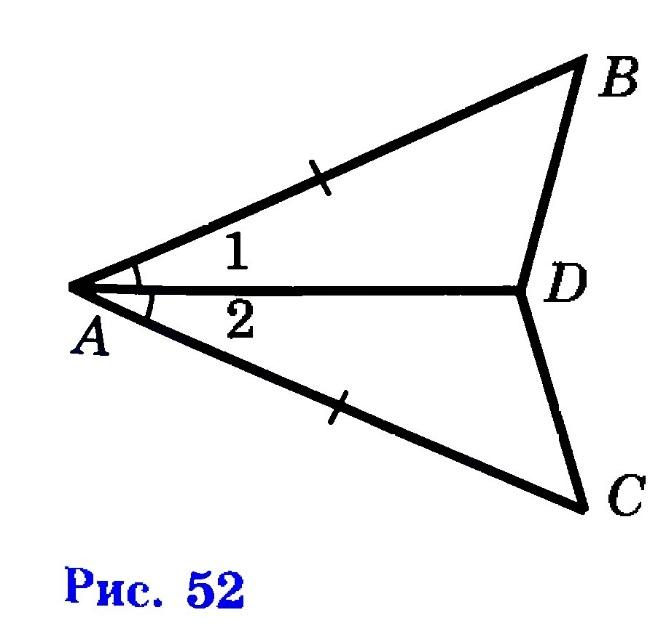
AB=AC;

а) Докажите: ΔABD =ΔACD.

б) Найдите: BD и AB, если

AC=15 см, DC=5 см

Задача №2.

L М На рисунке:

KO=OM;

O a) Докажите: ΔKOL = ΔMON.

б) Найдите: MN и ON, если

K N KL =8 см; OL= 5 см.

Приложение №1.1

Задача №3.

B C На рисунке:

AB=CD; BC=DA

а) Докажите: ΔABC = ΔCDA.

б)

A D

D Задача №4.

O

На рисунке:

LD=DN,

а) Докажите: ΔDLO =ΔDNO.

б) Найдите: LO и ND, если

ON = 9 см; LD = 18 см.

Приложение №3.

Кроссворд:

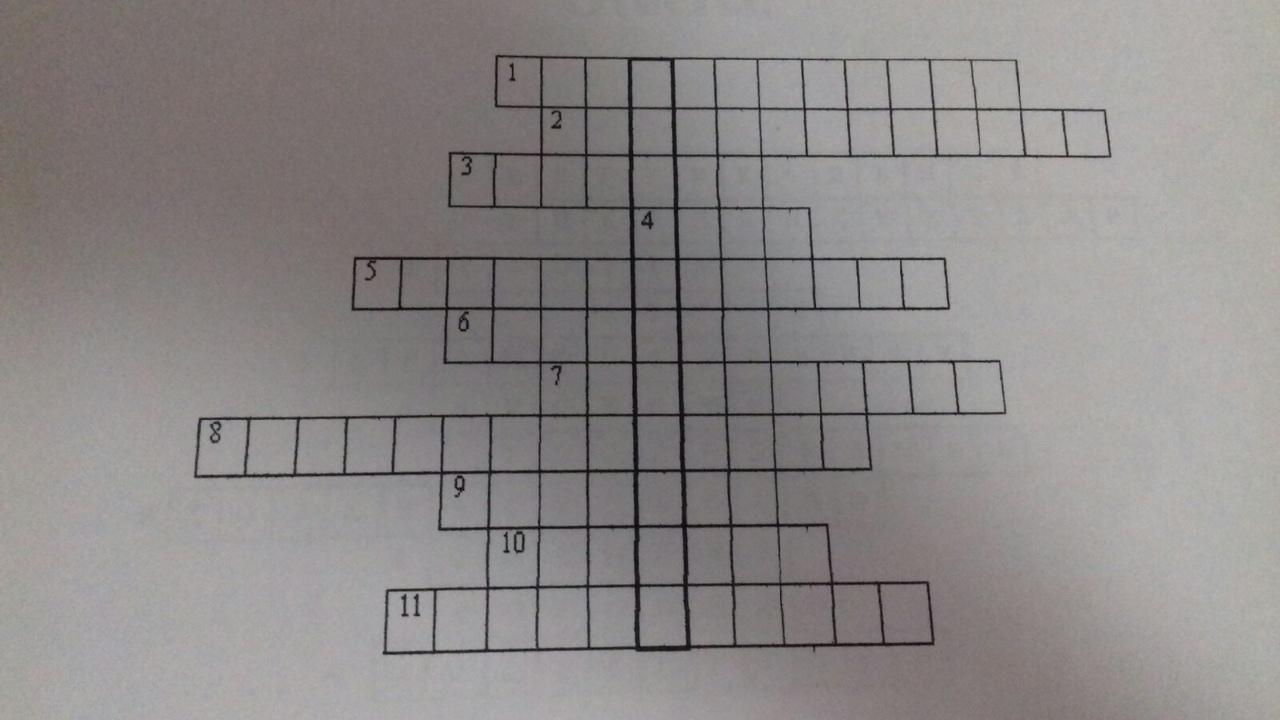
1. Углы, стороны которых являются дополнительными полупрямыми.

2. Отрезок прямой, перпендикулярный к данной прямой с концом на этой прямой.

3. Утверждение о свойствах фигур, которые необходимо доказывать.

4. Геометрическая фигура из двух лучей с общим началом.

5. Четырехугольник, у которого все углы – прямые.

6. Утверждение о свойствах фигур, которые принимают без доказательства.

7. Части, на которые точка делит любую прямую.

8. Строгое логическое рассуждение.

9. Углы, имеющие общую сторону, а другие стороны – дополнительные полупрямые.

10. Отрезок, соединяющий вершину треугольника с серединой противоположной стороны.

11. Луч, выходящий из вершины угла, проходящий между его сторонами. Делящий угол на две равные части.

Ответы: