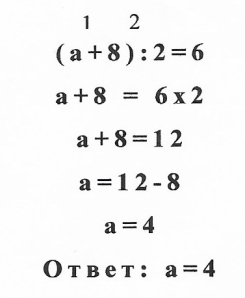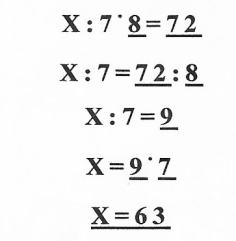Открытый урок по математике: "Решение сложных уравнений"

Открытый урок по математике

в 3 классе

Учитель: Шеварнова Т.Н.

Тип урока: ОНЗ.

Тема: «Решение сложных уравнений»

2021г.

Цель урока:

- дать понятие о сложном уравнении и отличии его от простого;

- составить алгоритм решения сложного уравнения;

- развивать умение логически анализировать задание;

- развивать умение планировать деятельность;

- развивать устную математическую речь учащихся.

Ход урока:

1. Организационный момент.

- У нас в гостях математические человечки — знаки арифметических

действий. Они снова приглашают нас в ИКС-педицию.

- Что такое ИКС-педиция? (путешествие, с целью поиска неизвестного —

икса).

- Как вы думаете, чем мы сегодня будем заниматься? (решать уравнения).

- Что называется уравнением? (уравнение — это равенство, содержащее

переменную, значение которой надо найти).

2. Актуализация знаний.

Чтобы проверить вашу готовность человечки предлагают выполнить

следующие задания:

1) 4+8:(12-8) х 3=

- Какое действие выполним первым? Вторым? и т. д.

(дети поднимают карточки со знаками арифметических действий).

- Найдите значение выражения (10).

2) Из данных математических записей назовите уравнения:

у: 9= 60

х : 10 +419

Вариант конспекта урока по математике (начальная школа) для апробации на экспериментальных площадках ассоциации «Школа 2000...»

с — 30 = 35 + 50

у - 7 10

( дети называют у : 9 = 60 и с- 30 = 35 + 50)

- Как называется выражение в левой части? (частное; разность).

3) Выберите число, которое является корнем уравнения

у:9= 60 ( 540 630) с -30=35 + 50 ( 55 115)

(Дети показывают цвет, соответствующий правильному ответу)

- Как нашли корень уравнения? Какие «шаги» для этого сделали?

(Дети рассказывают ход решения уравнения, в соответствии с алгоритмом)

Алгоритм решения простых уравнений

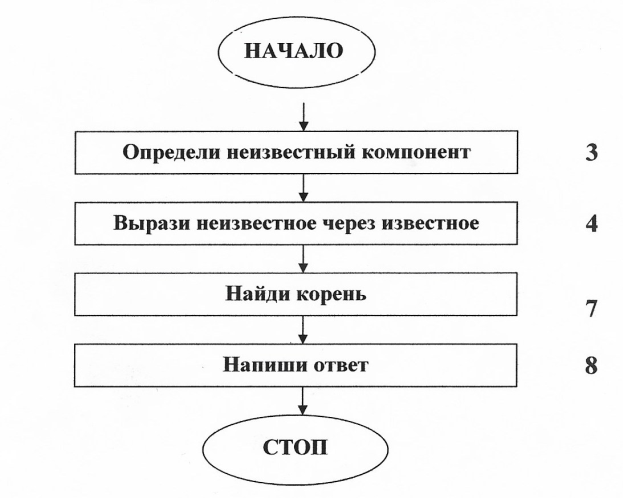
4) Составьте, запишите и решите уравнение с неизвестным слагаемым (Дети записывают в левой части страницы тетради уравнение и решают его).

Вариант конспекта урока по математике (начальная школа)

для апробации на экспериментальных площадках

ассоциации «Школа 2000...»

- Какой компонент был неизвестен? (1 слагаемое, 2 слагаемое)

- Как найти неизвестное слагаемое? (чтобы найти неизвестное

слагаемое нужно от суммы отнять известное слагаемое)

5) Составьте, запишите и решите уравнение по данному условию и

вопросу:

У Коли а слив, у Миши — 8 слив. Они сложили их и все сливы поделили

поровну. У каждого оказалось по 6 слив. Сколько слив было у Коли?

(Дети записывают в правой части страницы тетради уравнение (а+8): 2 =6 )

3. Постановка проблемы

- Решили уравнение? (Да, Нет)

- Назовите корень уравнения? (4; 2;?)

- В чем возникла трудность? Почему?

(Не смогли найти корень уравнения, потому что не умеем решать такие

уравнения)

- А какие уравнения умеем решать? (Простые)

- Можно ли назвать данное уравнение простым? (Нет)

- Как мы назовем подобное уравнение? (Сложным)

- Помог ли вам алгоритм, по которому вы сегодня решали уравнения?

(Нет)

- Что же нам сегодня надо узнать? (Как решать сложные уравнения)

- Что для этого нужно сделать? (Составить новый алгоритм)

На доске появляется запись темы урока: «Решение сложных уравнений».

4. Физ.-минутка.

Дети под ритмичную музыку хором говорят речевку и выполняют

танцевальные движения

Шагает дружно 3 «А»,

С задачей справится всегда.

Иди вперед смелей, не пой

И алгоритм построишь свой!

5. Открытие «нового» знания. (Дополнение алгоритма)

1) - Как мы решали простые уравнения?

(Дети еще раз проговаривают «шаги» алгоритма решения простых уравнений)

- Можно ли решить новое уравнение, используя связь между компонентами? (Можно)

Чем осложнен поиск неизвестного компонента? (В левой части 2 действия)

- Как узнать, каким компонентом является неизвестное число в нашем уравнении? (Надо найти действие, которое привело к результату)

- Что для этого надо сделать с выражением в левой части?

(Определить порядок действий и выделить последнее действие).

Один ученик у доски, остальные учащиеся на местах составляют цветовую модель уравнения: последнее действие выделяют желтым цветом, неизвестный компонент — красным, известные —зеленым.

- Как назовете выражение в левой части? (Частное)

- Что неизвестно? (Делимое)

- Выполните следующий шаг алгоритма

- Можем найти корень? ( Нет. Надо упростить правую часть)

- Можем теперь найти корень? (Да. Получили простое уравнение)

- Дальше решаем по алгоритму как простое уравнение

- Сколько действий пришлось выполнить для решения уравнения? (3).

2) Запишите решение уравнения, с опорой на цветовую модель и новый алгоритм.

(1 ученик у доски проговаривает решение уравнения и записывает его ход)

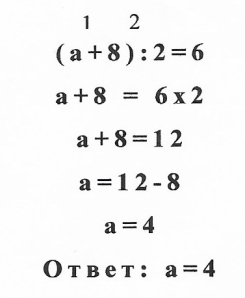
4. Первичное закрепление

1) составить цветовую модель решения уравнения

х:7х8=72

(Дети с помощью геометрических фигур, в парах, составляют

модели, 1 ученик выполняет задание у доски с проговариванием)

2) Запись решения уравнения с опорой на цветовую модель.

(Дети подчеркивают компоненты соответственным цветом: неизвестное-

красным; известное — зеленым).

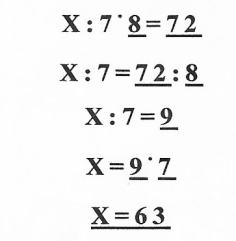
3) Самостоятельное решение уравнения с самопроверкой

35: (15-у)=7

Сверьте ход решения с алгоритмом и отметьте правильно выполненные шаги знаки «+» соответствующей строки решения.

1 2

35: (15-у)=7 (Шаги 1,2,3)

1. Записать уравнения, соответствующие данной схеме, вставив пропущенные знаки действий

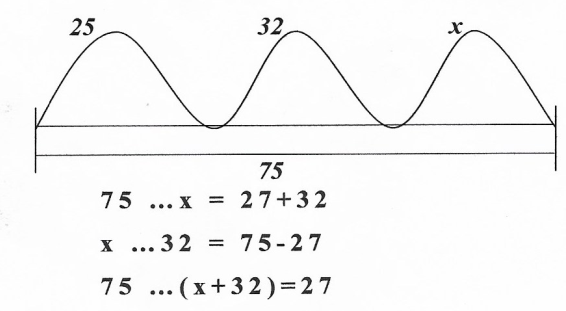
- Назовите уравнение нового вида?

75 - (х+32)=27

- Составьте план решения этого уравнения.

8. Домашнее задание

- Запишите и решите уравнение дома и составьте для одноклассников

сложное уравнение подобного вида

9. Итог урока:

- Что нового узнали на уроке? Чему научились? Как бы вы оценили свою работу на уроке.

(Дети оценивают себя с помощью светофорчиков: красный-зеленый)