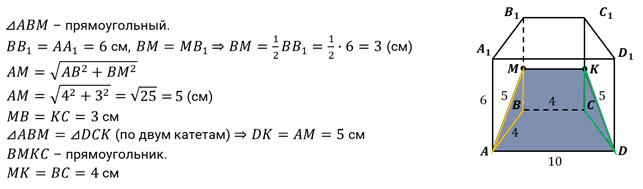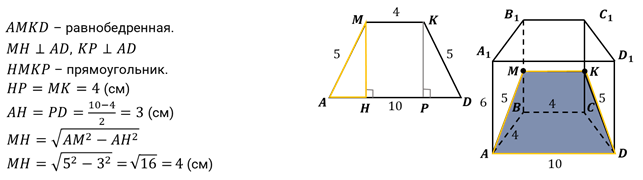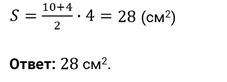Тема: Симметрия в кубе, в параллелепипеде, в призме и пирамиде. Сечения куба, призмы и пирамиды.
-
Симметрия в кубе, в параллелепипеде, в призме и пирамиде.
Симметрия в переводе с греческого означает «соразмерность» (повторяемость). Симметричные тела и предметы состоят из равнозначных, правильно повторяющихся в пространстве частей. Особенно разнообразна симметрия кристаллов. Различные кристаллы отличаются большей или меньшей симметричностью. Она является их важнейшим и специфическим свойством, отражающим закономерность внутреннего строения.
Симметрия – это закономерная повторяемость элементов (или частей) фигуры или какого-либо тела, при которой фигура совмещается сама с собой при некоторых преобразованиях (вращение вокруг оси, отражение в плоскости).
Понятие симметрии включает в себя составные части – элементы симметрии. Сюда относятся плоскость симметрии, ось симметрии, центр симметрии.
Ось симметрии – воображаемая ось, при повороте вокруг которой на некоторый угол, фигура совмещается сама с собой в пространстве.
Центр симметрии – это точка внутри многогранника, в которой пересекаются и делятся пополам прямые, соединяющие одинаковые элементы многогранника (грани, ребра, углы).
Плоскость симметрии делит многогранник на 2 зеркально равные части.
Степенью симметрии называется совокупность всех элементов симметрии, которыми обладает данный многогранник.
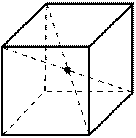
Центр симметрии (центр куба) – точка пересечения диагоналей куба.
Плоскости симметрии (9): 3 плоскости симметрии, проходящие через середины параллельных ребер (первая строчка); 6 плоскостей симметрии, проходящие через противолежащие ребра (вторая строчка).

Ось симметрии (13): 3 оси, проходящие через центры противолежащих граней; 4 оси симметрии, проходящие через противолежащие вершины; 6 осей, проходящие через середины противолежащих ребер.

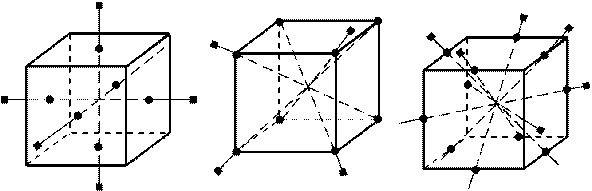
Центр симметрии – точка пересечения диагоналей прямоугольного параллелепипеда.
Плоскость симметрии: 3 плоскости симметрии, проходящие через середины параллельных рёбер.
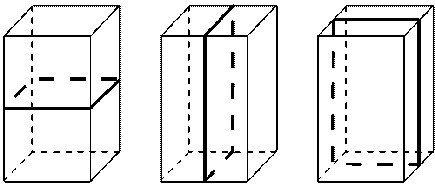
Ось симметрии: 3 оси симметрии, проходящие через точки пересечения диагоналей противолежащих граней.
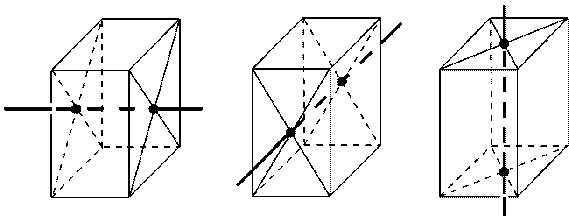
- симметрия прямой призмы: одна плоскость симметрии, проходящая через середины боковых рёбер.
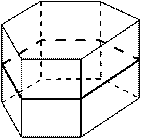
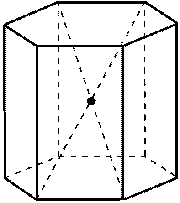 - симметрия правильной призмы.
- симметрия правильной призмы.
Центр симметрии: при чётном числе сторон основания центр симметрии – это точка пересечения диагоналей правильной призмы.
Плоскости симметрии: плоскость, проходящая через середины боковых рёбер; при чётном числе сторон основания – плоскости, проходящие через противолежащие рёбра.
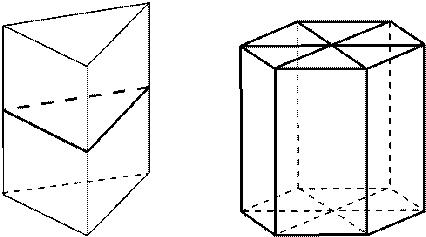
Ось симметрии: при чётном числе сторон основания – ось симметрии проходит через центры оснований; оси симметрии, проходящие через точки пересечения диагоналей противолежащих боковых граней.
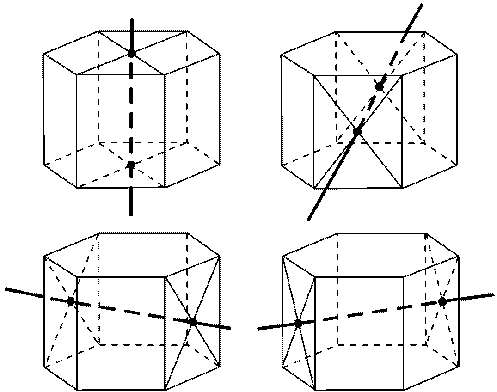

Плоскости симметрии: при четном числе сторон основания – плоскости, проходящие через противолежащие боковые ребра и плоскости, проходящие через медианы, приведенные к основанию противолежащих боковых граней.
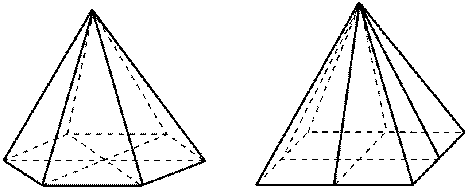
Ось симметрии: при четном числе сторон основания – ось симметрии проходит через вершину правильной пирамиды и центр основания.
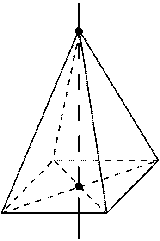
-
Сечения куба, призмы и пирамиды.
Секущей плоскостью называют любую плоскость, по обе стороны от которой имеются точки данной фигуры.
Секущая плоскость пересекает грани многогранника по отрезкам.
Многоугольник, сторонами которого являются эти отрезки, называется сечением многогранника.

Построить сечение многогранника плоскостью – это значит указать точки пересечения секущей плоскости с рёбрами многогранника и соединить эти точки отрезками, принадлежащими граням многогранника.
Теперь давайте вспомним, что нам необходимо знать для построения плоскости. Итак, построить плоскость можно: с помощью трёх точек, не лежащих на одной прямой;

с помощью двух пересекающихся прямых;

с помощью прямой и точки, которая не лежит на прямой;

а также с помощью двух параллельных прямых.

| Основные методы построения сечений многогранников |
| Метод следов | Метод вспомогательных сечений | Комбинированный метод |
Метод следов включает три важных пункта: сначала нужно построить линию пересечения (след) секущей плоскости с плоскостью основания многогранника; затем найти точки пересечения секущей плоскости с рёбрами многогранника, а после этого построить и заштриховать сечение. В основе построения сечения методом следов лежат две теоремы:
- если две точки прямой принадлежат плоскости, то и вся прямая принадлежит плоскости;
- если плоскость проходит через прямую, параллельную другой плоскости, и эти плоскости пересекаются, то линия их пересечения параллельна первой прямой.
Метод вспомогательных сечений применяется при построении сечений в тех случаях, когда неудобно находить след секущей плоскости. Например, след получается очень далеко от заданной фигуры.
Комбинированный метод суть построения сечений многогранников состоит в применении теорем о параллельности прямых и плоскостей в пространстве в сочетании с методом следов или методом вспомогательных сечений.
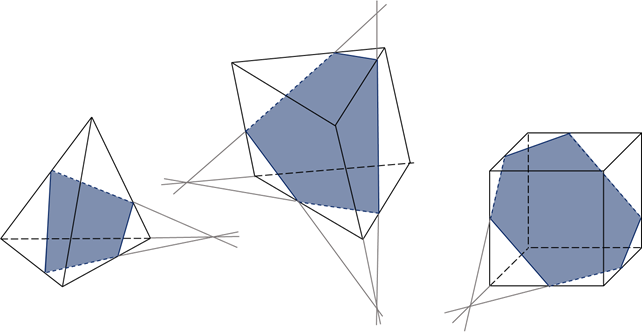
Обратите внимание: тетраэдр имеет четыре грани, поэтому его сечениями могут быть только треугольники и четырёхугольники. А вот параллелепипед имеет шесть граней, поэтому его сечениями могут быть треугольники, четырёхугольники, пятиугольники и шестиугольники.

Практическая часть
Задача 1. В основании прямой призмы лежит равнобедренная трапеция с основаниями равными 10 см и 4 см, и боковой стороной, равной 4 см. Боковое ребро призмы равно 6 см. Найдите площадь сечения призмы плоскостью, проходящей через большую сторону основания и середин противоположного бокового ребра призмы.
Дано:

Решение:
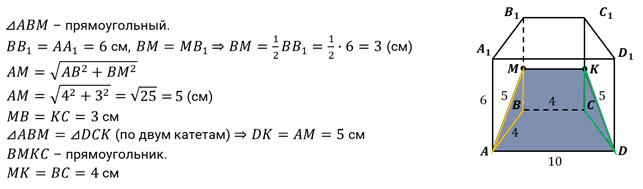
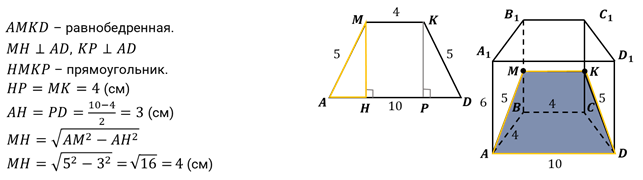
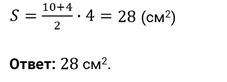
Задача 2. На ребре AD правильного тетраэдра DABC с длиной ребра, а взята точка М такая, что МА:МD = 3:1. Найдите площадь сечения тетраэдра плоскостью, содержащей точку М и перпендикулярной ребру AD.
Решение:

Задача 3. В основании четырёхугольной пирамиды SABCD лежит квадрат ABCD, а две боковые грани SBA и SAD представляют собой прямоугольные треугольники с прямым  А. Найдите площадь сечения пирамиды плоскостью, содержащей точку пересечения диагоналей основания и параллельной грани SBC, если SA = AB = a.
А. Найдите площадь сечения пирамиды плоскостью, содержащей точку пересечения диагоналей основания и параллельной грани SBC, если SA = AB = a.
Решение:
Задание:
Задача 1. В основании прямой призмы лежит равнобедренная трапеция с основаниями равными 20 см и 8 см, и боковой стороной, равной 8 см. Боковое ребро призмы равно 12 см. Найдите площадь сечения призмы плоскостью, проходящей через большую сторону основания и середин противоположного бокового ребра призмы.
Задача 2. Заполнить таблицу «Правильные многогранники»
| Определение правильного многогранника | Изображение | Число граней (Г) | Число вершин (В) | Число рёбер (Р) | Форма грани | Число граней, сходящихся в одной вершине | Сумма плоских углов при вершине |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Тетраэдр - |
|
|
|
|
|
|
|
| Куб (гексаэдр) - |
|
|
|
|
|
|
|
| Октаэдр - |
|
|
|
|
|
|
|
| Икосаэдр - |
|
|
|
|
|
|
|
| Додекаэдр - |
|
|
|
|
|
|
|
Примечание: графа 1 написать определение каждого многогранника, графа 2 изображение зарисовать, графы 3 – 8 записать цифрами.
Ребята, выполняем все задания и все ребята (а не два человека с группы, присылаем, я все отмечаю, кто отчитался и сколько отчитался), ведомость мы все равно заполняем и будем подавать сведения, поэтому никто без внимания не останется.
Прошу присланные ваши сообщения, письма, подписывать: ФИ, группа, предмет, за какое число. СПАСИБО












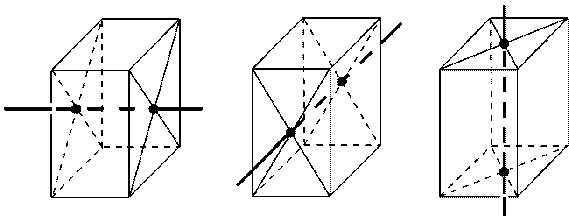

 - симметрия правильной призмы.
- симметрия правильной призмы.