Просмотр содержимого документа
«Параллельность прямых и плоскостей в пространстве»
Инструкционная карта № 23
Тақырыбы/ Тема: Решение задач по теме: «Параллельность прямых и плоскостей в пространстве».
Мақсаты/ Цель:
Уметь применять определения, признаки и свойства параллельных прямых и плоскостей в пространстве при решении задач.
Создать условия для развития умения устанавливать единые общие признаки и свойства целого, составлять план деятельности при решении задач.
Воспитание личностных качеств посредством развития индивидуальных познавательных интересов и способностей.
Теоретический материал:
1.Определение. Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.
 b||а
b||а
2. Определение: Прямая и плоскость называются параллельными ,
если они не имеют общих точек.

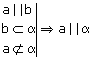
3. Определение: Плоскости называются параллельными, если они не пересекаются.

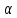 ||
||  .
.
Теорема: (признак параллельности прямых в пространстве) Две прямые , параллельные третьей прямой, параллельны.
Теорема: (признак параллельности прямой и плоскости) Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна самой плоскости.
Теорема: (признак параллельности плоскостей) Если две пересекающиеся прямые одной плоскости параллельны двум прямым другой плоскости, то эти плоскости параллельны.
| 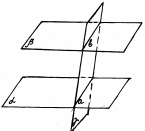
| Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны.
|
| 
| Отрезки параллельных прямых между параллельными плоскостями равны.
|
1. Задача. Дано: 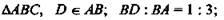
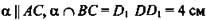 (рис. 2).
(рис. 2).
Доказать: ΔDBD1 ~ ΔABC.
Найти: AC.
Решение:
1)  - по признаку, значит,
- по признаку, значит, 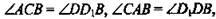 ∠B - общий для ΔАВС и ΔDBD1. Следовательно, ΔDBD1 ~ ΔАВС.
∠B - общий для ΔАВС и ΔDBD1. Следовательно, ΔDBD1 ~ ΔАВС.
2) Из ΔABC ~ ΔDBD1 ⇒ 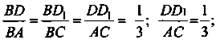
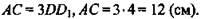 (Ответ: 12 см.)
(Ответ: 12 см.)
2.Задача. Через конец А отрезка АВ проведена плоскость, а через конец В и точку С этого отрезка проведены параллельные прямые, пересекающие данную плоскость в точках В1 и С1 соответственно. Найдите длину отрезка СС1, если ВВ1 = 18 см и АВ1 : С1В1 = 3 : 1.
 Дано: А
Дано: А В
В С
С
ВВ1 СС1, ВВ1 = 18 см
СС1, ВВ1 = 18 см


 АВ1 : С1В1 = 3 : 1.
АВ1 : С1В1 = 3 : 1.
 Найти: СС1
Найти: СС1
![]()
Решение:
Рассмотрим  АСС1 и
АСС1 и  АВВ1, они подобны, т.к.
АВВ1, они подобны, т.к.  А-общий и
А-общий и  С=
С= В как соответственные при параллельных прямых ВВ1
В как соответственные при параллельных прямых ВВ1 СС1 и секущей АВ. Тогда стороны пропорциональны по признакам подобия треугольников.
СС1 и секущей АВ. Тогда стороны пропорциональны по признакам подобия треугольников.

 =
=  ;
; 
 = 12(см) Ответ:
= 12(см) Ответ:  12см
12см
Задача 3. Через точку К, не лежащую между параллельными плоскостями α и β, проведены прямые l и m. Прямая l пересекает плоскости α и β в точках A1 и A2 соответственно, прямая m – в точках B1 и B2.
Найдите длину отрезка A2B2, если KA1 : A1A2 = 2 : 3, A1B1 = 8 см.




Дано:  К
К , К
, К

 A1,
A1,  B1, m
B1, m A2, m
A2, m B2
B2
KA1 : A1A2 = 2 : 3, A1B1 = 8 см
Найти: A2B2

![]()



![]()


Решение:
Рассмотрим  КА1В1 и
КА1В1 и  КА2В2, они подобны (см. решение предыдущей задачи). Значит, стороны пропорциональны. Составим пропорцию
КА2В2, они подобны (см. решение предыдущей задачи). Значит, стороны пропорциональны. Составим пропорцию  ,
,  ,
,
 =
=  = 20 (см). Ответ:
= 20 (см). Ответ:  = 20см
= 20см
Задача 4. Прямая  пересекает параллельные плоскости
пересекает параллельные плоскости  в точках А и В. Прямая
в точках А и В. Прямая  , параллельная прямой
, параллельная прямой  , пересекает эти плоскости в точках С и D. Чему равен отрезок СD, если: АВ=13см.
, пересекает эти плоскости в точках С и D. Чему равен отрезок СD, если: АВ=13см.



![]()
Дано: 



 A,
A,  B,
B,  С,
С, 
АВ=13см.

Найти: СD
![]()


Решение:
Рассмотрим четырехугольник АВ С – параллелограмм, т.к.
С – параллелограмм, т.к.  и по второму свойству
и по второму свойству
параллельности плоскостей АС В
В и равны между собой. Следовательно СD= АВ=13см.
и равны между собой. Следовательно СD= АВ=13см.
Ответ: СD= 13см.
Практическая часть:
| 1 вариант | 2 вариант | 3 вариант | 4 вариант |
Через концы отрезка АВ и его середину М проведены параллельные прямые, пересекающие некоторую плоскость в точках А1, В1, М1. Найдите длину отрезка ММ1, если отрезок АВ не пересекает плоскость и если: |
| АА1= 6 м, ВВ1= 7 м. | АА1= 4.5 м, ВВ1=3.7 м. | АА1=1.4 м, ВВ1= 5.6 м. | АА1= 8.1м, ВВ1=5.4 м. |
Через конец А отрезка АВ проведена плоскость. Через конец В и точку С этого отрезка проведены параллельные прямые, пересекающие плоскость в точках В1 и С1. Найдите длину отрезка ВВ1, если: |
| СС1=10см, АС =3:2 =3:2 | СС1=2,7см, АВ:АС=12:9
| АВ=6см, АС:СС1=2:5 | АВ=3см, ВС=5см, СС1=12см. |
Дан треугольник АВС. Плоскость, параллельная прямой АВ, пересекает сторону АС этого треугольника в точке А1, а сторону ВС – в точке В1. Найти длину отрезка А1В1, если: |
| АВ=10см, АА1:АС=2:5 | АВ=6см, АА1:А1С=6:4 | В1С=10см, АВ:ВС=4:5 | АА1=2,3см, АВ=12см, А1С=1,9см. |
| 4.Плоскости α и β параллельны между собой. Из точки М, которая не принадлежит этим плоскостям и не находится между ними, проведены два луча. Один из них пересекает эти плоскости α и β в точках А1 и В1, а другой –в точках А2 и В2 соответственно. Найдите длину отрезка В1В2, если он на 4 см больше отрезка А1А2, МВ1 = 9см, А1В1=6см. | 4.Плоскости α и β параллельны между собой. Из точки О, которая не принадлежит этим плоскостям и не находится между ними, проведены два луча. Один из них пересекает плоскости α и β в точках С1 и D1, а другой – в точках C2 и D2 соответственно. Найдите длину отрезка C1C2, если он на 3см меньше отрезка D1D2, ОС1 = 2см, С1D1=8см. | 4.Через точку О, лежащую между параллельными плоскостями α и β, проведены прямыеl и m. Прямая l пересекает плоскости α и β в точках А1 и А2 соответственно, прямая m – в точках В1 и В2. Найдите длину отрезка А2В2, если А1В1 = 12 см, В1О:ОВ2 = 3 : 4.
| 4.Через точку К, не лежащую между параллельными плоскостями α и β, проведены прямые а и b. Прямая а пересекает плоскости α и β в точках А1 и А2 соответственно, b – в точках В1 и В2.. Найти В1В2, если А2В2 : А1В1 = 9 : 4, КВ1 = 8см.
|
| 5.Даны две параллельные плоскости. Через точки А и В одной из этих параллельных плоскостей проведены параллельные прямые, пересекающие вторую плоскость в точках А1 и В1. Чему равен отрезок А1В1, если: | 5.Прямая  пересекает параллельные плоскости пересекает параллельные плоскости  в точках А и В. Прямая в точках А и В. Прямая  , параллельная прямой , параллельная прямой  , пересекает эти плоскости в точках С и D. Найдите периметр четырехугольника АВСD, если: , пересекает эти плоскости в точках С и D. Найдите периметр четырехугольника АВСD, если: |
| АВ = m | AB = n. | АВ=3см, АС=4см. | СD=5см, АС=7см. |
Контрольные вопросы:
Какие две прямые в пространстве называются параллельными?
Сформулируйте признак параллельности прямых в пространстве.
Какие прямая и плоскость называются параллельными?
Сформулируйте признак параллельности прямой и плоскости.
Какие две плоскости называются параллельными?
Сформулируйте признак параллельности плоскостей.
Сделайте геометрическую иллюстрацию свойств параллельности плоскостей в пространстве и сформулируйте их.







 b||а
b||а 
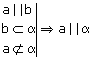

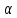 ||
||  .
.


 Дано: А
Дано: А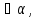 В
В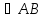
 СС1, ВВ1 = 18 см
СС1, ВВ1 = 18 см

 АВ1 : С1В1 = 3 : 1.
АВ1 : С1В1 = 3 : 1.  Найти: СС1
Найти: СС1









