Параллелограмм и его свойства

Урок 14: «Параллелограмм. Свойства параллелограмма»

Давайте вспомним...

Какие прямые называют параллельными?

Параллельными прямыми называют прямые, которые лежат в одной плоскости и не пересекаются

Какие многоугольники вам уже известны?

Треугольники, четырехугольники (прямоугольник, квадрат )

С помощью каких инструментов можно построить многоугольник и параллельные прямые?

С помощью линейки и чертежного треугольника

m

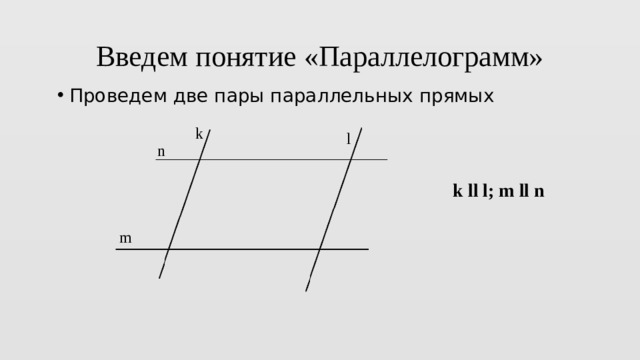
Введем понятие «Параллелограмм»

• Проведем две пары параллельных прямых

k

l

n

k ll l; m ll n

m

Параллелограмм

• При пересечении параллельных прямых k, l и m, n мы получили четырёхугольник, который называется параллелограммом

ОПРЕДЕЛЕНИЕ: Параллелограмм – это четырехугольник, противоположные стороны которого попарно параллельны

k

l

n

k ll l; m ll n

Эксперимент с калькой

• Параллелограмм является центрально-симметричной фигурой. Центр симметрии параллелограмма —точка пересечения диагоналей. Давайте убедимся в этом!

• Представим, что мы наложили на наш параллелограмм кальку
• Проткнули ее в точке пересечения диагоналей (точка О)
• Повернём кальку на 180 о
• Не трудно заметить, что при повороте калька «входит» в контур параллелограмма

О

C

B

A D

Эксперимент с калькой

• Рассмотрим ещё раз поворот кальки на 180 о
• Параллельные прямые отмечены разным цветом, при повороте стороны параллелограмма поменялись местами
• Делаем вывод, что противоположные стороны параллелограмма не только параллельны, но и равны

Эксперимент с калькой

• При этом же повороте закрашенный треугольник совмещается с белым
• Следовательно, диагональ делит параллелограмм на два равных треугольника.
• Диагонали заняли свои прежние места , значит диагонали точкой пересечения делятся пополам.

C

B

O

D

A

Итак, перечислим еще раз свойства параллелограмма:

• Противоположные стороны параллелограмма параллельны и равны
• Диагональ делит параллелограмм на два равных треугольника
• Диагонали точкой пересечения делятся пополам

Как построить параллелограмм? (включите видео)

1) Проведем две пересекающиеся прямые и обозначим точку их пересечения буквой О.

2) На одной из прямых отложим циркулем равные отрезки ОА и ОС, а на другой – равные отрезки OB и OD.

3) Соединим последовательно точки A, B, C и D отрезками.

Четырехугольник ABCD – параллелограмм.

На странице 206 (до абзаца «Виды параллелограммов») учебника МАТЕМАТИКА. Арифметика. Геометрия. Автора Е.А. Бунимович, вы можете познакомиться с темой «Параллелограмм и его свойства».

Выполним задание 1: Назовите все параллелограммы которые вы видите на рисунке.

Ответ: AFEB, AFDC, BEDC (можно идти в другом направлении, начиная с любой вершины, но, обязательно, попорядку,

т.е AFEB = ABEF = BEFA = FEBA =…)

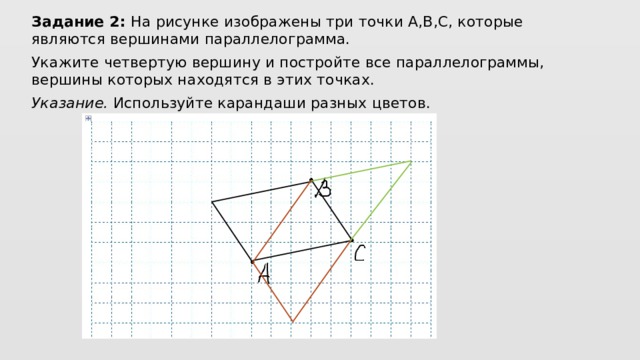
Задание 2: На рисунке изображены три точки A,B,C, которые являются вершинами параллелограмма.

Укажите четвертую вершину и постройте все параллелограммы, вершины которых находятся в этих точках.

Указание. Используйте карандаши разных цветов.

Что нового вы сегодня узнали? Продолжите фразы

Сегодня я узнал/ узнала …

Сегодня я научился/ научилась ...

Домашнее задание!

К следующему уроку: параграф 44, №685 устно, 686, 687

До скорой встречи.