Дата 14,03,23 Класс 9-Е,Ж,Б Шевель И.А, урок №98
Тема урока: Перестановка из n элементов конечного множества.
Тип урока: урок изучения нового материала.
Цели урока:
-
образовательные: рассмотреть с учащимися определение перестановки из n элементов; ознакомить учащихся с формулой подсчета числа всевозможных перестановок из n элементов и научить применять её при решении соответствующих комбинаторных задач;
-
развивающие: способствовать развитию математической речи; развивать умение переводить информацию из одного представления в другое;
-
воспитательные: формировать интерес к предмету; развивать аккуратность.
Планируемые результаты: понимать смысл понятия перестановки; умение использовать формулу при решении задач и строить речевые высказывания; умение устанавливать закономерность
Личностные УУД: умение устанавливать связи между целью учебной деятельности и её мотивом; умение развивать интеллектуальные способности, логическое мышление в процессе решения задач, сравнивать, выявлять закономерности, обобщать; формирование ценностных отношений друг к другу, учителю, результатам обучения. Метапредметные: умение определять и формулировать цель на уроке с помощью учителя; проговаривать последовательность действий на уроке; оценивать правильность выполнения действия; умение оформлять свои мысли в устной форме; слушать и понимать речь других; Предметные: умение применять изученные понятия, результаты, методы для решения задач практического характера. Уметь находить факториал и количество перестановок. овладение навыками устных, письменных, инструментальных вычислений.
Оборудование: доска, учебник, презентация и видео, пк
Распределение урока во времени:
-
Организационный момент – 3 минуты.
-
Изучение нового материала – 15 минут.
-
Закрепление изученного материала – 19 минут.
-
Подведение итогов – 5 минут.
-
Домашнее задание – 3 минуты.
Ход урока.
| Деятельность учителя | Деятельность учащихся |
| 1. Организационный момент Приветствие, проверка подготовленности к учебному занятию, организация внимания детей, проверка дз, отсутствующие 2.Актуализация 1) Вспомнить комбинаторное правило умножения 2) Какие события называются однозначными? Как вы это понимаете? Приведите примеры. Однозначными называются события, которые имеют заранее определённый исход, предсказуемые. 3) Какие события называются неоднозначными? Как вы это понимаете? Приведите примеры. Неоднозначными называются события, которые имеют такой исход, который может произойти, т.е. похоже на определение случайного события. 3. Мотивация В науке и практике часто встречаются задачи, решая которые приходится составлять различные комбинации из конечного числа элементов и вычислять результат, т. е. решать комбинаторные задачи. Давайте вспомним героев басни Ивана Андреевича Крылова. А теперь переходим к изучению нового материала. Вспомним, как было у И.А. Крылова в басне «Квартет»: Проказница мартышка, Осёл, Козёл Да косолапый мишка Затеяли играть квартет… Помните, у Крылова? Начали музыканты играть – не получается. "Стой, братцы, стой! - кричит Мартышка. -Погодите! Как музыке идти? Ведь вы не так сидите». И так и эдак пересаживались – опять музыка на лад не идёт. Тут пуще прежнего пошли у них разборы. И споры, Кому и как сидеть…
|
Включаются в деловой ритм урока.
Вывод: однозначные и неоднозначные события отличаются исходом – у однозначных событий он определён, а у неоднозначных – нет. Это поможет нам при изучении новой темы.
Вероятно, крыловские музыканты так и не перепробовали всех возможных способов перемены мест. Однако, способов (исходов, возможностей) этих не так уж и много. Сегодня на уроке, используя математические знания, посчитаем, сколькими различными способами можно рассадить (пересадить, поменять местами, переставить) четверых музыкантов на четыре различных места. Открываем тетради, записываем тему урока. |
| 2. Изучение нового материала Сегодня мы рассмотрим с вами простейшие комбинации, которые можно составить из элементов конечного множества. И этими комбинациями являются перестановки. Запишите в своих тетрадях тему сегодняшнего урока: «Перестановки». Рассмотрим с вами следующую задачу (условия задачи записывайте в тетрадях). Задача 1. (начнем с 2 элементов)
Представим себе множество, состоящее из 2-х элементов.  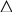  Это геометрические фигуры: и Это геометрические фигуры: и
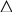 Сколькими способами можно их расположить? - Двумя (сначала , потом и наоборот). Сколькими способами можно их расположить? - Двумя (сначала , потом и наоборот).
Множество из 2-х элементов можно расположить упорядоченно 2-мя способами. Задача 2. (продолжим 3 элементами) Сколькими способами можно расставить на библиотечном стенде три журнала: по физике, по математике и по информатике? Давайте рассмотрим все возможные случаи таких расстановок. Пусть первым будет стоять журнал по физике (Ф). Тогда возможны такие расположения журналов: ФМИ, ФИМ. Если первым поставить журнал по математике (М), то можно получить следующие расположения: МФИ, МИФ. А если первым поставить журнал по информатике (И), то можно получить следующие расположения: ИФМ, ИМФ. Таким образом, мы можем расставить на стенде три журнала 6 способами.
Каждое из полученных нами расположение (МИФ, ИМФ и др.) называют перестановкой из трех элементов. Давайте запишем общее определение перестановки из n элементов (запись справа). Число перестановок из n элементов обозначается Pn (и читается «P из n»).
Число перестановок из n элементов можно посчитать, не выписывая все комбинации элементов. Для этого достаточно воспользоваться комбинаторным правилом умножения. Сколькими способами можно выбрать первый элемент перестановки из n элементов? А сколькими способами можно выбрать второй элемент из оставшихся (n-1) элементов? И т. д. Тогда, по комбинаторному правилу умножения, получаем: Pn = n*(n-1)*…*2*1. Если мы расположим множители в порядке возрастания, то получим Pn=1*2*3*…*(n-2)*(n-1)*n. Запишите это. Можно заметить, что мы записали произведение первых n натуральных чисел. Для обозначения такого произведения используют запись «n!» (читается «n факториал»). Таким образом, число всевозможных перестановок из n элементов вычисляется по формуле Pn=n!. Запишите это. Например, 2! = 1*2 = 2; 5! = 1*2*3*4*5 = 120. Запишите эти примеры себе в тетради. Также отметьте, что по определению, 0! = 1.
Таким образом, возвращаясь к задаче о расстановке журналов, количество способов можно было посчитать по формуле P(3) = 1*2*3 = 6. Отметьте это как второй способ решения. |
(Записывают тему урока) (Записывают условие и решение) Задача 1. Сколькими способами можно расставить на библиотечном стенде три журнала: по физике, по математике и по информатике? Решение. Возможные расстановки. Если первым стоит журнал по физике (Ф): ФМИ, ФИМ. Если первым стоит журнал по математике (М): МФИ, МИФ. Если первым стоит журнал по информатике (И): ИФМ, ИМФ. N = 6 способов. Ответ: 6 способов.
Перестановкой из n элементов называется каждое расположение этих элементов в определенном порядке. Работа с учебником ( стр 187) Число перестановок из n элементов обозначается Pn («P из n»).
N способами.
(N-1) способами.
Pn=1*2*3*…*(n-2)*(n-1)*n
Число всевозможных перестановок из n элементов: Pn=n!.
2! = 1*2 = 2; 5! = 1*2*3*4*5 = 120.
По определению, 0! = 1.
2 способ решения задачи 1. P(3) = 1*2*3 = 6 (способов). Ответ: 6 способов. |
| 3. Закрепление изученного материала
Теперь перейдем к решению задачи из басни. Возьмём множество из 4-х элементов А, Б, В и Г. Рассмотрим предыдущие перестановки А, Б, В В А Б А В Б А Б В Рассмотрим только первую строчку В А Б. Букву Г можно подставить перед буквами В, А, Б или после Б. Г В А Б В Г А Б В А Г Б В А Б Г Т. е. из одной строчки – получается четыре, в 4 раза больше. И так для каждой строки. Вывод: значит, число перестановок из 4-х элементов или Р4 равно 24, т. е. в 4 раза больше, чем Р3. Р4=Р3×4=1×2×3×4=24 сколькими различными способами можно рассадить (пересадить, поменять местами, переставить) четверых музыкантов на четыре различных места? Следовательно, P4=24 – число перестановок из 4-х элементов. Значит, крыловских музыкантов можно расположить 24 различными способами.
Р1=1!=1
№ 732 Сколькими способами 4 человека могут разместиться на четырехместной скамейке?
№ 734 (самостоятельно с последующей проверкой) Сколькими способами 9 человек могут встать в очередь в театральную кассу?
№ 737 (а) Сколько шестизначных чисел, в записи которых каждая цифра используется только один раз, можно составить из цифр 1, 2, 5, 6, 7, 8?
№ 738 (б) Сколько среди четырехзначных чисел, составленных из цифр 3, 5, 7, 9 (без их повторения), таких, которые кратны 15?
№ 739 Найдите сумму цифр всех четырехзначных чисел, которые можно составить из цифр 1, 3, 5, 7 (без их повторения). |
(Оформляют решение задач в тетради; у доски при решении примеров также работают учащиеся).
№ 732 P(4) = 1*2*3*4 = 24 (способа). Ответ: 24 способа.
№ 734 P(9) = 1*2*3*4*5*6*7*8*9 = 362880 (способов). Ответ: 362880 способами.
№ 737 P(6) = 1*2*3*4*5*6 = 720 (чисел). Ответ: 720 чисел.
№ 738 Т.к. сумма 3+5+7+9=24 кратна 3, то для того, чтобы составленное из этих цифр число было кратно 15, необходимо, чтобы оно заканчивалось на 5. Тогда N=P(3)*1=1*2*3*1=6 (чисел). Ответ: 6 чисел.
№ 739 Кол-во четырехзначных чисел, которые можно составить из цифр 1, 3, 5, 7: P(4) = 1*2*3*4 = 24 (числа). Т.к. числа состоят из одинаковых цифр, то сумма всех цифр полученных чисел будет равна 24*(1+3+5+7)=384. Ответ: 384. |
| 4. Подведение итогов Подведем итоги нашего занятия. С каким понятие комбинаторики вы познакомились сегодня на уроке? Что называется перестановкой из n элементов?
По какой формуле подсчитывается число всевозможных перестановок из n элементов? |
(Отвечают на вопросы) С понятием «Перестановки из n элементов». Перестановкой из n элементов называется каждое расположение этих элементов в определенном порядке. Число всевозможных перестановок из n элементов рассчитывается по формуле Pn=n!. |
| 5. Домашнее задание п. 31. № 733, № 735, № 736, № 737 (б), № 738 (а) |
Прокомментировать |
Резерв
Группа 1. Задание:
Тренер волейбольной команды решил изменить расположение игроков:
- Следующую встречу мы будем начинать по-другому, - объявил он после очередного проигрыша.
- А если опять проиграем?
- Тогда буду опять менять местами, пока не перепробую все возможные расположения, - ответил тренер.
Как известно, у волейболистов в команде 6 игроков.
Вопрос задачи:
-
как подсчитать, сколькими способами можно переставить 6-х волейболистов на 6 различных мест?
-
сколько потребуется времени, если каждый месяц пробовать 10 различных способов.
Решение: чтобы ответить на первый вопрос, надо подсчитать число перестановок из 6 элементов.
Р6=6!=120×6=720, т.е. существует 720 способов расставить спортсменов.
Чтобы ответить на второй вопрос задачи:
1). 720:10=72(мес.)
2).72:12=6 (лет)
Ответ: 6 лет.
Группа 2. Задание:
В расписании на вторник шесть уроков: русский язык, математика, история, литература, ОБЖ, биология.
Сколькими способами можно составить расписание уроков на этот день так, чтобы русский язык и литература стояли рядом для написания сочинения?
Решение: чтобы ответить вопрос, надо рассматривать русский язык и литературу как один предмет, поэтому необходимо найти число перестановок из 5-и элементов (120), однако, в каждой из получившихся комбинаций русский язык и литературу можно менять местами, т. е. находим число перестановок из двух элементов (2). Значит, искомое число способов Р5× Р2.
Р5× Р2=5! ×2!=120×2=240, т.е. существует 240 различных способов расставить уроки.
Ответ: 240 способов.
Группа 3. Задание:
Водитель покинул место ДТП. Очевидцы заметили, что в номере автомобиля присутствовали цифры 2, 4, 6 и буквы м, о, к. Цвет в период полярной ночи рассмотреть не удалось, а номер региона был известен. Сколько автомобилей предстоит проверить инспекторам ГИБДД?
Решение: чтобы ответить на вопрос, надо рассматривать отдельно комбинацию из 3-х различных цифр и комбинацию из 3-х различных букв. Сначала необходимо найти число перестановок из 3 элементов (6) для трёх известных цифр, однако, в каждой из получившихся комбинаций три буквы можно менять местами, т. е. находим число перестановок из 3-х элементов (6). Значит, искомое число способов Р3× Р3.
Р3×Р3=3!×3!=6×6=36, т.е. существует 36 различных номеров автомобилей, которые необходимо проверить инспектору ГИБДД.
Ответ: 36 способов.
| Сколько различных четырехзначных чисел, в которых цифры не повторяются, можно составить из цифр 0, 1, 3, 5? | Из цифр 0, 1, 3, 5 получится P4 перестановок – число перестановок из 4-х элементов. Однако, надо исключить те перестановки, которые начинаются с 0, т. к. число начинать 0 не может. Число таких перестановок P3. Значит, искомое количество четырехзначных чисел равно P4 - P3. Решение: P4 - P3= 4! – 3!= 24-6=18. |