Министерство образования, науки и молодежи Республики Крым
Государственное бюджетное профессиональное образовательное
учреждение Республики Крым
"Симферопольский автотранспортный техникум"
Методическая разработка открытого занятия
по дисциплине: ЕН.01 Математика
тема: «Перестановки, размещения и сочетания»
Разработчик: Пронина Е.А., преподаватель математики

Симферополь
2020
Тема занятия: “Перестановки, размещения и сочетания”
Цели занятия.
Дидактические:
- создание условий для применения знаний и умений в знакомой и новых учебных ситуациях.
Образовательные:
- обеспечить усвоение обучающимися формул комбинаторики;
- научить выделять существенные признаки формул.
Развивающие:
- развитие инициативы, уверенности в своих силах;
- развитие аналитического мышления.
Воспитательные:
- воспитание положительного отношения к знаниям;
- воспитание дисциплинированности.
Методические:
- апробация информационного метода с элементами проблемной ситуации, приема ученического целеполагания, индивидуальной работы с обучающимися.
Формируемые личностные результаты:
- выбор способов решения задач профессиональной деятельности, применительно к различным контекстам.
- использование информационных технологий в профессиональной деятельности;
- проявление доброжелательности к окружающим, деликатности, чувства такта и готовности оказать услугу каждому, кто в ней нуждается.
Тип занятия: урок комплексного применения знаний.
Вид занятия: практическая работа.
Технологии: проблемная, информационная
Межпредметные связи: электротехника, химия, экономика, статистика.
Обеспечение занятия: презентация, мультимедиа, дидактический материал.
Литература:
1. И.Д. Пехлецкий «Математика», 2001.
2. А.Е. Рудник «Сборник задач», 1974.
3. Н.В. Богомолов «Практикум по математике», 2000.
4. В.Н. Матвеев «Курс математики для техникума», 1976.
5. Е.В. Филимонова «Математика», 2005.
Структура занятия.
1. Организационный момент (5 мин).
2. Целеполагание и мотивация (10 мин).
3. Актуализация знаний (20 мин).
4. Применение знаний (упражнения) (45 мин).
- в знакомой ситуации (типовые)
- в новой ситуации (проблемные)
5. Информация о домашнем задании (5 мин).
6. Рефлексия (подведение итогов) (5 мин).
ХОД ЗАНЯТИЯ
| № | Этапы урока | Содержание этапов | Методы и приемы обучения | Деятельность |
| преподавателя | обучающихся |
| 1. | Организационный момент | 1. Отметка отсутствующих 2. Раздача тетрадей | Информационный | Отмечает по журналу | Староста (дежурный) информирует |
| 2. | Целеполагание и мотивация | Сообщение темы, целей, плана урока | Метод ученического целеполагания | Помогает сформулировать цели занятия | Ставят цели занятия |
| 3. | Актуализация знаний | Решение проблемных задач
| Информационный с элементами проблемной ситуации | Ставит проблему | Разрешают, записывают |
| 4. | Применение знаний (упражнения) |
| - в знакомой ситуации (типовые) | 1. Понятие 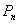
Вывод 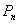 2. Закрепление в ходе решения. 3. Понятие 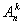 4. Закрепление в ходе решения 5.Понятие  6. Закрепление в ходе решения | Монологический, диалогический | Изложение материала в форме беседы с последующими записями в тетрадь, решение примеров | Вступают в беседу, составляют конспект |
| - в новой ситуации (проблемные) | Решение уравнений и задач | Проблемный. Общий контроль, индивидуальная работа с обучающимися | Решает примеры. Ставит проблему. Выдает задание. | Решают в тетрадях и на доске, элементы самостоятельной работы. |
| 5. | Информация о домашнем задании | Выдача домашнего задания | Монологический с элементами диалога | Словесная | Словесная, записывают в конспект |
| 6 | Рефлексия (подведение итогов) | 1. Подведение итогов 2. Оценка работоспособности | Монологический с элементами диалога | Словесная | Словесная |

Содержание практической работы
-
Теоретический этап.
Составление опорного конспекта.
Рассмотрим k множеств М , М
, М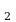 , М
, М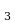 , …, М
, …, М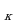 , содержащих по m
, содержащих по m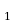 , m
, m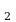 , m
, m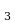 ,…, m
,…, m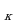 элементов соответственно. Выбирается по одному элементу из каждого множества и составляется еще одно множество. Число способов, которыми можно выбрать по одному элементу из каждого множества, равно произведению m
элементов соответственно. Выбирается по одному элементу из каждого множества и составляется еще одно множество. Число способов, которыми можно выбрать по одному элементу из каждого множества, равно произведению m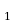 ∙ m
∙ m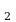 ∙ m
∙ m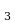 ∙…∙ m
∙…∙ m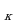 . В этом и состоит основной принцип произведения комбинаторики.
. В этом и состоит основной принцип произведения комбинаторики.
В задачах теории вероятностей часто рассматриваются различные соединения (комбинации) k элементов из множества, содержащего n элементов (k≤n). Будем рассматривать такие соединения, в которые каждый элемент данного множества может входить не более одного раза, то есть соединения без повторений. Рассмотрим три вида соединений: размещения, перестановки, сочетания.
Размещениями из n элементов по k элементов называются наборы k элементов, отличающиеся один от другого или самими элементами (составом элементов), или их порядком. Число размещений обозначается 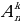 .
.
Число размещений из n элементов по k элементов находится по формуле:
А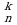 =n∙(n–1)∙(n–2)∙…∙(n–(k–1)) (1)
=n∙(n–1)∙(n–2)∙…∙(n–(k–1)) (1)
Перестановками из данных n элементов называются наборы из n элементов, различающихся только порядком.
Перестановки – это частный случай размещений. Число всех перестановок обозначают символом Р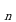 . Число Р
. Число Р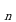 найти несложно. Для этого в формулу (1) подставляем k=n.
найти несложно. Для этого в формулу (1) подставляем k=n.
Р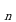 =n∙(n–1)∙(n–2)∙…∙(n–(k–1))∙…∙2∙1=n!
=n∙(n–1)∙(n–2)∙…∙(n–(k–1))∙…∙2∙1=n!
Произведение n первых натуральных чисел называется факториалом числа n и обозначается символом n! (читается «эн факториал»).
Р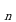 =1·2·3 …∙n=n! (2)
=1·2·3 …∙n=n! (2)
Приведем некоторые значения факториала:
0!=1, 5!= 1·2·3·4∙5=120,
1!=1, 6!= 1·2·3·4∙5∙6=720,
2!=1·2=2, 7!= 1·2·3·4∙5∙6∙7=5040,
3!=1·2·3=6, 8!= 1·2·3·4∙5∙6∙7∙8=40320,
4!=1·2·3·4=24, 9!= 1·2·3·4∙5∙6∙7∙8∙9=362880.
Сочетаниями, содержащими k элементов, выбранных из n элементов заданного множества, называются всевозможные наборы k элементов, различающиеся хотя бы одним элементом. Число сочетаний из n элементов по k элементам обозначают 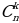 .
.
Число сочетаний из n элементов по k элементам определяется формулой:
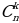 =
= 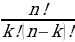 (3)
(3)
Пример 1. Определить, сколько трехзначных чисел можно составить из множества цифр 7,8,9,3,2 без повторений.
Решение. Трехзначные числа можно рассматривать как размещения, так как при замене одной цифры другой или перестановке их местами получаются разные числа. Так как n=5, k=3, то различных чисел будет:
А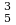 =5·4·3=60.
=5·4·3=60.
Пример 2. К кассе за получением (или для уплаты) денег подошли одновременно 4 человека. Сколькими способами они могут выстроиться в очередь?
Решение. Очередь состоит из 4 различных лиц, поэтому в каждом способе составления очереди учитывается порядок их расположения. Таким образом, имеют место перестановки из четырёх человек, их число равно:
Р4 = 4! = 24.
Пример 3. В цехе 18 человек, из них 10 мужчин. На конференцию отбирают 6 человек так, что было 3 мужчины и 3 женщины. Сколько различных списков можно составить?
Решение. 3-х мужчин из 10 человек можно отобрать С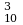 различными способами, 3-х женщин из 8 можно отобрать С
различными способами, 3-х женщин из 8 можно отобрать С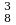 различными способами. Следовательно, 3-х женщин и 3-х мужчин можно отобрать С
различными способами. Следовательно, 3-х женщин и 3-х мужчин можно отобрать С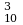 · С
· С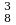 – различными способами.
– различными способами.
Найдем: С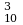 =
= =
=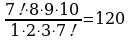 ,
,
С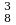 =
=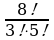 =
=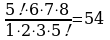 .
.
Итого, число различных списков: С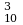 ∙ С
∙ С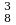 = 120 · 54 = 6480.
= 120 · 54 = 6480.
-
Подготовительный этап.
Перепишите и заполните пропуски:
Пример 1. За столом пять мест. Сколькими способами можно расставить пятерых гостей?
Решение. Р5 = 5! = 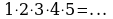 способов
способов
Ответ: 120 способов.
Пример 2.
а) Сколько трехзначных чисел можно записать, используя цифры 1,3,6,7,9, если каждая из них может быть использована в записи только один раз?
Решение. Искомое число вариантов равно числу размещений из 5 элементов по 3 элемента, т.е. по формуле получаем: 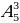 = 5
= 5  4
4  3 = … чисел.
3 = … чисел.
Ответ: 60 чисел.
б) Из 20 студентов надо выбрать старосту, его заместителя и редактора газеты. Сколькими способами это можно сделать?
Решение. Искомое число вариантов равно числу размещений из 20 элементов по 3 элемента, т.е. по формуле получаем: 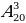 = 20
= 20  19
19  18 = … способов.
18 = … способов.
Ответ: 6840 способов.
Пример 3.
а) Из 15 членов туристической группы надо выбрать трех дежурных. Сколькими способами можно сделать этот выбор?
Решение. Каждый выбор отличается от другого хотя бы одним дежурным. Значит, здесь речь идет о сочетаниях из 15 элементов по 3. Следовательно, по формуле получаем 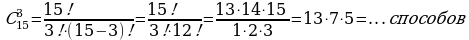
Ответ: 455 способов.
б) Студентам дали список из 10 книг, которые рекомендуется прочитать во время каникул. Сколькими способами студент может выбрать из них 6 книг?
Решение. Выбор 6 из 10 без учёта порядка: 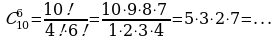 способов.
способов.
Ответ: 210 способов.
-
Практический этап.
Задание 1. Вычислить:
а) 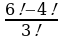 ; б)
; б) 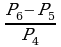 ; в)
; в) 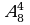 ;
; 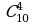 .
.
Задание 2. Упростить: 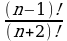 .
.
Задание 3. Сколькими способами можно составить список из 8 обучающихся, если у них различные инициалы?
Задание 4. Сколько существует вариантов трехзначного цифрового кода?
Задание 5. На факультете изучается 16 предметов. На понедельник в расписание нужно поставить 3 предмета. Сколькими способами это можно сделать?
Задание 6. На родительском собрании присутствует 20 человек. Сколько существует различных вариантов состава родительского комитета, если в него должны войти 5 человек?
Дополнительные задания*.
Вариант 1
1. Вычислить: 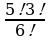 .
.
2. Упростить: 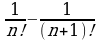 .
.
3. Вычислить: 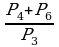 .
.
4. Вычислить: 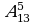 ;
; 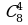 .
.
Вариант 2
1. Вычислить: 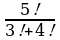 .
.
2. Упростить: 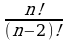 .
.
3. Вычислить: 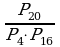 .
.
4. Вычислить: 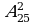 ;
; 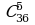 .
.









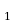 , М
, М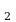 , М
, М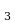 , …, М
, …, М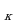 , содержащих по m
, содержащих по m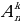 .
.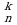 =n∙(n–1)∙(n–2)∙…∙(n–(k–1)) (1)
=n∙(n–1)∙(n–2)∙…∙(n–(k–1)) (1)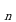 . Число Р
. Число Р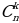 .
.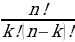 (3)
(3)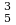 =5·4·3=60.
=5·4·3=60.
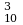 различными способами, 3-х женщин из 8 можно отобрать С
различными способами, 3-х женщин из 8 можно отобрать С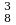 различными способами. Следовательно, 3-х женщин и 3-х мужчин можно отобрать С
различными способами. Следовательно, 3-х женщин и 3-х мужчин можно отобрать С =
=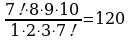 ,
, 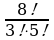 =
=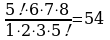 .
.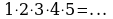 способов
способов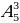 = 5
= 5  4
4 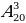 = 20
= 20 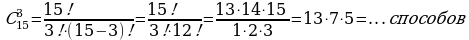
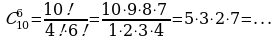 способов.
способов.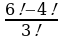 ; б)
; б) 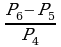 ; в)
; в) 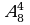 ;
; 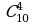 .
.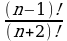 .
.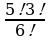 .
.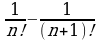 .
.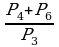 .
.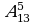 ;
; 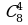 .
.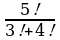 .
.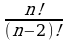 .
.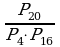 .
.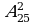 ;
; 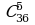 .
.

















