Перпендикуляр и наклонные

ПЕРПЕНДИКУЛЯР И НАКЛОННАЯ

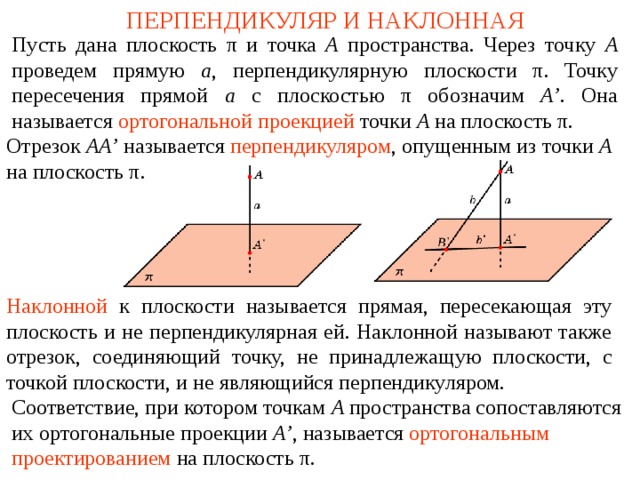
Пусть дана плоскость π и точка A пространства. Через точку A проведем прямую a , перпендикулярную плоскости π . Точку пересечения прямой a с плоскостью π обозначим A’ . Она называется ортогональной проекцией точки A на плоскость π .

Отрезок AA’ называется перпендикуляром , опущенным из точки A на плоскость π .

Наклонной к плоскости называется прямая, пересекающая эту плоскость и не перпендикулярная ей. Наклонной называют также отрезок, соединяющий точку, не принадлежащую плоскости, с точкой плоскости, и не являющийся перпендикуляром.

В режиме слайдов ответ появляется после кликанья мышкой.

Соответствие, при котором точкам A пространства сопоставляются их ортогональные проекции A’ , называется ортогональным проектированием на плоскость π .

Теорема о трех перпендикулярах

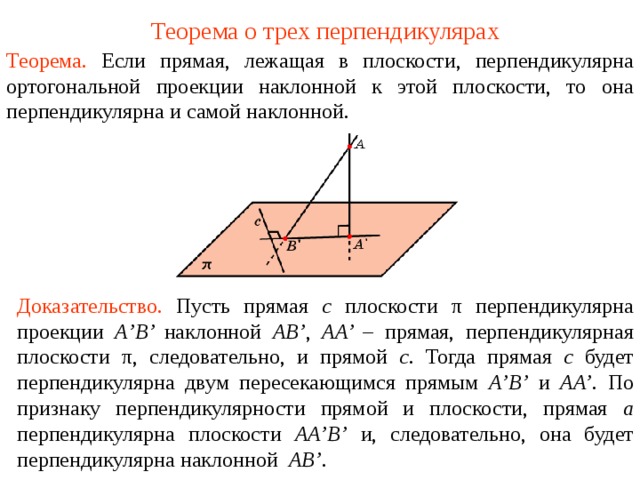
Теорема. Если прямая, лежащая в плоскости, перпендикулярна ортогональной проекции наклонной к этой плоскости, то она перпендикулярна и самой наклонной.

Доказательство. Пусть прямая c плоскости π перпендикулярна проекции A ’B’ наклонной AB’ , AA’ – прямая, перпендикулярная плоскости π , следовательно, и прямой c . Тогда прямая c будет перпендикулярна двум пересекающимся прямым A’B’ и AA’ . По признаку перпендикулярности прямой и плоскости, прямая а перпендикулярна плоскости А A’ В ’ и, следовательно, она будет перпендикулярна наклонной АВ ’ .

В режиме слайдов ответ появляется после кликанья мышкой.

Упражнение 1

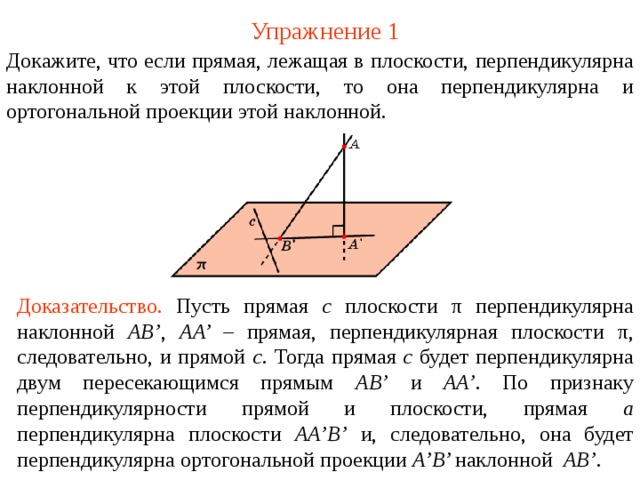
Докажите, что е сли прямая, лежащая в плоскости, перпендикулярна наклонной к этой плоскости, то она перпендикулярна и ортогональной проекции этой наклонной.

Доказательство. Пусть прямая c плоскости π перпендикулярна наклонной AB’ , AA’ – прямая, перпендикулярная плоскости π , следовательно, и прямой c . Тогда прямая c будет перпендикулярна двум пересекающимся прямым AB’ и AA’ . По признаку перпендикулярности прямой и плоскости, прямая а перпендикулярна плоскости А A’ В ’ и, следовательно, она будет перпендикулярна ортогональной проекции A’B’ наклонной АВ ’ .

В режиме слайдов ответ появляется после кликанья мышкой.

Упражнение 2

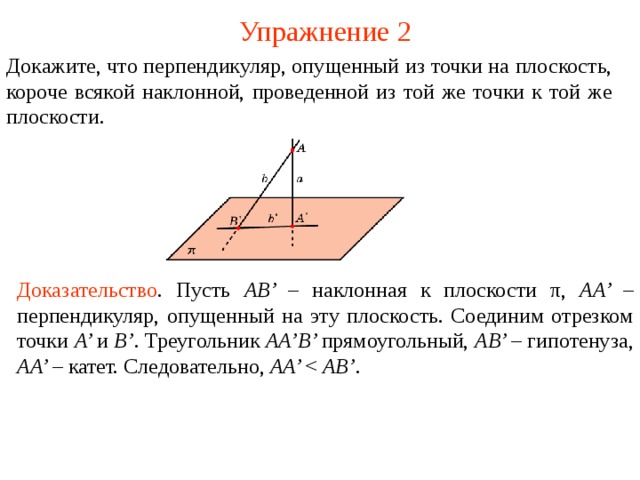
Докажите, что п ерпендикуляр, опущенный из точки на плоскость, короче всякой наклонной, проведенной из той же точки к той же плоскости.

Доказательство . Пусть AB’ – наклонная к плоскости π , AA’ – перпендикуляр, опущенный на эту плоскость. Соединим отрезком точки A’ и B’ . Треугольник AA’B’ прямоугольный, AB’ – гипотенуза, AA’ – катет. Следовательно, AA’ AB’ .

В режиме слайдов ответ появляется после кликанья мышкой.

Упражнение 3

Может ли ортогональная проекция отрезка быть: а) меньше отрезка; б) равна отрезку; в) больше отрезка?

В режиме слайдов ответ появляется после кликанья мышкой.

Ответ: а) Да;

б) д а;

в) нет.

Упражнение 4

Верно ли утверждение: «Если из двух различных точек, не принадлежащих плоскости, проведены к ней две равные наклонные, то их проекции тоже равны»?

В режиме слайдов ответ появляется после кликанья мышкой.

Ответ: Нет.

Упражнение 5

К плоскости прямоугольника ABCD в точке пересечения диагоналей восстановлен перпендикуляр. Верно ли утверждение о том, что произвольная точка M этого перпендикуляра равноудалена от вершин прямоугольника?

В режиме слайдов ответ появляется после кликанья мышкой.

Ответ: Да.

Упражнение 6

Точка M равноудалена от всех точек окружности. Верно ли утверждение о том, что она принадлежит перпендикуляру к плоскости окружности, проведённому через её центр?

В режиме слайдов ответ появляется после кликанья мышкой.

Ответ: Да.

Упражнение 7

Найдите ГМ оснований наклонных одинаковой длины, проведённых к данной плоскости из данной точки.

В режиме слайдов ответ появляется после кликанья мышкой.

Ответ: Окружность.

Упражнение 8

Найдите геометрическое место точек в пространстве, равноудаленных от двух данных точек.

В режиме слайдов ответ появляется после кликанья мышкой.

Ответ: Плоскость, проходящая через середину отрезка, соединяющего данные точки, и перпендикулярная этому отрезку.

Упражнение 9

Найдите геометрическое место точек в пространстве, равноудаленных от трех данных точек, не принадлежащих одной прямой.

В режиме слайдов ответ появляется после кликанья мышкой.

Ответ: Прямая, проходящая через центр описанной окружности треугольника с вершинами в данных точках, и перпендикулярная плоскости этого треугольника.

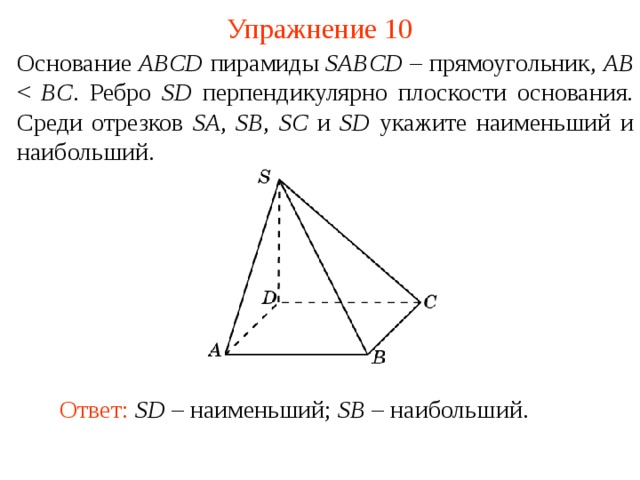
Упражнение 10

Основание ABCD пирамиды SABCD – прямоугольник, AB BC . Ребро SD перпендикулярно плоскости основания. Среди отрезков SA , SB , SC и SD укажите наименьший и наибольший.

В режиме слайдов ответ появляется после кликанья мышкой.

Ответ: SD – наименьший; SB – наибольший.

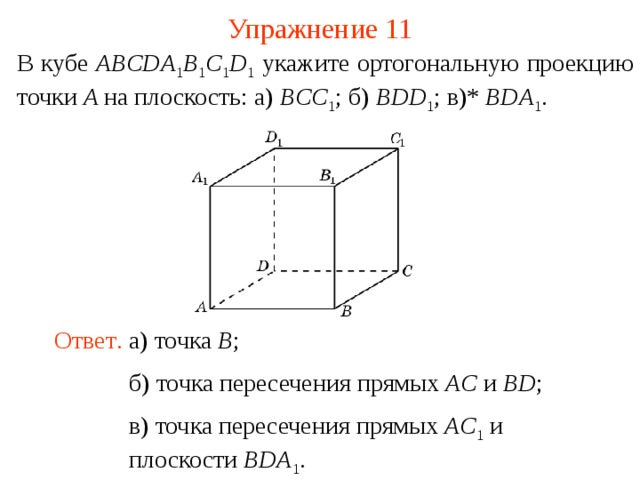
Упражнение 11

В кубе ABCDA 1 B 1 C 1 D 1 укажите ортогональную проекцию точки A на плоскость: а) BCC 1 ; б) BDD 1 ; в)* BDA 1 .

В режиме слайдов ответ появляется после кликанья мышкой.

Ответ . а) точка B ;

б) точка пересечения прямых AC и BD ;

в) точка пересечения прямых AC 1 и плоскости BDA 1 .

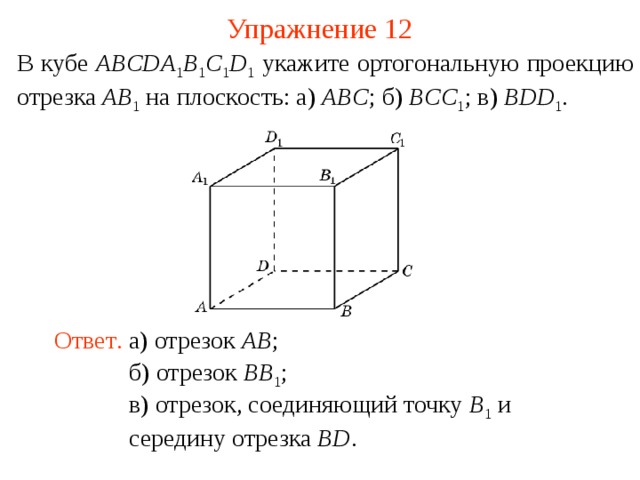
Упражнение 12

В кубе ABCDA 1 B 1 C 1 D 1 укажите ортогональную проекцию отрезка AB 1 на плоскость: а) ABC ; б) BCC 1 ; в) BDD 1 .

В режиме слайдов ответ появляется после кликанья мышкой.

Ответ . а) отрезок AB ;

б) отрезок BB 1 ;

в) отрезок, соединяющий точку B 1 и середину отрезка BD .

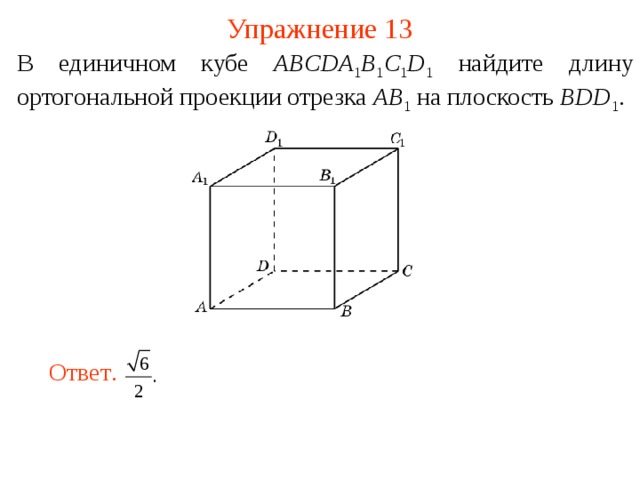
Упражнение 13

В единичном кубе ABCDA 1 B 1 C 1 D 1 найдите длину ортогональной проекции отрезка AB 1 на плоскость BDD 1 .

В режиме слайдов ответ появляется после кликанья мышкой.

Ответ .

15

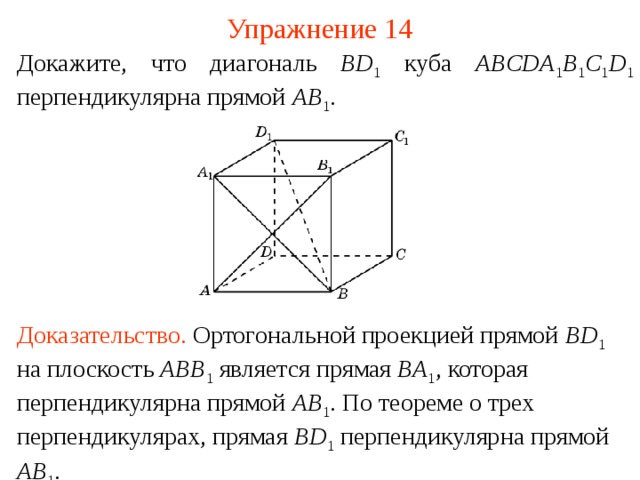
Упражнение 14

Докажите, что диагональ BD 1 куба ABCDA 1 B 1 C 1 D 1 перпендикулярна прямой AB 1 .

В режиме слайдов ответ появляется после кликанья мышкой.

Доказательство . Ортогональной проекцией прямой BD 1 на плоскость ABB 1 является прямая BA 1 , которая перпендикулярна прямой AB 1 . По теореме о трех перпендикулярах, прямая BD 1 перпендикулярна прямой AB 1 .

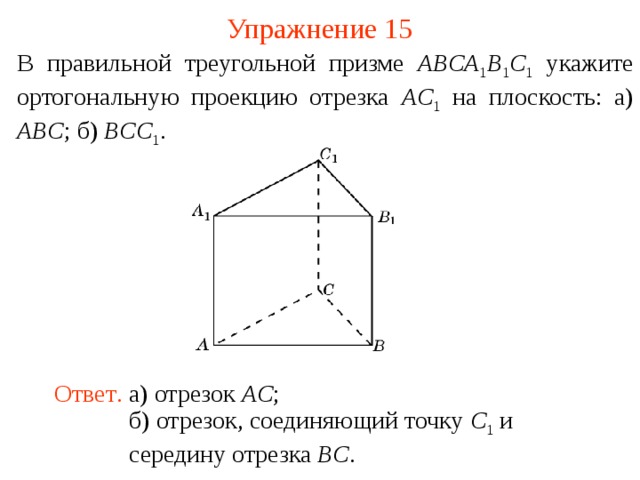
Упражнение 15

В правильной треугольной призме ABCA 1 B 1 C 1 укажите ортогональную проекцию отрезка AC 1 на плоскость: а) ABC ; б) BCC 1 .

В режиме слайдов ответ появляется после кликанья мышкой.

Ответ . а) отрезок AC ;

б) отрезок, соединяющий точку C 1 и середину отрезка BC .

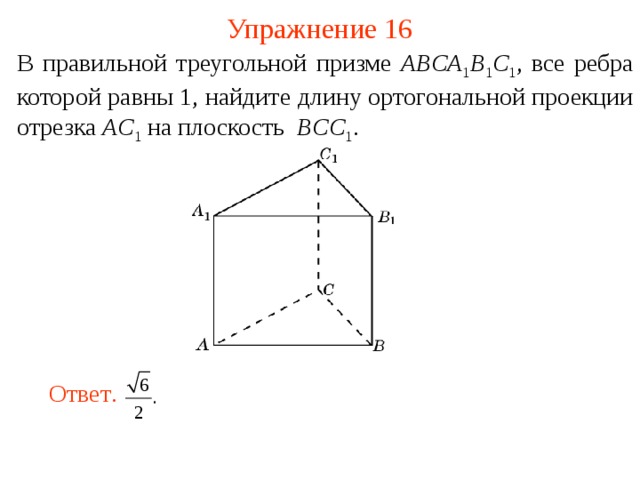
Упражнение 16

В правильной треугольной призме ABCA 1 B 1 C 1 , все ребра которой равны 1, найдите длину ортогональной проекции отрезка AC 1 на плоскость BCC 1 .

В режиме слайдов ответ появляется после кликанья мышкой.

Ответ .

18

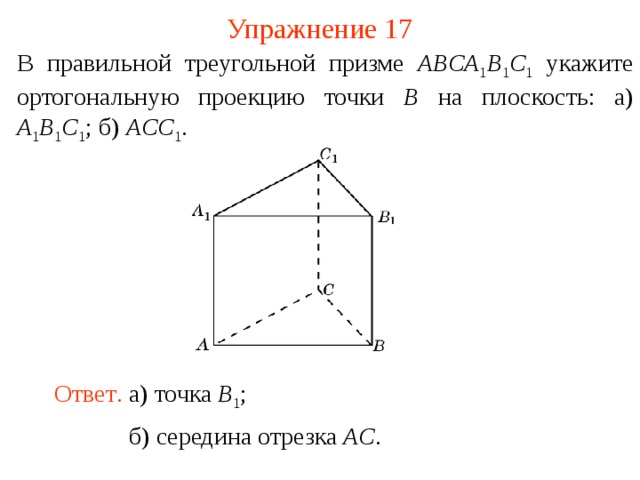
Упражнение 17

В правильной треугольной призме ABCA 1 B 1 C 1 укажите ортогональную проекцию точки B на плоскость: а) A 1 B 1 C 1 ; б) ACC 1 .

В режиме слайдов ответ появляется после кликанья мышкой.

Ответ . а) точка B 1 ;

б) середина отрезка AC .

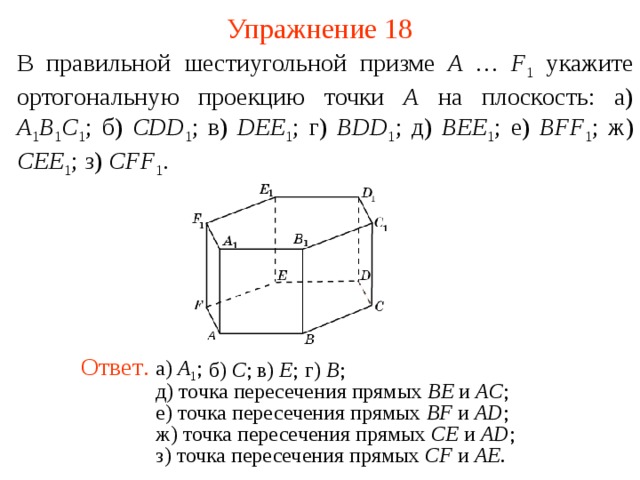
Упражнение 18

В правильной шестиугольной призме A … F 1 укажите ортогональную проекцию точки A на плоскость: а) A 1 B 1 C 1 ; б) CDD 1 ; в) DEE 1 ; г) BDD 1 ; д) BEE 1 ; е) BFF 1 ; ж ) CEE 1 ; з) CFF 1 .

В режиме слайдов ответ появляется после кликанья мышкой.

Ответ . а) A 1 ;

б) C ;

в) E ;

г) B ;

д) точка пересечения прямых BE и AC ;

е) точка пересечения прямых BF и AD ;

ж) точка пересечения прямых CE и AD ;

з) точка пересечения прямых CF и AE .

Упражнение 19

В правильной шестиугольной призме A … F 1 укажите ортогональную проекцию отрезка AC 1 на плоскость: а) ABC ; б) CDD 1 ; в) CEE 1 ; г) CFF 1 ; д) BEE 1 ; е) DFF 1 .

В режиме слайдов ответ появляется после кликанья мышкой.

Ответ . а) отрезок AC ;

б) отрезок C С 1 ;

в) отрезок, соединяющий точку C 1 и середину отрезка CE ;

г) отрезок, соединяющий точку C 1 и точку пересечения AF и AE ;

д) отрезок, соединяющий точку пересечения AC и BE с точкой пересечения A 1 C 1 и B 1 E 1 ;

е) отрезок FD 1 ;

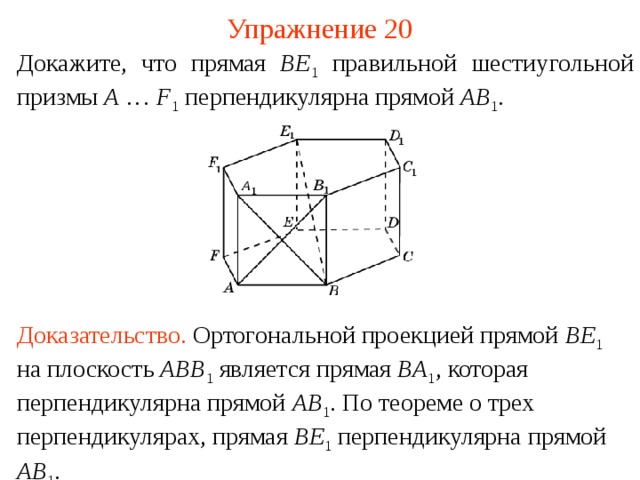
Упражнение 20

Докажите, что прямая BE 1 правильной шестиугольной призмы A … F 1 перпендикулярна прямой AB 1 .

В режиме слайдов ответ появляется после кликанья мышкой.

Доказательство . Ортогональной проекцией прямой BE 1 на плоскость ABB 1 является прямая BA 1 , которая перпендикулярна прямой AB 1 . По теореме о трех перпендикулярах, прямая BE 1 перпендикулярна прямой AB 1 .

Упражнение 21

Из точки A к данной плоскости проведены перпендикуляр и наклонная, пересекающие плоскость соответственно в точках B и C . Найдите проекцию отрезка AC , если AC = 37 см, AB = 35 см.

В режиме слайдов ответ появляется после кликанья мышкой.

Ответ: 12 см.

Упражнение 22

Из точки A к данной плоскости проведены перпендикуляр и наклонная, пересекающие плоскость соответственно в точках B и C . Найдите отрезок AC , если AB = 6 см,  BAC = 60°.

В режиме слайдов ответ появляется после кликанья мышкой.

Ответ: 12 см.

Упражнение 23

Из точки A к данной плоскости проведены перпендикуляр и наклонная, пересекающие плоскость соответственно в точках B и C . Найдите отрезок AB , если AC = см, BC = 3 AB .

В режиме слайдов ответ появляется после кликанья мышкой.

Ответ: 2 см.

Упражнение 24

Отрезки двух наклонных, проведенных из одной точки к плоскости, равны 15 см и 20 см. Проекция одного из этих отрезков равна 16 см. Найдите проекцию другого отрезка.

В режиме слайдов ответ появляется после кликанья мышкой.

Ответ: 9 см.

Упражнение 25

Отрезок BC длиной 12 см является проекцией отрезка AC на плоскость  . Точка D принадлежит отрезку AC и AD : DC = 2:3. Найдите отрезок AD и его проекцию на плоскость  , если известно, что AB = 9 см.

В режиме слайдов ответ появляется после кликанья мышкой.

Ответ: 6 см; 4,8 см.

Упражнение 26

Дан прямоугольный треугольник ABC , катеты которого AC и BC равны соответственно 20 и 15 см. Через вершину A проведена плоскость  , параллельная прямой BC . Проекция одного из катетов на эту плоскость равна 12 см. Найдите проекцию гипотенузы.

В режиме слайдов ответ появляется после кликанья мышкой.

Ответ: см.

Упражнение 27

Сторона ромба равна a , острый угол 60°. Через одну из сторон ромба проведена плоскость. Проекция другой стороны на эту плоскость равна b . Найдите проекции диагоналей ромба.

В режиме слайдов ответ появляется после кликанья мышкой.

Ответ: b и .