Теорема о трех перпендикулярах.

Перпендикуляр и наклонная.

Знать понятия:

Перпендикуляр к плоскости, его основание, наклонная к плоскости, ее основание, как найти проекцию наклонной, проведенной к плоскости.

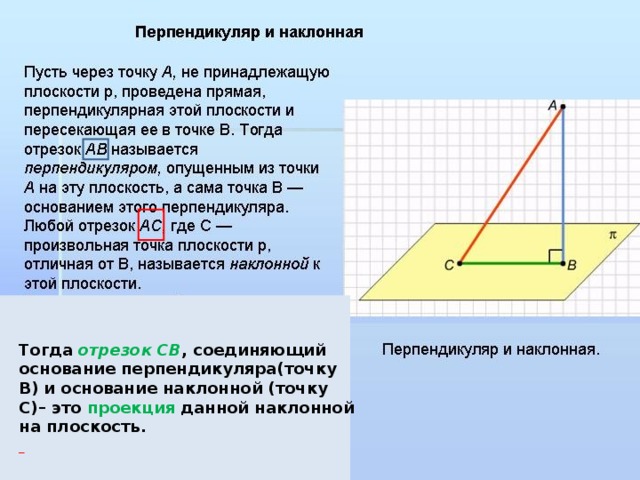
Тогда отрезок СВ , соединяющий основание перпендикуляра(точку В) и основание наклонной (точку С)– это проекция данной наклонной на плоскость.

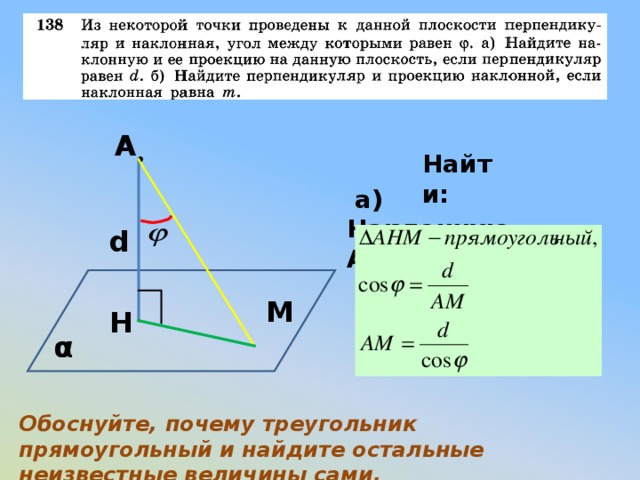
А

•

Найти:

а) Наклонную АМ

d

М

Н

α

Обоснуйте, почему треугольник прямоугольный и найдите остальные неизвестные величины сами.

Расстояние от точки до плоскости.

Знать понятия:

расстояние от точки до плоскости.

Обратите внимание как на рисунке обозначается расстояние ( величина «ро»)

плоскость.

Нетрудно догадаться, что расстоянием от точки до прямой будет длина перпендикуляра, проведенного из этой точки к данной прямой.

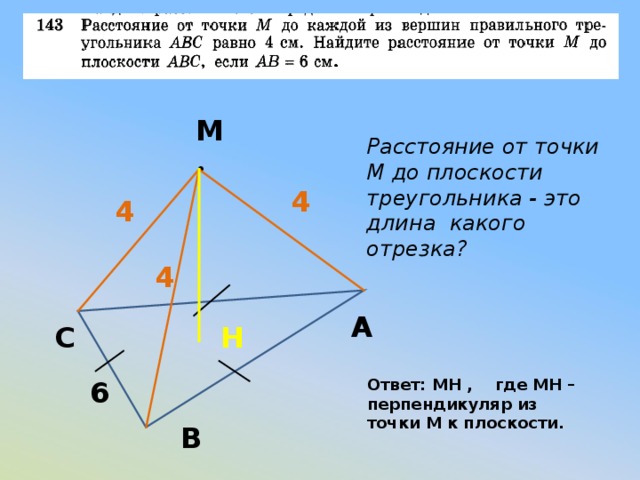
М

Расстояние от точки М до плоскости треугольника - это длина какого отрезка?

•

4

4

4

А

С

H

6

Ответ: MH , где MH – перпендикуляр из точки М к плоскости.

В

Как определить, где именно расположена внутри треугольника точка H?

М

•

4

4

Рассмотрите треугольники MHC, MHB, MHA. Докажите их равенство.

4

H

А

С

6

Сделайте вывод о равенстве отрезков HC, HB, HA.

В

Это значит, что точка Н равноудалена от вершин данного треугольника, т.е. она центр описанной около этого треугольника окружности. А т.к. этот треугольник правильный, то точка H – точка пересечения медиан(биссектрис, высот)

Найдите CH, зная сторону правильного треугольника, а затем из треугольника CHM найдите искомую высоту HM

Теорема о трех перпендикулярах.

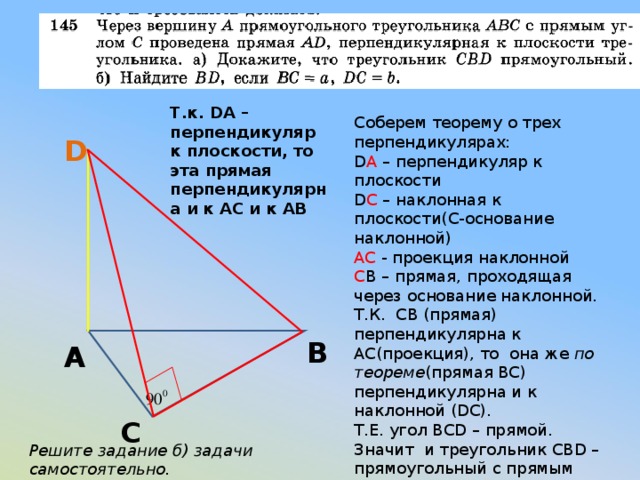
Т.к. DA – перпендикуляр к плоскости, то эта прямая перпендикулярна и к АС и к АВ

Соберем теорему о трех перпендикулярах:

D A – перпендикуляр к плоскости

D С – наклонная к плоскости(С-основание наклонной)

АС - проекция наклонной

С В – прямая, проходящая через основание наклонной.

Т.К. СВ (прямая) перпендикулярна к АС(проекция), то она же по теореме (прямая ВС) перпендикулярна и к наклонной (DC).

Т.Е. угол BCD – прямой. Значит и треугольник CBD – прямоугольный с прямым углом С.

D

В

А

С

Решите задание б) задачи самостоятельно.

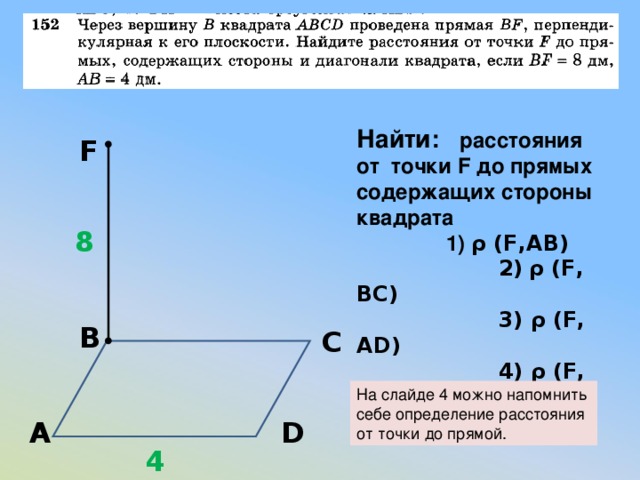
Найти: расстояния от точки F до прямых содержащих стороны квадрата

1) ρ (F,AB)

2) ρ (F, BC)

3) ρ (F, AD)

4) ρ (F, DC)

F

8

В

С

На слайде 4 можно напомнить себе определение расстояния от точки до прямой.

А

D

4

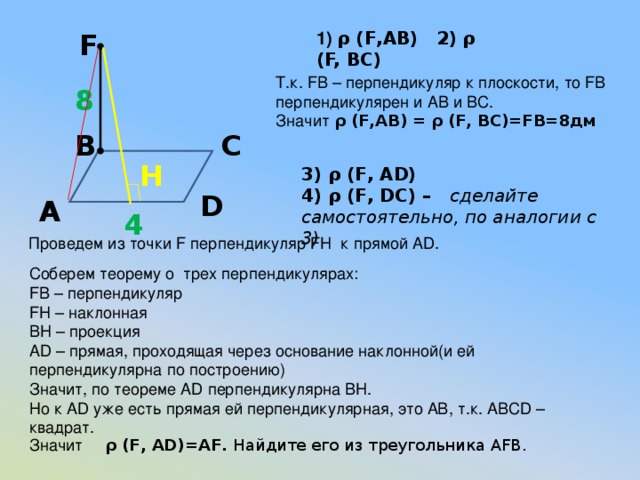
F

1) ρ (F,AB) 2) ρ (F, BC)

Т.к. FB – перпендикуляр к плоскости, то FB перпендикулярен и АВ и ВС.

Значит ρ (F,AB) = ρ (F, BC)=FB=8дм

8

С

В

H

3) ρ (F, AD)

4) ρ (F, DC) – сделайте самостоятельно, по аналогии с 3)

D

А

4

Проведем из точки F перпендикуляр FH к прямой AD.

Соберем теорему о трех перпендикулярах:

FB – перпендикуляр

FH – наклонная

BH – проекция

AD – прямая, проходящая через основание наклонной(и ей перпендикулярна по построению)

Значит, по теореме AD перпендикулярна BH.

Но к AD уже есть прямая ей перпендикулярная, это АВ, т.к. ABCD – квадрат.

Значит ρ (F, AD)=AF. Найдите его из треугольника AFB.

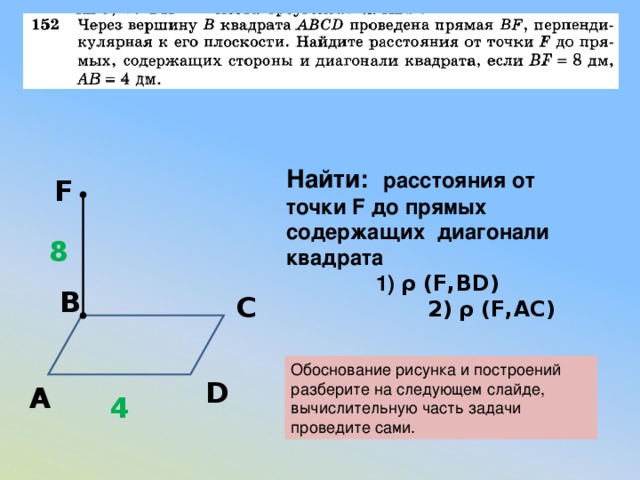
Найти: расстояния от точки F до прямых содержащих диагонали квадрата

1) ρ (F,BD)

2) ρ (F,AC)

F

8

В

С

Обоснование рисунка и построений разберите на следующем слайде, вычислительную часть задачи проведите сами.

D

А

4

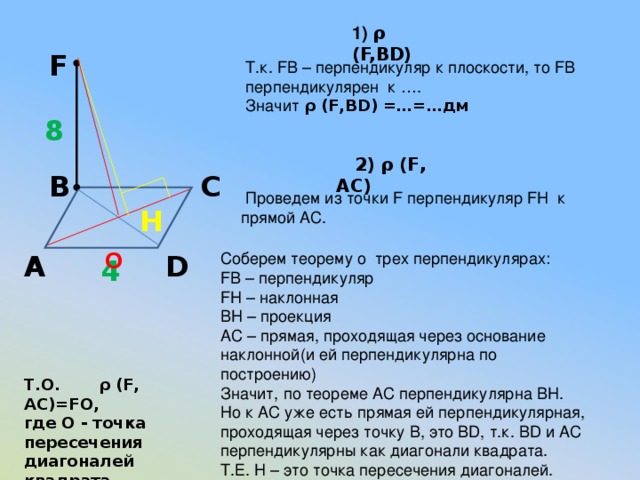
1) ρ (F,BD)

F

Т.к. FB – перпендикуляр к плоскости, то FB перпендикулярен к ….

Значит ρ (F,BD) =…=…дм

8

2) ρ (F, АC)

В

С

Проведем из точки F перпендикуляр FH к прямой AС.

H

О

Соберем теорему о трех перпендикулярах:

FB – перпендикуляр

FH – наклонная

BH – проекция

AС – прямая, проходящая через основание наклонной(и ей перпендикулярна по построению)

Значит, по теореме AС перпендикулярна BH.

Но к AС уже есть прямая ей перпендикулярная, проходящая через точку В, это ВD, т.к. BD и AC перпендикулярны как диагонали квадрата.

Т.Е. H – это точка пересечения диагоналей.

А

D

4

Т.О. ρ (F, АC)=FO,

где О - точка пересечения

диагоналей квадрата.