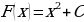Понятие первообразной.
Сегодня мы познакомимся с новым математическим понятием – первообразной. Что это такое?
Для начала обратимся к задаче, которая поможет сформулировать определение первообразной.
С точки зрения механики скорость прямолинейного движения определяется как производная пути по времени.
Если некоторая точка прошла путь 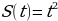 , то ее мгновенная скорость в любой момент времени может быть рассчитана по формуле
, то ее мгновенная скорость в любой момент времени может быть рассчитана по формуле 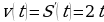 .
.
Если теперь рассмотреть обратную задачу – нахождение пути, пройденного точкой с заданной скоростью, то придем к функции S(t), которую называют первообразной функции v(t), т.е. такой функцией, что 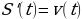 .
.
Задача №1. Известна производная функции у(х):

В этом примере мы выполнили операцию, обратную дифференцированию. В математическом анализе она называется интегрированием. Если интегрируют некоторую произвольную функцию f(х), то в итоге получают новую функцию, которую чаще всего обозначают как F(x). Её называют первообразной функции f(x).

Примеры первообразных:

Задача №2. Докажите, что функция 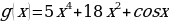 является первообразной для функции
является первообразной для функции 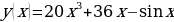 .
.
Проверим выполнение условия 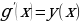 .
.
Бесконечное множество первообразных.
Рассмотрим функции и вычислим для них производные:
| 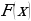
| 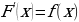
|
|
| 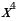
| 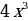
| |
| 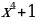
| 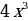
| |
| 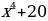
| 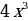
| |
| 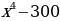
| 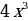
| |
| 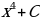
| 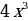
| Здесь C – некоторое число, т.е. параметр. |
Мы видим, что у всех функций из этого семейства, независимо от значения параметра С, производная одинакова. Здесь С может принимать любое действительное значение. Так как действительных чисел бесконечно много, то и количество функций, образующих семейство, также бесконечно. И все они являются первообразными для 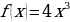 .
.
Мы доказали, что для любой функции есть бесконечное количество первообразных.
Данная особенность операции интегрирования может быть сформулирована в виде следующей теоремы:

Неопределенный интеграл
Каждая математическая операция имеет какое-то особое обозначение. Например, чтобы показать, что мы дифференцируем некоторую функцию, мы ставим после неё штрих (и при необходимости берем в скобки):
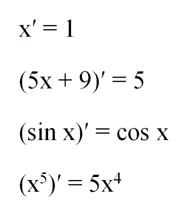
Напомним, что операция нахождения первообразной называется интегрированием. Для ее обозначения используется особый знак – интеграл. Например, мы знаем, что первообразная для 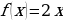 – это семейство функций вида
– это семейство функций вида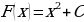
С помощью интеграла этот факт записывается так:

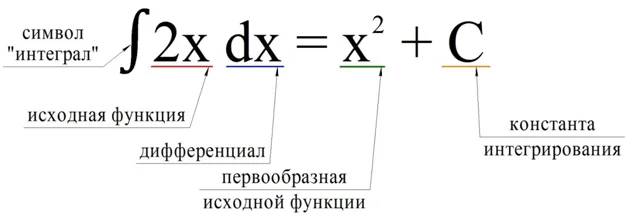
Исходная функция – это та самая функция, для которой необходимо найти первообразную, то есть интегрируемая функция. Справа от знака «равно» как раз записывается первообразная. Сразу после первообразной надо писать «+ С». Тем самым мы показываем, что у интегрируемой функции есть бесконечное количество первообразных.
После интегрируемой функции стоит так называемый дифференциал dх (читается как «дэ икс»). В данном случае он указывает, что именно буквой х мы обозначаем переменную в интегрируемой функции. Его значение мы разберем несколько позже. Пока что надо запомнить, что после интегрируемой функции необходимо писать «dx». В целом вся запись читается так: «интеграл от два икс по дэ икс равен икс в квадрате плюс цэ».
В чем разница между первообразной и интегралом?
Первообразная – это функция, при дифференцировании которой получается исходная функция. Интеграл же – это не функция, а целое семейство функций (или их множество), которое включает в себя сразу все первообразные интегрируемой функции.
Так как интегрирование – это действие, обратное дифференцированию, то мы можем проверить результат своих вычислений, выполнив обратную операцию.







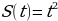 , то ее мгновенная скорость в любой момент времени может быть рассчитана по формуле
, то ее мгновенная скорость в любой момент времени может быть рассчитана по формуле 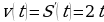 .
. 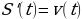 .
.


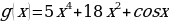 является первообразной для функции
является первообразной для функции 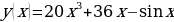 .
.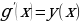 .
.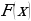
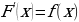
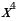
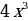
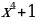
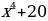
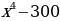
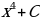
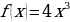 .
. 
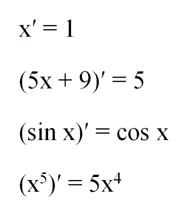
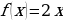 – это семейство функций вида
– это семейство функций вида