ПИРАМИДА.
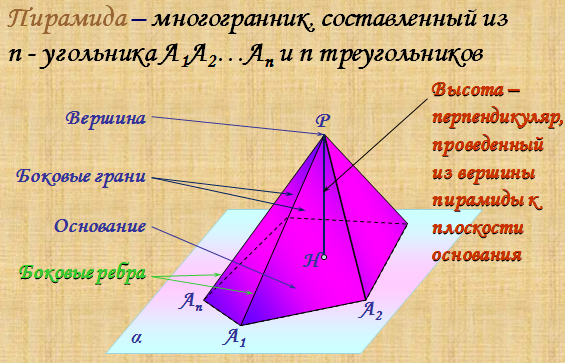
Пирамидой называется многогранник, который состоит из плоского многоугольника (основания пирамиды), точки, не лежащей в плоскости основания (вершины пирамиды), и всех отрезков, соединяющих вершину пирамиды с точками основания.

Рис. а) MABCD – пирамида, M – вершина пирамиды, MA, MB, MC, MD – боковые ребра
Пирамида называется n-угольной, если ее основанием является n-угольник.
Треугольная пирамида называется также тетраэдром.
Высотой пирамиды называется перпендикуляр, опущенный из вершины пирамиды на плоскость основания.
Отрезки, соединяющие вершину пирамиды с вершинами основания, называются боковыми ребрами
Основание пирамиды – грань пирамиды, являющаяся n-угольником.
Вершина пирамиды – общая точка всех треугольников, лежащих в боковых гранях, не принадлежащая плоскости основания
Боковая грань – грань пирамиды, являющаяся треугольником
Площадь боковой поверхности пирамиды – сумма площадей всех ее боковых граней. Обозначают Sбок
Площадь полной поверхности пирамиды – сумма площадей всех ее граней. Обозначают Sполн
Пирамида называется правильной, если ее основание – правильный многоугольник, а отрезок, соединяющий вершину пирамиды с центром основания, является ее высотой.
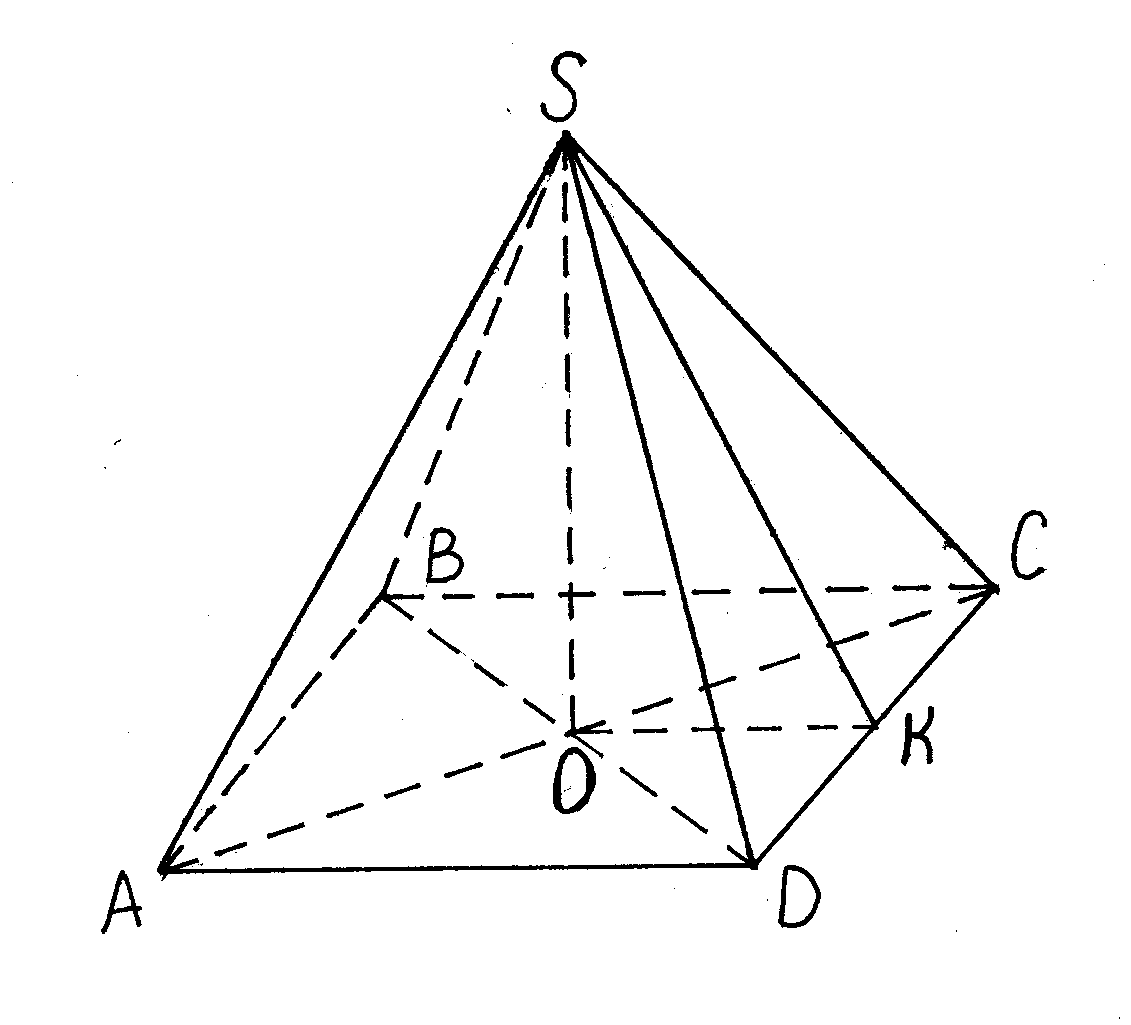
Все боковые ребра правильной пирамиды равны, а боковые грани являются равными равнобедренными треугольниками.
В правильной пирамиде:
1) все боковые ребра равны
2) все боковые ребра одинаково наклонены к плоскости основания
3) все боковые ребра образуют равные углы с высотой пирамиды
4) все боковые грани – равные равнобедренные треугольники.
Апофема – высота боковой грани правильной пирамиды, проведенная из ее вершины.
Все апофемы правильной пирамиды равны друг другу.
Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему.
УСЕЧЕННАЯ ПИРАМИДА
Если сечение пирамиды параллельно основанию, то мы получим усеченную пирамиду.
Усеченной пирамидой называется многогранник, который отсекается при пересечении пирамиды плоскостью, параллельной ее основанию.
Высота усеченной пирамиды – перпендикуляр, проведенный из любой точки одного основания к плоскости другого основания.
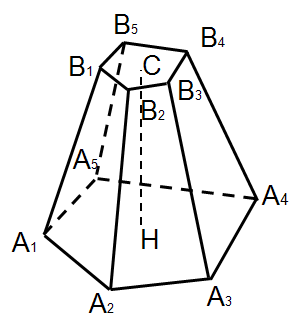
А1А2А3А4А5 и В1В2В3В4В5 - нижнее и верхнее основания усечённой пирамиды
А1В1, А2В2, А3В3… - боковые ребра усечённой пирамиды
А1В1В2А2, В2А2В3А3… - боковые грани усечённой пирамиды
СН – перпендикуляр, проведённый из какой-нибудь точки верхнего основания к нижнему основанию – называется высотой усечённой пирамиды
Свойства усеченной пирамиды:
-
Основания усеченной пирамиды — подобные многоугольники.
-
Боковые грани усеченной пирамиды — трапеции.
-
Боковые ребра правильной усеченной пирамиды равны и одинаково наклонены к основанию пирамиды.
-
Боковые грани правильной усеченной пирамиды — равные между собой равнобедренные трапеции и одинаково наклонены к основанию пирамиды.
-
Двугранные углы при боковых ребрах правильной усеченной пирамиды равны.
Площадь боковой поверхности усеченной пирамиды – сумма площадей
всех ее боковых граней. Обозначают Sбок
Площадь полной поверхности усеченной пирамиды – сумма площадей
всех ее граней. Обозначают Sполн
Усеченную пирамиду называют правильной, если она получена в результате сечения правильной пирамиды плоскостью, параллельной ее основанию.

Апофема правильной усеченной пирамиды – высота ее боковой грани (равнобокой трапеции).
Высота правильной усеченной пирамиды – отрезок, соединяющий центры ее оснований.
У правильной усеченной пирамиды:
Заполнить таблицу самостоятельно
Площадь поверхности и объём пирамиды
| Призма | Рисунок | Формулы для объема, площади боковой и полной поверхности |
| Пирамида | 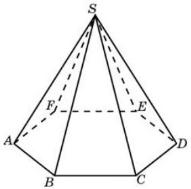
| V = … Sбок = … Sполн = … |
| Правильная пирамида | 
| V = … Sбок = … Sполн = …
|
| Усеченная пирамида | 
| V = … Sбок = … Sполн = …
|
| Правильная усеченная пирамида | 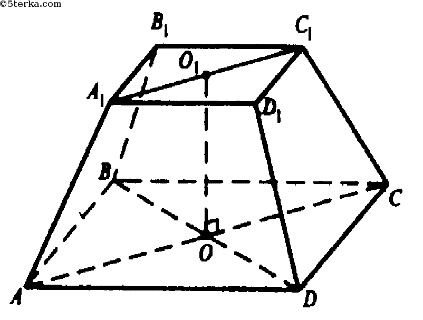
| V = … Sбок = … Sполн = …
|
































