Пирамида. Виды пирамид.

ПИРАМИДА

ПИРАМИДЫ

древности

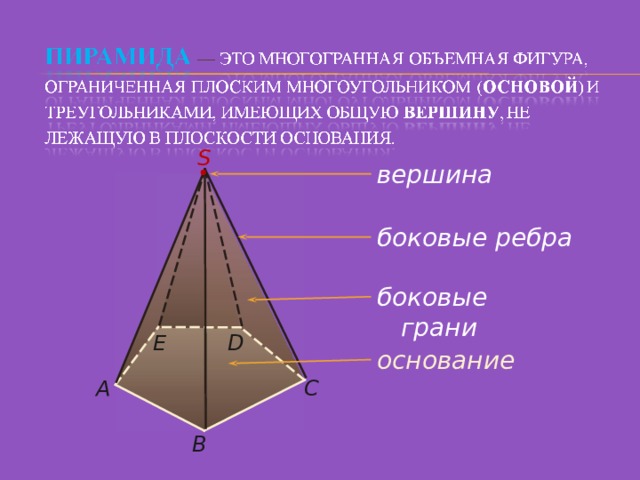
S

вершина

• вершина

боковые ребра

боковые грани

D

E

основание

C

А

B

ВИДЫ ПИРАМИД

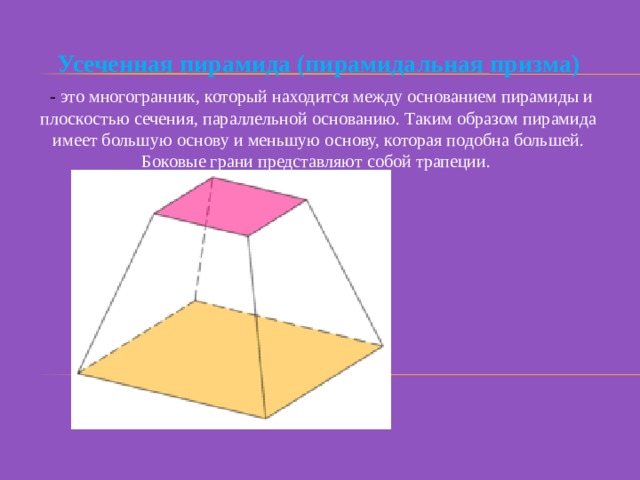
Усеченная пирамида (пирамидальная призма)

- это многогранник, который находится между основанием пирамиды и плоскостью сечения, параллельной основанию. Таким образом пирамида имеет большую основу и меньшую основу, которая подобна большей. Боковые грани представляют собой трапеции.

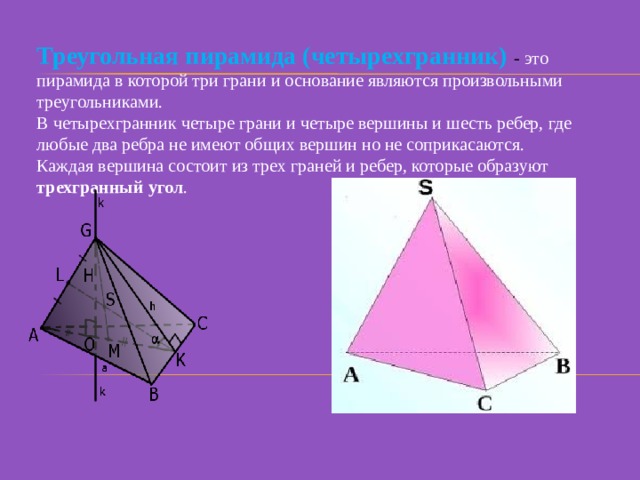
Треугольная пирамида (четырехгранник) - это пирамида в которой три грани и основание являются произвольными треугольниками.

В четырехгранник четыре грани и четыре вершины и шесть ребер, где любые два ребра не имеют общих вершин но не соприкасаются.

Каждая вершина состоит из трех граней и ребер, которые образуют трехгранный угол .

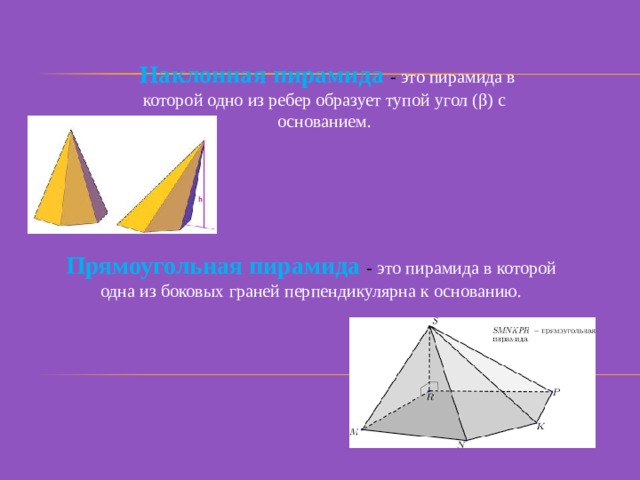
Наклонная пирамида - это пирамида в которой одно из ребер образует тупой угол (β) с основанием.

Прямоугольная пирамида - это пирамида в которой одна из боковых граней перпендикулярна к основанию.

Остроугольная пирамида - это пирамида в которой апофема больше половины длины стороны основания.

Тупоугольная пирамида - это пирамида в которой апофема меньше половины длины стороны основания.

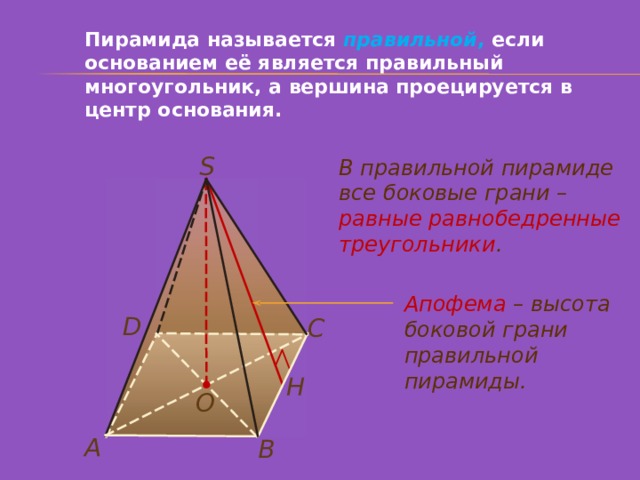
Пирамида называется правильной , если основанием её является правильный многоугольник, а вершина проецируется в центр основания.

S

В правильной пирамиде все боковые грани – равные равнобедренные треугольники .

Апофема  – высота боковой грани правильной пирамиды.

D

С

Н

О

А

В

ТЕОРЕМА О ПЛОЩАДИ БОКОВОЙ ПОВЕРХНОСТИ ПРАВИЛЬНОЙ ПИРАМИДЫ

Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему

S

S бок = ½ P осн  SH

l

D

С

Док – во:

S бок = (½al + ½al + ½al + … ) =

= ½ l (a + a + a + …)= ½Pl

Н

О

А

В

ПОСТРОЕНИЕ ПРАВИЛЬНЫХ ПИРАМИД

S

S

S

C

С

А

D

M

O

O

M

В

А

В

E

F

A

D

O

M

B

C

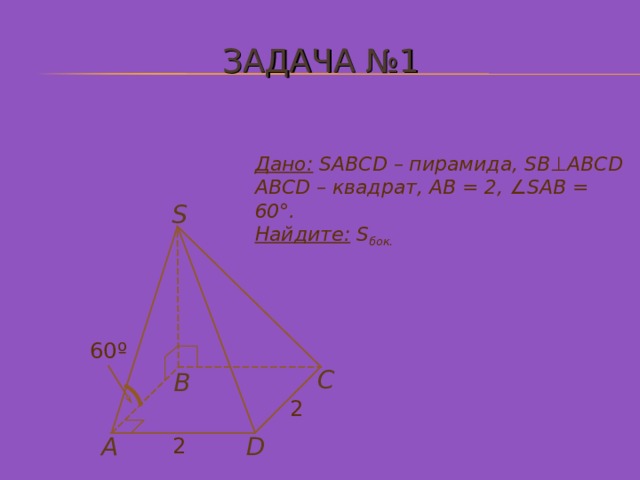
ЗАДАЧА №1

Дано: SABCD – пирамида, SB ⊥ ABCD

ABCD – квадрат, АВ = 2 , ∠SAB = 60°.

Найдите: S бок.

S

60º

С

В

2

А

D

2

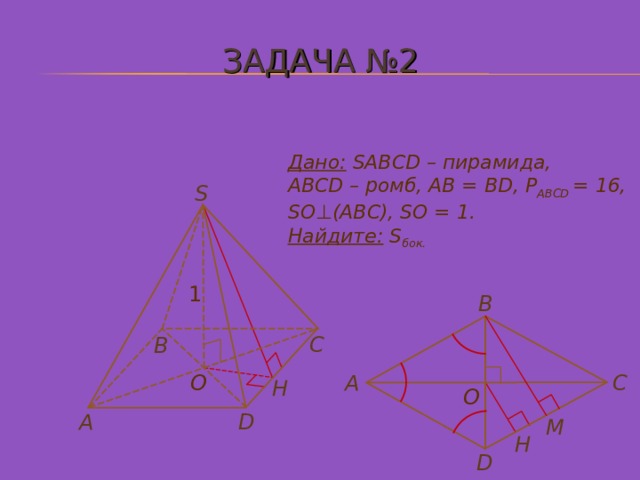
ЗАДАЧА № 2

Дано: SABCD – пирамида,

ABCD – ромб, АВ = BD, Р ABCD = 16,

SO ⊥ (АВС), SO = 1.

Найдите: S бок.

S

1

В

С

В

С

А

O

H

O

D

А

М

H

D

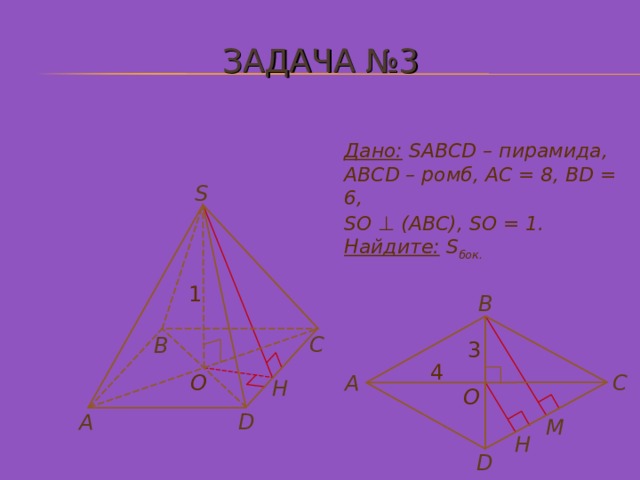
ЗАДАЧА № 3

Дано: SABCD – пирамида,

ABCD – ромб, АС = 8, BD = 6,

SO ⊥ (АВС), SO = 1.

Найдите: S бок.

S

1

В

С

В

3

4

С

А

O

H

O

D

А

М

H

D

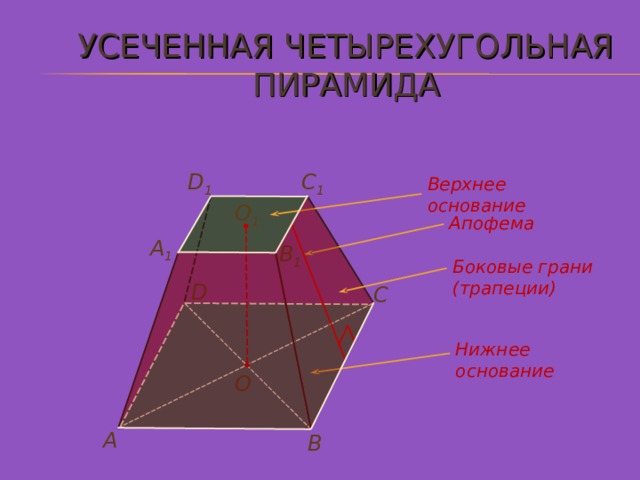
УСЕЧЕННАЯ ЧЕТЫРЕХУГОЛЬНАЯ ПИРАМИДА

C 1

D 1

Верхнее основание  

О 1

Апофема  

A 1

B 1

Боковые грани

(трапеции)  

D

С

Нижнее основание

О

А

В

площадь полной поверхности усеченной пирамиды

объем усеченной пирамиды

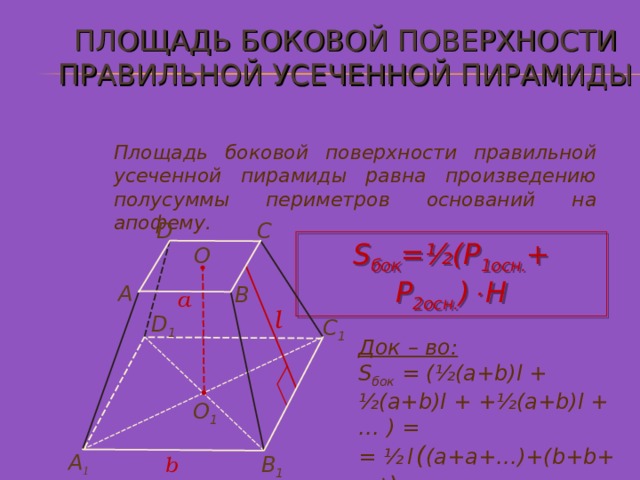
ПЛОЩАДЬ БОКОВОЙ ПОВЕРХНОСТИ ПРАВИЛЬНОЙ УСЕЧЕННОЙ ПИРАМИДЫ

Площадь боковой поверхности правильной усеченной пирамиды равна произведению полусуммы периметров оснований на апофему.

C

D

S бок =½ ( P 1осн. + P 2 осн. )  Н

О

A

B

a

l

D 1

С 1

Док – во:

S бок = (½(a+b)l + ½(a+b)l + +½(a+b)l + … ) =

= ½ l ( (a+a+…)+(b+b+…) ) =

=½ ( P 1осн. + P 2 осн. )  l

О 1

А 1

В 1

b

C 1

A 1

О 1

Н 1

В 1

С

А

F

О

E

Н

В