План конспект по теме "Простейшие тригонометрические уравнения"

6.9 «Решение простейших тригонометрических уравнений»

Чтобы уметь решать тригонометрические уравнения необходимо знать как минимум следующее:

• что такое синус, косинус, тангенс, котангенс;

• какие знаки принимает та или иная тригонометрическая функция в разных четвертях тригонометрической окружности;

• какие из этих функций нечётные, а какие – чётные;

• знание значений тригонометрических функций в основных углах 1 четверти.

Если ты что-то не знаешь, повтори следующие разделы:

• Синус, косинус, тангенс и котангенс угла и числа

• Тригонометрическая окружность

• Формулы тригонометрии

Простейшие тригонометрические уравнения

Что же это такое, как ты думаешь? Является ли, например, уравнение

22x−11=11 тригонометрическим?

Ты и сам прекрасно понимаешь, что нет! Потому что ни одной тригонометрической функции (sinx,cosx,tgx,ctgx) в нём и в помине нет!

А что насчёт вот такого уравнения?

sin2x+3x=2
И опять ответ отрицательный!

Это так называемое уравнение смешанного типа.

Оно содержит как тригонометрическую составляющую, так и линейную (3x).

Но вернёмся к вопросу: “Что же такое тригонометрические уравнения?”

Тригонометрические уравнения –это уравнения, в которых неизвестная находится строго под знаком тригонометрической функции!

Например:

• 6cos2x+5sinx−7=0

Однако для начала мы не будем решать сложные и иногда неприступные тригонометрические уравнения, а ограничимся самыми простыми уравнениями вида:

• sinf(x)=a

• cosf(x)=a

• tgf(x)=a

• ctgf(x)=a

Где a – некоторое постоянное число.

Например: 0,5; 1; −1;π;  1−3–√; 1000 и т. д.

f(x) – некоторая функция, зависящая от искомой переменной x, например f(x)=x, f(x)=2−x, f(x)=πx7 и т. д.

Такие уравнения называются простейшими!

Основная цель решения ЛЮБОГО тригонометрического уравнения – это свести его к виду простейшего!

Так что очень важно, я бы даже сказал, жизненно необходимо научиться решать простейшие уравнения, ибо они – фундамент для решения сложных примеров.

Как часто тригонометрические уравнения встречаются на ЕГЭ?

Тригонометрические уравнения могут встретиться до четырех раз в заданиях ЕГЭ. Это может быть:

• Задача №5 (простейшее тригонометрическое уравнение – встречается время от времени);

Так что, как ты понимаешь, при некоторых раскладах, навык решения данного вида уравнений может добавить в твою копилку аж 5 первичных баллов из 32!

Два способа решения тригонометрических уравнений – через формулы и по кругу

В принципе, я не могу сказать, что легче: держать в голове, как строится круг, или помнить 4 формулы.

Тут решать тебе самому, однако я всё же предпочитаю решать данные уравнения через формулы, поэтому здесь я буду описывать именно этот метод.

Вначале мы начнём с «самых простейших» из простейших уравнений вида:

• sinx=a,

• cosx=a,

• tgx=a,

• ctgx=a.

Я хочу сразу оговориться вот о чем, будь внимателен:

Уравнения вида: sinf(x)=a, cosf(x)=a имеют смысл только тогда, когда −1≤a≤1

Уравнения вида: tgx=a, ctgx=a имеют смысл уже при всех значениях a.

То есть, тебе не надо знать вообще никаких формул, чтобы спокойно ответить, что уравнения, например:

sinx=1000

cos(3x−sin(x))=2

sin(2x2−2x+1)=−3

Корней не имеют!!!

Почему?

Потому что они “не попадают” в промежуток от минус единицы до плюс единицы.

Для остальных же случаев тригонометрические формулы такие как в этой таблице.

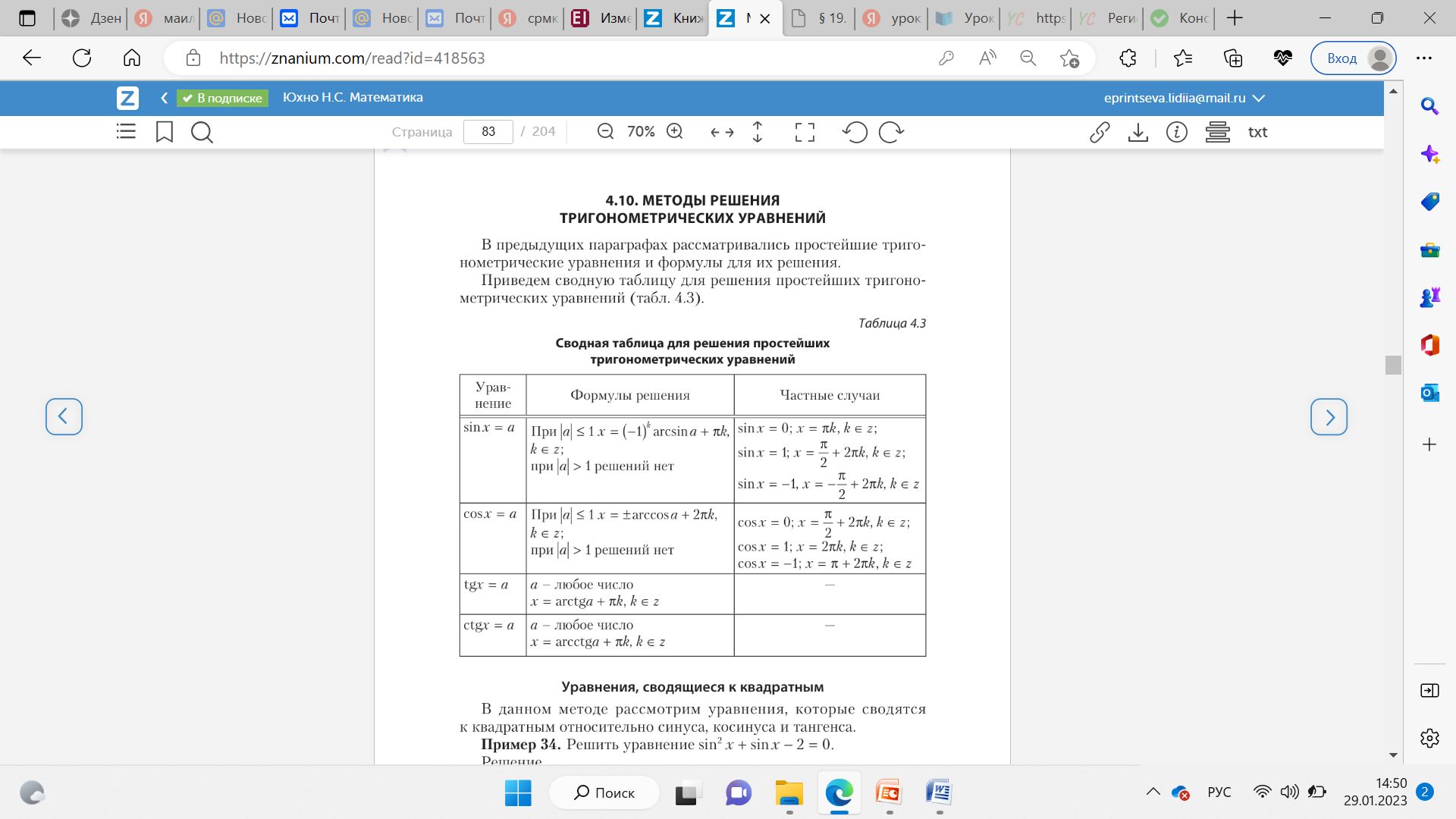
На самом деле в этой таблице данных немного больше, чем нужно.

Тебе нужно лишь запомнить первые два её столбца, другие столбцы – частные случаи решения тригонометрических уравнений.

Глядя на таблицу, не возникло ли у тебя пары вопросов?

У меня бы возникли вот какие:

Что такое n и что такое, например arcsinα (arccosα, arctgα, arcctgα)?

Отвечаю на все по порядку:

n – это любое целое число (0, 1, −1, 2, −2, …. ).

В чем уникальная особенность тригонометрических уравнений перед всеми остальными, которые ты изучал?

ОНИ ИМЕЮТ БЕСКОНЕЧНОЕ КОЛИЧЕСТВО КОРНЕЙ!!!

И число n и служит для обозначения этой «бесконечности».

Конечно, вместо n можно писать любую другую букву, только не забывай добавить в ответе: n∈Z – что означает, что n – есть любое целое число.

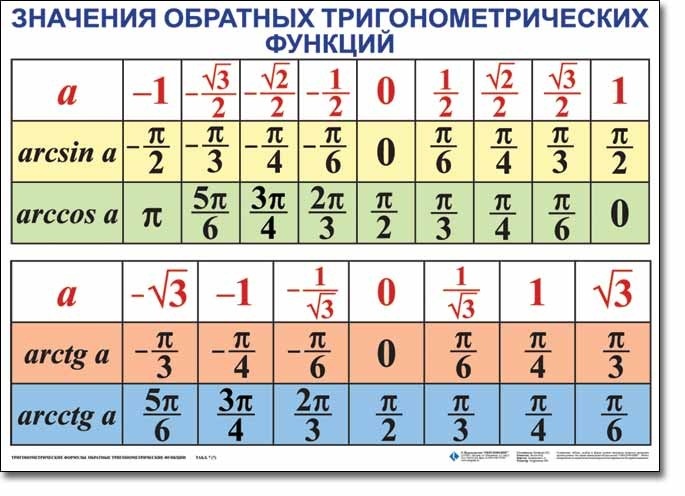
Теперь насчёт арксинуса и других «арок». Вообще, так записываются обратные тригонометрические функции и понимать, скажем, arcsinα надо как “угол, синус которого равен α“

• arcsinα– угол, синус которого равен α

• arccosα– угол, косинус которого равен α

• αarctgα– угол, тангенс которого равен α

• αarcctgα – угол, котангенс которого равен α

Например,

• arcsin(0)=0,

• arccos(2–√2)=π4,

•  arctg(1)=π4,

• arcsin(0,5)=π6,

• arccos(3–√2)=π6,

•  arctg(3–√)=π3

то есть,

Алгоритм вычисления арксинусов и других “арок”

• Смотрим на то, что стоит под «аркой» – какое там число

• Смотрим, какая у нас «арка» – для синуса ли, или для косинуса, тангенса или котангенса

• Смотрим, чему равен угол (1 четверти), для которого синус, косинус, тангенс, котангенс равен числу, стоящему под аркой

• Записываем ответ

Вот простой пример вычисления аркосинуса:

arccos(3–√2)

Решение:

• Под аркой число 3–√2

• Арка для функции – косинус!

• Косинус какого угла равен 3–√2? Угла π6 (или 30 градусов!)

• Тогда arccos(3–√2)=π6

Сам посчитай:

•  arctg(13–√)

• arcsin(3–√2)

Ответы:

π6 и π3.

Если “арка” берется от отрицательного числа?

Всё ли я сказал про “арки”? Почти что да! Остался вот какой момент.

Что делать, если “арка” берётся от отрицательного числа?

Лезть в таблицу – как бы не так! Для арок выполняются следующие формулы:

• arcsin(−α)=−arcsinα

• arctg(−α)=−arctgα

И внимание!!!

• arcctg(−α)= π −arcctgα

• arccos(−α)= π −arccosα

Чтобы запомнить, ориентируемся на обычные тригонометрические функции: грубо говоря, синус и тангенс мы смотрим на тригонометрической окружности по вертикальной оси, а косинус и котангенс – по горизонтальной.

Соответственно, для арксинуса и арктангенса выбираем две четверти по вертикали: первую и четвёртую (минусик выносится из аргумента и ставится перед функцией), а для арккосинуса и арккотангенса – по горизонтали: первую и вторую.

В первой и второй четвертях аргумент уже не может быть отрицательным, поэтому и получаются формулы не совсем похожими.

Ну всё, теперь мы можем приступать к решению простейших уравнений!