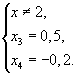Просмотр содержимого документа
«План урока по теме "Решения показательных и логарифмических уравнений."»
ПЛАН УРОКА№13 (1 курс)
УЧЕБНАЯ ДИСЦИПЛИНА МАТЕМАТИКА
КОЛИЧЕСТВО ЧАСОВ 1.
МЕСТО ПРОВЕДЕНИЯ КАБИНЕТ №22
ТЕМА ЗАНЯТИЯ: Логарифмические уравнения.
ЦЕЛИ ЗАНЯТИЯ: а) образовательная: Повторить свойства показательной и логарифмической функций. Отработать навыки решения показательных и логарифмических уравнений.
Проверить умение учащихся решать данные уравнения.
б) развивающая :Развивать мышление учащихся, умение анализировать условие задания, выделять различные этапы решения в нестандартных заданиях.
в) воспитательная : Воспитывать аккуратность, внимательность, умение обобщать изученный материал.
Ожидаемые результаты освоения темы:
Знать: свойства показательной и логарифмической функций, методы решения логарифмических и показательных уравнений.
Уметь: решать показательные и логарифмические уравнения.
Оснащение: Доска меловая, доска маркерная, карточки.
Основные этапы занятия:
Организация начала занятия.
Приветствие.
Проверка отсутствующих.
Знакомство с темой урока, совместное целеполагание.
Устное решение задач
а) определение логарифмического числа;
б) повторение свойств логарифма.
Вычислите следующие логарифмы:
| log5 5 | log8 1 | log3 27 | lg 1000 |
| log11 121 | 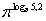
| 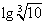
| 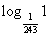
|
| 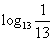
| 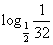
| 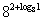
| 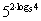
|
| log6 18 + log6 2 | log2 log3 81 | log3 18 - log3 2 | log9 0 |
| 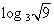
|
|
|
|
III. Решение уравнений
Программированный контроль, работает весь класс (готовые карточки для кодоскопа)
| 1 вариант | 2 вариант |
| При каких значениях x выражение имеет смысл |
| log3(x2 - 16) | log2(9 - x2) |
| Решите уравнение |
| log3(x2 - 5x + 33) = 3 | log2(x2 - 3x + 10) = 3 |
| log7(x + 1) = log7(2x - 3) | log6(x + 1) = log6(3x - 6) |
| 10lg(x - 16) - 1 | 2lg x + 3 0,5-5 |
Взаимопроверка.
IV Фронтальная работа (каждое задание решается учеником у доски с комментариями)
Решите уравнение:
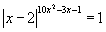
Решение:
∣x - 2∣ = 1,
x - 2 = 1 или x - 2 = -1
х1 = 3 или х2 = 1;
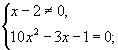
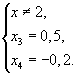
Ответ: -0,2; 0,5; 3; 1
Решите уравнение:
2∣3x - 5∣ = 4∙8∣x - 1∣
Решение:
Так как функция у = 2t – возрастает,
то ∣3x - 5∣ = 2 + 3∣x - 1∣.
при x ≤ 1 ,
-(3x - 5) = 2 - 3(x - 1)
-3x + 5 = 2 - 3x + 3
-3x + 3x = -5 + 5
0 = 0 - верно, значит x ≤ 1
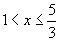
-(3x - 5) = 2 + 3(x - 1)
-3x + 5 = 2 + 3x - 3
-3x - 3x = -5 - 1
-6x = -1
x = 1- число не принадлежит промежутку.
при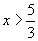
3x - 5 = 2 + 3(x - 1)
3x - 5 = 2 + 3x - 3
0∙x = 4- не верно, нет корней.
Ответ: (-∞; 1]
Решите уравнение:
log22(x - 1)2 = 5 + log0,5(x - 1)
log22(x - 1)2 - log0,5(x - 1) = 5
4∙log22(x - 1)2 + log2(x - 1) = 5
О.Д.З. x - 1 0, т.е. x 1
Пусть log2(х - 1) = t, тогда 4t2 + t - 5 = 0
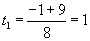
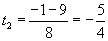
log2(x - 1) = 1 или log2(x - 1) = -5 / 4
log2(x - 1) = log2 2 или log2(x - 1) = log2 2-5 / 4
| x - 1 = 2 или | 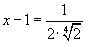
|
| x = 3 или | 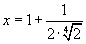
|
| Ответ: 3; | 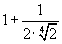
|
|
|
|
V. Самостоятельная работа по тестам, с последующей самопроверкой (Приложение)
Ответы к тестам:
| № задания | 1 | 2 | 3 | 4 |
| Ответ | 1 | 2 | 2 | 4 |
Учащиеся проверяют друг друга правильность выполнения заданий и выставляют оценки.
Критерии оценок:
| "5" | 4 правильно выполненных задания |
| "4" | 3 правильно выполненных задания |
| "3" | 2 правильно выполненных задания |
| "2" | менее 2 правильно выполненных задания |
VI. Задание на дом: Б.З: 12.6А(1-7)
VII.Рефлексия. Подведение итогов урока
Мы повторили основные методы решения показательных, логарифмических уравнений, что поможет при написании контрольной работы, сдаче экзамена.