Площадь круга и кругового сектора

УЧЕБНЫЙ ПРОЕКТ

ПО МАТЕМАТИКЕ

РАЗДЕЛ: ГЕОМЕТРИЯ

НА ТЕМУ:

«ПЛОЩАДЬ КРУГА И КРУГОВОГО СЕКТОРА»

Работу выполнила ученица

9 класса «В»

Миронова Виктория

Площадь круга

Формы круга, окружности мы встречаем повсюду: это и колесо машины, и линия горизонта, и диск Луны.

Математики стали заниматься геометрической фигурой - кругом на плоскости - очень давно.

Кругом с центром О и радиусом R называется множество точек плоскости, удаленных от O на расстояние, не большее R. Круг ограничен окружностью, состоящей из точек, удаленных от центра O в точности на расстояние R. Отрезки, соединяющие центр с точками окружности, имеют длину R и также называются радиусами (круга, окружности). Части круга, на которые он делится двумя радиусами, называются круговыми секторами

Еще в древности пытались решить задачи, связанные с кругом, - измерить длину окружности или ее дуги, площадь круга или сектора, сегмента. Первая из них имеет чисто «практическое» решение: можно уложить вдоль окружности нить, а потом развернуть ее и приложить к линейке или же отметить на окружности точку и «прокатить» ее вдоль линейки (можно, наоборот, «обкатить» линейкой окружность).

Так или иначе измерения показывали, что отношение длины окружности  C к ее диаметру d=2R одно и то же для всех окружностей. Это отношение принято обозначать греческой буквой π («пи» - начальная буква греческого слова perimetron, которое и означает «окружность»).

В 2002 году японский ученый вычислил 1240000 миллиона цифр числа "пи" с

помощью мощного компьютера, побив все предыдущие рекорды. К 2000 году до н.э., вавилоняне вычислили постоянную отношения радиуса к окружности - 3-1/8 или 3,125. Древние египтяне нашли немного другое отношение - 3-1/7 или 3.143. Интересный факт, день "ПИ" отмечается 14 марта (который был выбран потому, что напоминает 3.14). Официальное празднование начинается в 1:59 часов вечера, чтобы сделать 3,14159 в сочетании с датой. Уильям Джонс (1675-1749) ввел символ "π" в 1706 году. Альберт Эйнштейн родился в день ПИ

Современные математики могут получить площадь круга с помощью методов интегрирования или вещественного анализа. Однако площадь круга изучалась ещё в Древней Греции. Евдок Книдский в пятом столетии до нашей эры обнаружил, что площади кругов пропорциональны квадратам их радиусов.

Великий математик Архимед использовал методы евклидовой геометрии, чтобы показать, что площадь внутри окружности равна площади прямоугольного треугольника, основание которого имеет длину окружности, а высота равна радиусу окружности, в своей книге «Измерение круга». Длина окружности равна 2π r , а площадь треугольника равна половине основания на высоту, что даёт π r 2 . До Архимеда Гиппократ Хиосский первый показал, что площадь круга пропорциональна квадрату его диаметра в его попытках квадрирования гиппократовых луночек. Однако он не установил константу пропорциональности.

Пусть дана окружность с радиусом R= 4 см.

Найдем площадь фигуры.

S=3,14×4^2=3,14×16=50,24

Площадь нашей окружности будет равна 50,24 кв. см.

Существует формула  площади круга через диаметр .

Она также широко применяется для вычисления необходимых параметров. S= d 2

Рассмотрим пример расчета площади круга через диаметр, зная его радиус.

Пусть дана окружность с радиусом R = 4 см.

Для начала найдем диаметр, который, как известно, в два раза больше радиуса.

d=2R d=2×4=8

Теперь используем данные для примера расчета площади круга по приведенной выше формуле:

S= *8 2 =0,785×64=50,24

Как видим, в результате получаем тот же ответ, что и при первых расчетах.

Знания стандартных формул расчета площади круга помогут в дальнейшем легко определять площадь секторов и легко находить недостающие величины.

Мы уже знаем, что формула площади круга рассчитывается через произведение постоянной величины π на квадрат радиуса окружности. Радиус можно выразить через длину окружности и подставить выражение в формулу площади круга через длину окружности: R= π

Теперь подставим это равенство в формулу расчета площади круга и получим формулу нахождения площади круга, через длину окружности S=π( π) 2 =

Рассмотрим пример расчета площади круга через длину окружности. Пусть дана окружность с длиной l= 8 см.

Подставим значение в выведенную формулу:

S=

Итого площадь круга будет равна 5 кв. см.

=

=

5

Почему площадь круга равна πr^2?

То, что площадь круга равна πr 2 доказал Архимед еще во втором столетии до нашей эры, но как ему удалось это сделать? Пожалуй, в ответе на этот вопрос мне поможет пицца.

Представьте, что вы живете в Древней Греции и вы решили пообедать пиццей. Вы разрезали ее на 8 частей и... задумались. А что будет, если выложить все кусочки в один ряд? Получится примерно такая картина:

Тут вы понимаете, что эта фигура отдаленно начинает напоминать параллелограмм, а длина стороны кусочка равна радиусу пиццы (круга). Верхушка её равна половине длины окружности, то есть просто π.

РЕШЕНИЕ ЗАДАЧ ПО ГОТОВЫМ ЧЕРТЕЖАМ

НАЙДИТЕ ПЛОЩАДЬ КРУГА:

1) Для начала выразим радиус окружности

S круга=πr 2 , πr 2 = 2 πr

приравняем площадь круга в к длине окружности (С)=4

2πr=4

2=πr

r =

S=π( ) 2 S=4

треугольник АОВ – равносторонний ,значит радиус окружности = 8

S круга

S=64π

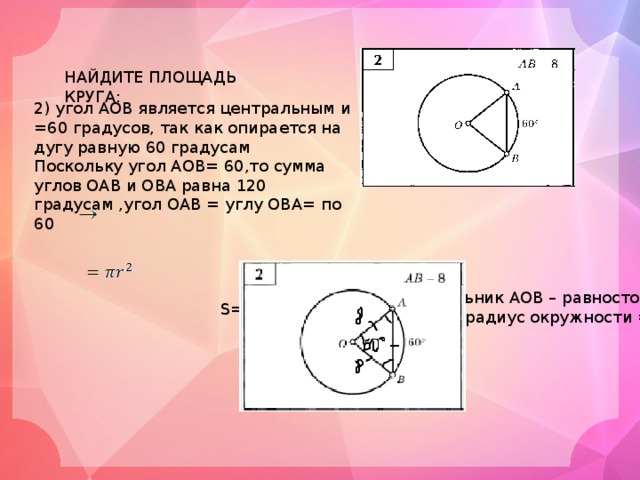
НАЙДИТЕ ПЛОЩАДЬ КРУГА:

2) угол АОВ является центральным и =60 градусов, так как опирается на дугу равную 60 градусам

Поскольку угол АОВ= 60,то сумма углов ОАВ и ОВА равна 120 градусам ,угол ОАВ = углу ОВА= по 60

НАЙДИТЕ ПЛОЩАДЬ КРУГА:

4) Проведём высоту СН ,ОН - радиус окружности , АН=НВ=6

по теореме Пифагора найдём СН, она будет равна 6

так как треугольник АВС равносторонний то СО:ОН как 2:1 , 2+1=3 части всего

6 :3=2 -1 часть

1 часть = ОН радиус окружности =2 , S круга = πr 2

S= π (2 ) 2 S=12π

Найти площадь круга, если его радиус равен 2 см.

Так как площадь круга равна  π  умноженное на радиус в квадрате, то площадь круга с радиусом 2 см будет равна:

S  ≈ 3,14 · 2 2  = 3,14 · 4 = 12,56 (см 2 )

Найти площадь круга, если его диаметр равен 7 см.

Сначала найдём радиус круга, разделив его диаметр на 2:

7 : 2 = 3,5 (см)

теперь вычислим площадь круга по формуле:

S  =  πr 2  ≈ 3,14 · 3,5 2  = 3,14 · 12,25 = 38,465 (см 2 )

Площадь кругового сектора

Площадь кругового сектора тоже выражается через число π.

Круговым сектором называется часть круга, ограниченная двумя радиусами и дугой между ними (рис. 1).

Фигура, которая получается в пересечении круга и его центрального угла, называется круговым сектором.

Мы видим, что сектор – это криволинейный треугольник AOB, два радиуса OA и OB, угол AOB центральный, угол  a , длина дуги  и площадь (рис. 1).

Круг задается одним элементом – радиусом, для того чтобы задать сектор, необходимо задать два элемента, например радиус и угол.

Рис. 1. Круговой сектор

Решение задач

Дано: 

Найти: 

Решение

Площадь сектора – это часть площади круга (рис. 2), площадь круга – , сектор, центральный угол которого равен 360 градусов , разделим на  360 градусов

Получим площадь сектора, у которого угол равен  1 градус , а их  a  градусов, значит, нужно умножить на  a :

Аналогично находим длину дуги :

Поучаем длину дуги, которая соответствует центральному углу в 1 градус , а их  a  градусов, значит, нужно умножить на  a :

Рис. 2. Круг и круговой сектор, ограниченный двумя радиусами

Дано: 

Найти: 

Решение

Рис. 3. Круговой сектор