Площадь многоугольника

Площадь многоугольника.

Презентацию выполнил:

учитель математики ГБОУ СОШ № 457

Вдовина Наталья Борисовна

Свойства площадей многоугольников.

• 1.Равные многоугольники имеют равные площади.
• 2.Если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников.
• 3.Площадь квадрата равна квадрату его стороны.

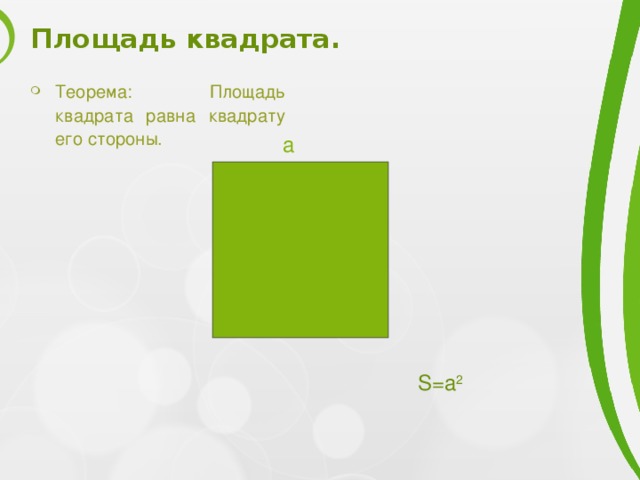
Площадь квадрата.

• Теорема: Площадь квадрата равна квадрату его стороны.

a

S=a 2

Задача.

Найдите сторону квадрата,площадь которого равна площади прямоугольника со смежными сторонами 8 м и 18 м.

Дано:Sкв.=Sпрямоуг.

a=8 м, b=18 м.

Найти: c-?.

a

c

b

Решение: т.к . Sкв.=Sпрямоуг..=a*b=18*8=144 м

Sкв.=c 2 c=√S

c=√144

c=12 м

Ответ:c=12 м.

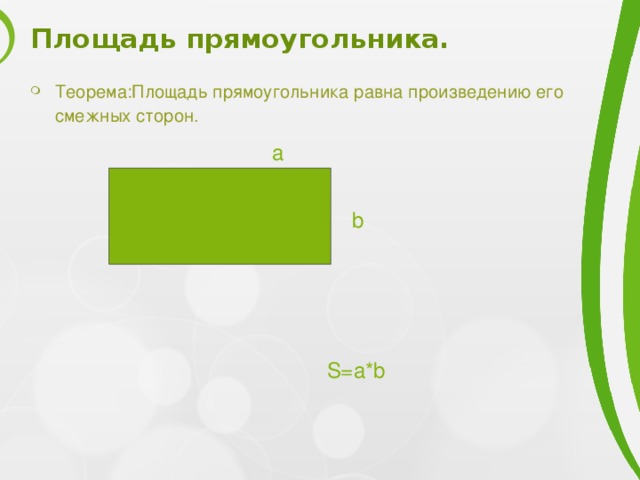
Площадь прямоугольника.

• Теорема:Площадь прямоугольника равна произведению его смежных сторон.

a

b

S=a*b

Задача.

• Найдите стороны прямоугольника, если его площадь равна 250 см 2 , а одна сторона в 2,5 раза больше другой.

b

Дано: Sпрямоуг.=250 см 2 ,

b-?, в 2,5 р. б. стороны a.

Найти: a-?,

b-?.

a

Решение: S=a*b

Пусть x - a,

b=2,5x

x*2,5x=250

2,5x 2 =250

x=√250*2,5

x=√100

x=10 см - a

2,5x=25 см - b

Ответ: a=10 см,b=25 см.

h b

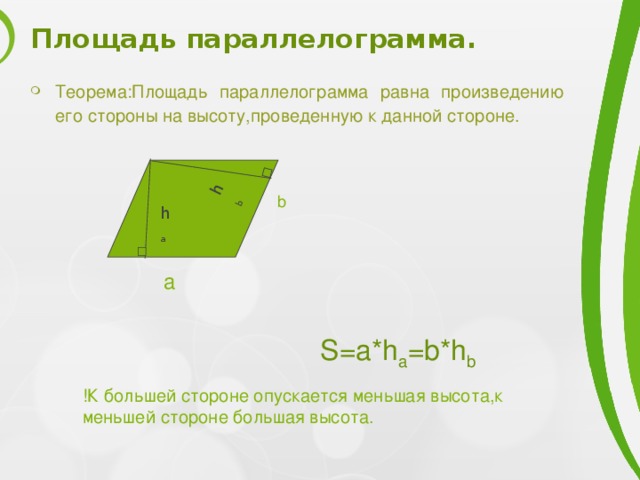
Площадь параллелограмма.

• Теорема:Площадь параллелограмма равна произведению его стороны на высоту,проведенную к данной стороне.

b

h a

a

S=a*h a =b*h b

!К большей стороне опускается меньшая высота,к меньшей стороне большая высота.

Задача.

• Пусть a-основание,h-высота,а S-площадь параллелограмма.Найдите h,если h=3a,S=27.

Дано:h=3a,S=27.

Найти:h-?

h

Решение: S=a*h

S=a*3a

27=3a 2 :3

a 2 =9

a=√9

a=3

h=S:a

h=27:3=9

Ответ: h=9.

a

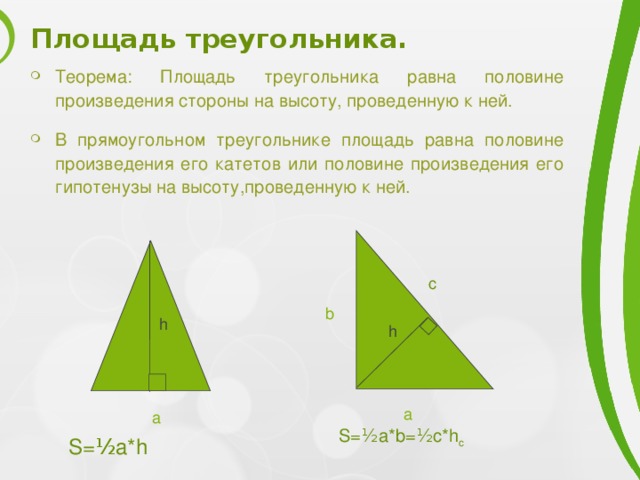
Площадь треугольника.

• Теорема: Площадь треугольника равна половине произведения стороны на высоту, проведенную к ней.
• В прямоугольном треугольнике площадь равна половине произведения его катетов или половине произведения его гипотенузы на высоту,проведенную к ней.

c

b

h

h

a

a

S= ½ a*b= ½ c*h c

S= ½ a*h

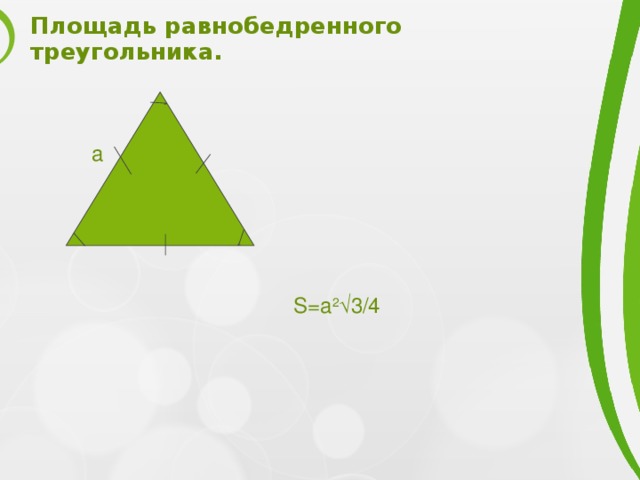
Площадь равнобедренного треугольника.

a

S=a 2 √3/4

Задача.

• Найти площадь равностороннего треугольника , если известно, что его сторона равна 2 дм.

Дано:a=2 дм.

Найти:S△-?.

a

Решение: S=a 2 √3/4

S△=2 2 √3/4

S△=4√3/4

S△=√3 дм 2

Ответ:S△=√3 дм 2 .

Формула Герона.

b

a

c

Площадь S треугольника со сторонами a,b,c выражается формулой S=√p*(p-a)*(p-b)*(p-c),где p=½*(a+b+c) - полупериметр треугольника.

Задача.

• Вычислите площадь треугольника, зная, что его стороны равны 6 см; 5 см и 2,2 см.

Дано:

a=6 см,

b=5 см,

c=2,2 см.

Найти:S△-?

b

a

c

Решение:p=½*(a+b+c)

p=½*(6 см+5 см+2,2 см)=6,6 см.

S△=√p*(p-a)*(p-b)*(p-c)

S△=√6,6*(6,6-6)*(6,6-5)*(6,6-2,2)=√6,6*0,6*1,6*4,4=√27,8784=5,28 см 2 .

Ответ:S△=5,28 см 2 .

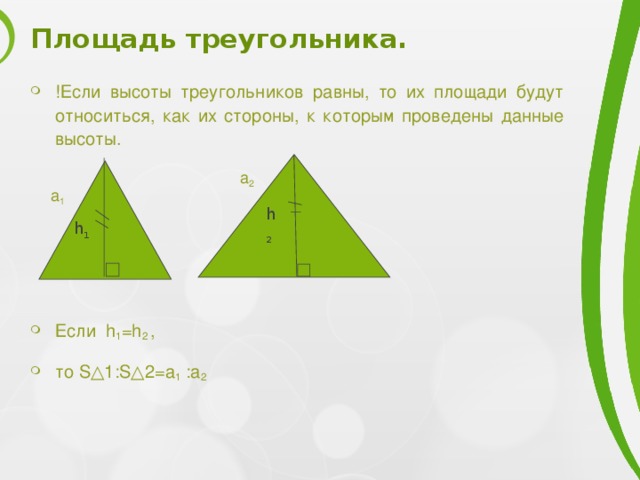
Площадь треугольника.

• !Если высоты треугольников равны, то их площади будут относиться, как их стороны, к которым проведены данные высоты.
• Если h 1 =h 2 ,
• то S△1:S△2=a 1 :a 2

a 2

a 1

h 2

h 1

Площадь треугольника.

• Если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведения сторон,заключающих равные углы.

B1

B

C1

A1

A

C

если

то S△ ABC /S△ A1B1C1 =(AB*AC)/A 1 B 1 *A 1 C 1

Задача.

• Пусть a-основание,h-высота,а S-площадь треугольника.Найдите S,если a=2√3 см, h=5 см.

Дано: a=2√3 см,

h=5 см.

Найти:S-?.

h

a

Решение: S= ½ a*h

S= ½ *2√3*5=5√3 см 2

Ответ: S= 5√3 см 2 .

Площадь трапеции.

• Теорема: Площадь трапеции равна произведению полусуммы оснований на высоту.
• !Высоты трапеции - высоты, опущенные к основаниям.
• !В прямоугольной трапеции высотой является боковая сторона с прямым углом.
• !Все высоты трапеций равны между собой.

a

h

S=½*(a+b)*h

b

Задача.

• Найдите площадь трапеции ABCD с основаниями AB и CD если

B

A

Дано:ABCD-трапеция,

AB,CD-основания,

Найти:Sabcd-?.

C

D

F

Решение: Проведем AF-высоту,

тогда △ AFD - прямоуг.

AF=4,

S abcd = ½ *(AB+CD)*AF= ½ *(2+10)*4=6*4=24см 2

Ответ:S abcd =24см 2.

Площадь ромба.

d1

d2

h

a

a

S=a*h a

S= ½ d1*d2

Где h-высота,

a-сторона

d1,d2-диагонали

Задача.

• Вычислите площадь ромба,если его диагонали равны 4,6 дм и 2 дм.

Дано:d1=4,6 дм,

d2=2 дм.

Найти:S ромба -?

d1

d2

Решение:S= ½ d1*d2

S= ½ *4,6*2=4,6 дм 2 .

Ответ:S=4,6 дм 2 .