ПЛОЩАДИ ФИГУР
Квадрат
1.
Сторона квадрата равна 10. Найдите его площадь.
Ответ: 100
2.
Периметр квадрата равен 40. Найдите площадь квадрата.
Ответ: 100
3.

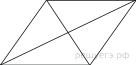
Из квадрата вырезали прямоугольник (см. рисунок). Найдите площадь получившейся фигуры.
Ответ: 28
4.
 Периметр квадрата равен 160. Найдите площадь квадрата.
Периметр квадрата равен 160. Найдите площадь квадрата.
Ответ: 1600
5.
 Найдите площадь квадрата, если его диагональ равна 1.
Найдите площадь квадрата, если его диагональ равна 1.
Ответ: 0,5
6.
 Найдите площадь квадрата, описанного вокруг окружности радиуса 83.
Найдите площадь квадрата, описанного вокруг окружности радиуса 83.
Ответ: 27556
Прямоугольник
1.
В прямоугольнике одна сторона равна 10, другая сторона равна 12. Найдите площадь прямоугольника.
Решение.
Площадь прямоугольника равна произведению его смежных сторон, поэтому она равна 120.
Ответ: 120.
2.
В прямоугольнике диагональ равна 10, а угол между ней и одной из сторон равен 30°. Найдите площадь прямоугольника, делённую на 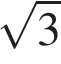 .
.
Решение.
Диагональ прямоугольника делит его на два прямоугольных треугольника. Катет прямоугольного треугольника, лежащий напротив угла в 30°, равен половине гипотенузы. Поэтому одна из сторон прямоугольника равна 5. По теореме Пифагора найдем вторую строну: 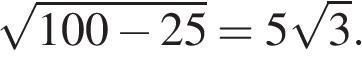 Площадь прямоугольника равна произведению его смежных сторон, имеем:
Площадь прямоугольника равна произведению его смежных сторон, имеем:
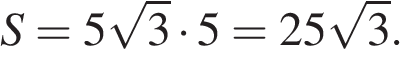
Ответ: 25.
3. В прямоугольнике диагональ равна 10, угол между ней и одной из сторон равен 30°, длина этой стороны  . Найдите площадь прямоугольника, деленную на
. Найдите площадь прямоугольника, деленную на 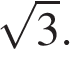
Решение.
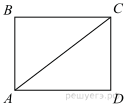
Диагональ прямоугольника делит его на два прямоугольных треугольника. Катет, лежащий напротив угла в 30°, равен половине гипотенузы, поэтому СD = 5. Площадь прямоугольника равна произведению его смежных сторон:
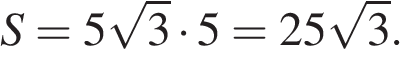
Ответ: 25.
Примечание:
Вторую сторону можно было найти из определения синуса.
4.
Найдите площадь прямоугольника, если его периметр равен 44 и одна сторона на 2 больше другой.
Решение.
Площадь прямоугольника равна произведению его сторон. Найдём стороны прямоугольника. Пусть x — меньшая сторона прямоугольника. Тогда периметр прямоугольника равен 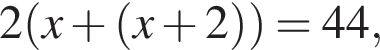 откуда
откуда 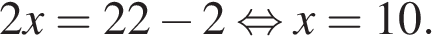 Поэтому площадь прямоугольника равна
Поэтому площадь прямоугольника равна 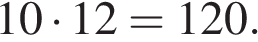
Ответ: 120.
5.
Найдите площадь прямоугольника, если его периметр равен 60, а отношение соседних сторон равно 4:11.
Решение.
Площадь прямоугольника равна произведению его сторон. Найдём стороны прямоугольника. Пусть x — большая сторона прямоугольника, тогда другая сторона равна 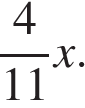 Следовательно, периметр прямоугольника равен
Следовательно, периметр прямоугольника равен
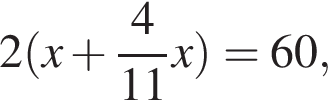
откуда 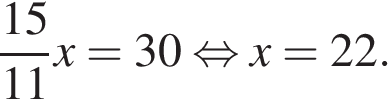 Поэтому площадь прямоугольника равна
Поэтому площадь прямоугольника равна 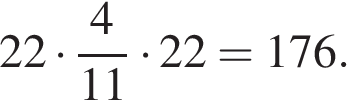
Ответ: 176.
6.
Найдите площадь прямоугольника, если его периметр равен 58 и одна сторона на 5 больше другой.
Решение.
Площадь прямоугольника равна произведению его сторон. Найдём стороны прямоугольника. Пусть x — меньшая сторона прямоугольника, тогда другая сторона равна  Следовательно, периметр прямоугольника равен
Следовательно, периметр прямоугольника равен
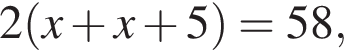
откуда  Поэтому площадь прямоугольника равна
Поэтому площадь прямоугольника равна 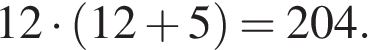
Ответ: 204.
7.
 В прямоугольнике одна сторона равна 96, а диагональ равна 100. Найдите площадь прямоугольника.
В прямоугольнике одна сторона равна 96, а диагональ равна 100. Найдите площадь прямоугольника.
Решение.
Пусть a и b — длины сторон прямоугольника, c — длина диагонали. Рассмотрим прямоугольный треугольник, образованный диагональю и сторонами треугольника, из теоремы Пифагора найдём вторую сторону прямогуольника:
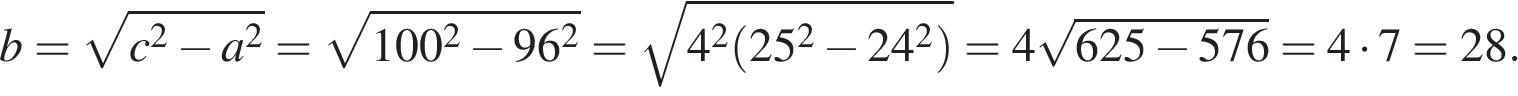
Найдём площадь прямоугольника как произведение его сторон:
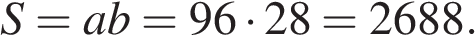
Ответ: 2688.
Прямоугольный треугольник
1.
В прямоугольном треугольнике один из катетов равен 10, а угол, лежащий напротив него, равен 45°. Найдите площадь треугольника.
Решение.
Так как в прямоугольном треугольнике один из углов равен 45°, то такой треугольник является равнобедренным. Площадь прямоугольного треугольника равна половине произведения катетов. Таким образом:
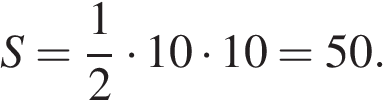
Ответ: 50.
Ответ: 50
2. Задание 18 № 323159
Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 28 и 100.
Решение.
Пусть катеты имеют длины 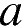 и
и 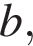 а гипотенуза — длину
а гипотенуза — длину 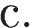 Пусть длина высоты, проведённой к гипотенузе равна
Пусть длина высоты, проведённой к гипотенузе равна 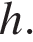 Найдём длину неизвестного катета из теоремы Пифагора:
Найдём длину неизвестного катета из теоремы Пифагора:
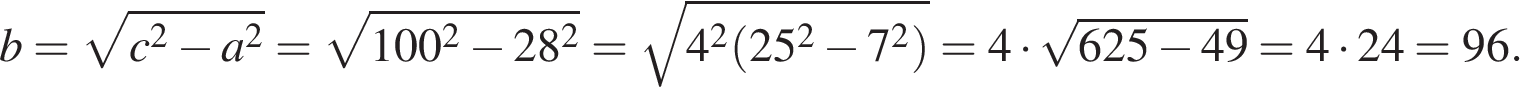
Площадь прямоугольного треугольника может быть найдена как половина произведения катетов:
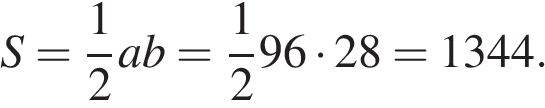
Ответ: 1344.
Ответ: 1344
3. Задание 18 № 323282
В прямоугольном треугольнике один из катетов равен 4, а острый угол, прилежащий к нему, равен 45°. Найдите площадь треугольника.
Решение.
Сумма углов в треугольнике равна 180°, поэтому второй острый угол равен 180° − 90° − 45° = 45°. Оба острых угла равны, следовательно, данный треугольник — равнобедренный, откуда получаем, что второй катет равен 4. Площадь прямоугольного треугольника можно найти как половину произведения катетов: 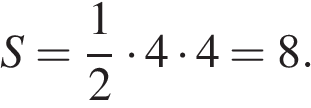
Ответ: 8.
4.
 В прямоугольном треугольнике гипотенуза равна 70, а один из острых углов равен 45°. Найдите площадь треугольника.
В прямоугольном треугольнике гипотенуза равна 70, а один из острых углов равен 45°. Найдите площадь треугольника.
Решение.
Сумма углов в треугольнике равна 180°, поэтому второй острый угол равен 180° − 90° − 45° = 45°. Оба острых угла равны, следовательно, данный треугольник — равнобедренный, откуда получаем, что оба катета равны. Длина катета равна 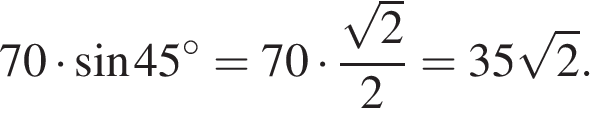 Площадь прямоугольного треугольника можно найти как половину произведения катетов:
Площадь прямоугольного треугольника можно найти как половину произведения катетов: 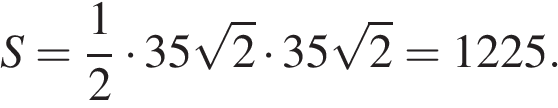
Ответ: 1225.
5.
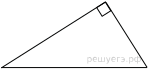
Два катета прямоугольного треугольника равны 4 и 9. Найдите площадь этого треугольника.
Решение.
Площадь прямоугольного треугольника равна половине произведения катетов. Таким образом:
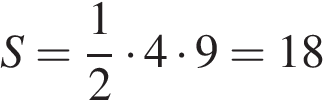
Ответ: 18
Равнобедренный треугольник
1.
Сторона равностороннего треугольника равна 10. Найдите его площадь, делённую на 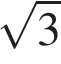 .
.
Решение.
Площадь треугольника равна половине произведения сторон на синус угла между ними. Так как угол равностороннего треугольника равен 60° и все стороны равны 10, имеем:
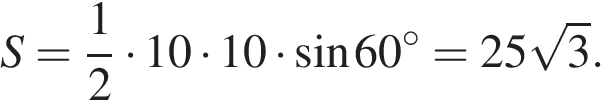
Ответ: 25.
2. Периметр равностороннего треугольника равен 30. Найдите его площадь, делённую на 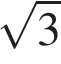 .
.
Решение.
Так как в равностороннем треугольнике все стороны равны, то сторона данного треугольника равна 10. Угол равностороннего треугольника равен 60°. Площадь треугольника равна половине произведения сторон на синус угла между ними, имеем:
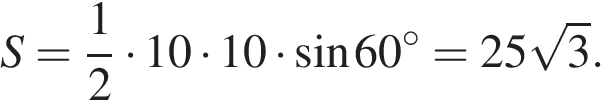
Ответ: 25.
3.
Высота равностороннего треугольника равна 10. Найдите его площадь, делённую на 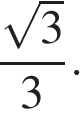
Решение.
Высота равностороннего треугольника равна 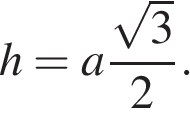 Таким образом, сторона равностороннего треугольника равна
Таким образом, сторона равностороннего треугольника равна 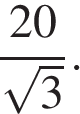 Площадь треугольника равна половине произведения сторон на синус угла между ними. Имеем:
Площадь треугольника равна половине произведения сторон на синус угла между ними. Имеем:
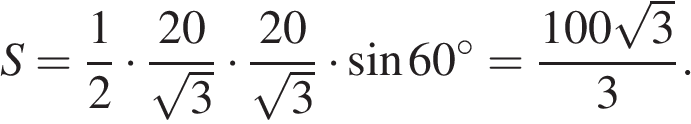
Ответ: 100.
4.
В равнобедренном треугольнике боковая сторона равна 10, а угол, лежащий напротив основания, равен 120°. Найдите площадь треугольника, делённую на 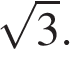
Решение.
Площадь треугольника равна половине произведения сторон на синус угла между ними, имеем:
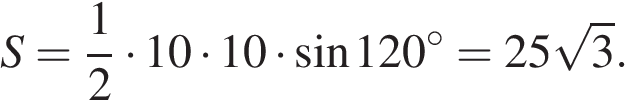
Ответ: 25.
5.
Периметр равнобедренного треугольника равен 16, а боковая сторона — 5. Найдите площадь треугольника.
Решение.
Так как боковая сторона равнобедренного треугольника равна 5, его основание равно 6, а полупериметр: 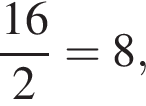 по формуле Герона имеем:
по формуле Герона имеем:

Ответ: 12.
Приведём другое решение.
Найдя основание и боковые стороны равнобедренного треугольника, находим по теореме Пифагора высоту, она равна 4. Далее по формуле площади треугольника, находим, что она равна 12.
6.
В равнобедренном треугольнике боковая сторона равна 10, основание — 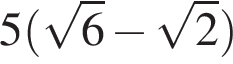 , а угол, лежащий напротив основания, равен 30°. Найдите площадь треугольника.
, а угол, лежащий напротив основания, равен 30°. Найдите площадь треугольника.
Решение.
Площадь треугольника равна половине произведения сторон на синус угла между ними:
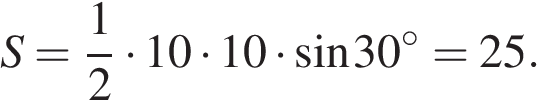
Ответ: 25.
Примечание:
Площадь треугольника можно было найти по формуле Герона.
7.
 Боковая сторона равнобедренного треугольника равна 34, а основание равно 60. Найдите площадь этого треугольника.
Боковая сторона равнобедренного треугольника равна 34, а основание равно 60. Найдите площадь этого треугольника.
Решение.
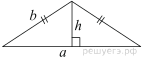 Пусть
Пусть 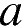 — длина основания равнобедренного треугольника,
— длина основания равнобедренного треугольника, 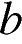 — длина боковой стороны равнобедренного треугольника,
— длина боковой стороны равнобедренного треугольника, 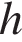 — высота, проведенная к основанию
— высота, проведенная к основанию 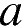 . Высота равнобедренного треугольника, проедённая к основанию, также является его биссектрисой и медианой. Из прямоугольного треугольника найдём высоту по теореме Пифагора:
. Высота равнобедренного треугольника, проедённая к основанию, также является его биссектрисой и медианой. Из прямоугольного треугольника найдём высоту по теореме Пифагора:
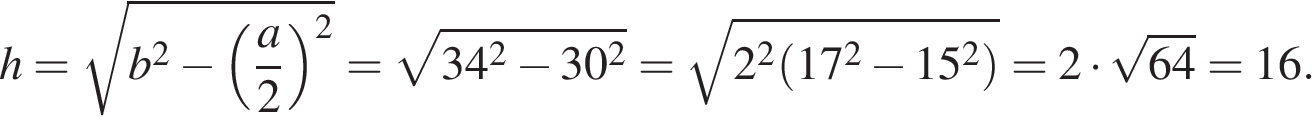
Площадь треугольника равна половине произведения основания на высоту:
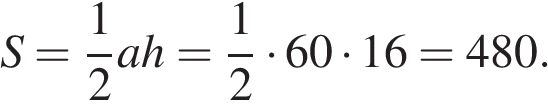
Ответ: 480.
8.
 Периметр равнобедренного треугольника равен 216, а боковая сторона — 78. Найдите площадь треугольника.
Периметр равнобедренного треугольника равен 216, а боковая сторона — 78. Найдите площадь треугольника.
Решение.
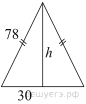 Периметр треугольника равен сумме длин его сторон, поэтому длина основания равна 216 − 78 − 78 = 60. Высота
Периметр треугольника равен сумме длин его сторон, поэтому длина основания равна 216 − 78 − 78 = 60. Высота 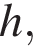 проведённая к основанию равнобедренного треугольника, также является его биссектрисой и медианой, поэтому (см. рис.) имеем:
проведённая к основанию равнобедренного треугольника, также является его биссектрисой и медианой, поэтому (см. рис.) имеем:
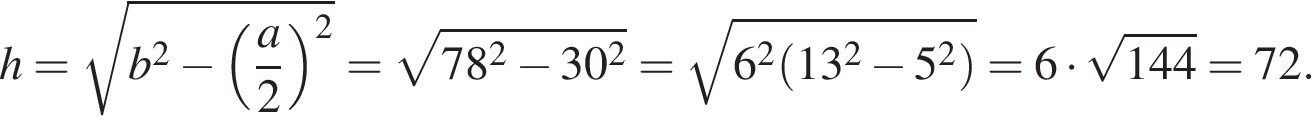
Площадь треугольника равна половине произведения основания на высоту:
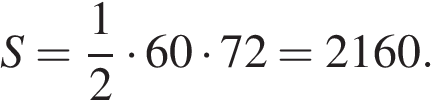
Ответ: 2160.
Примечание.
Пусть 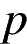 — полупериметр треугольника,
— полупериметр треугольника, 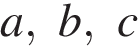 — стороны треугольника. Можно не находить высоту, а найти площадь по формуле Герона:
— стороны треугольника. Можно не находить высоту, а найти площадь по формуле Герона:
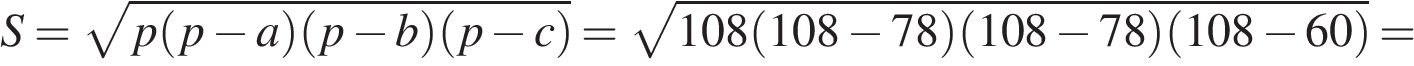
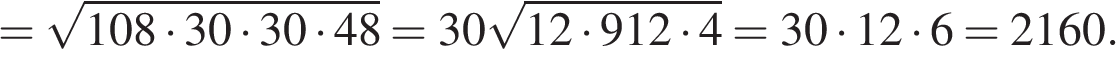
Трапеция
1.
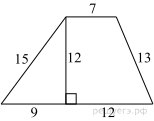 Найдите площадь трапеции, изображённой на рисунке.
Найдите площадь трапеции, изображённой на рисунке.
Решение.
Площадь трапеции равна произведению полусуммы оснований на высоту:
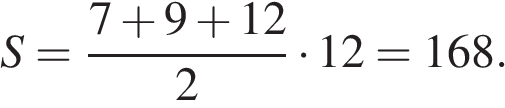
Ответ: 168.
2.
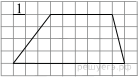 Найдите площадь трапеции, изображённой на рисунке.
Найдите площадь трапеции, изображённой на рисунке.
Решение.
Площадь трапеции равна произведению полусуммы оснований на высоту:
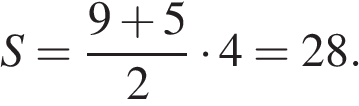
Ответ: 28.
3.
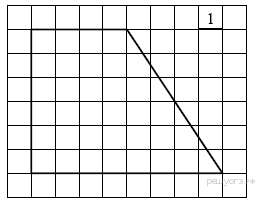 Найдите площадь трапеции, изображённой на рисунке.
Найдите площадь трапеции, изображённой на рисунке.
Решение.
Площадь трапеции равна произведению полусуммы оснований на высоту:
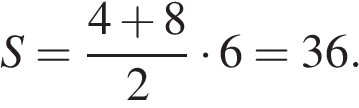
Ответ: 36
4.
Основания трапеции равны 18 и 12, одна из боковых сторон равна  , а угол между ней и одним из оснований равен 135°. Найдите площадь трапеции.
, а угол между ней и одним из оснований равен 135°. Найдите площадь трапеции.
Решение.
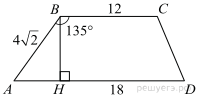
Пусть дана трапеция ABCD, где AD = 18, BC = 12, AB =  , а ∠ABC = 135°. Опустим перпендикуляр BH на сторону AD. Угол ABHравен: 135° − 90° = 45°. Таким образом, треугольник ABH является прямоугольным и равнобедренным. Найдем высоту BH:
, а ∠ABC = 135°. Опустим перпендикуляр BH на сторону AD. Угол ABHравен: 135° − 90° = 45°. Таким образом, треугольник ABH является прямоугольным и равнобедренным. Найдем высоту BH:
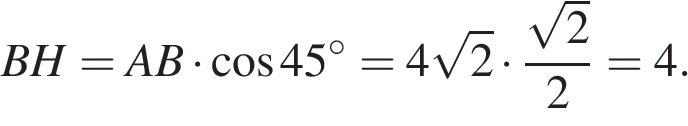
Площадь трапеции равна произведению полусумму оснований на высоту:
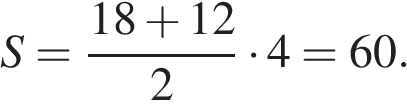
Ответ: 60.
5.
Основания трапеции равны 18 и 12, одна из боковых сторон равна 6, а синус угла между ней и одним из оснований равен 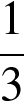 . Найдите площадь трапеции.
. Найдите площадь трапеции.
Решение.
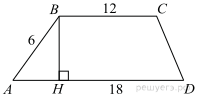
Пусть дана трапеция ABCD, где AD = 18, BC = 12, AB = 6, а 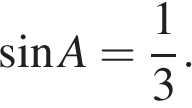 Опустим перпендикуляр BH на сторону AD. Найдем высоту BH:
Опустим перпендикуляр BH на сторону AD. Найдем высоту BH:
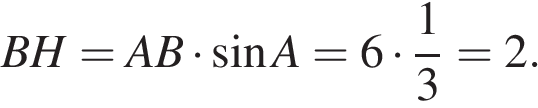
Площадь трапеции равна полусумме оснований на высоту:
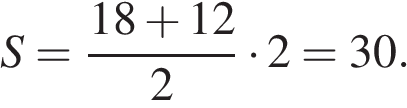
Ответ: 30.
6.
Основания трапеции равны 18 и 12, одна из боковых сторон равна 6, а косинус угла между ней и одним из оснований равен 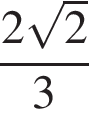 . Найдите площадь трапеции.
. Найдите площадь трапеции.
Решение.
Пусть дана трапеция ABCD, где AD = 18, BC = 12, AB = 6, а 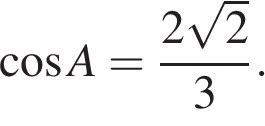 Опустим перпендикуляр BH на сторону AD. Найдем синус угла из основного тригонометрического тождества:
Опустим перпендикуляр BH на сторону AD. Найдем синус угла из основного тригонометрического тождества:
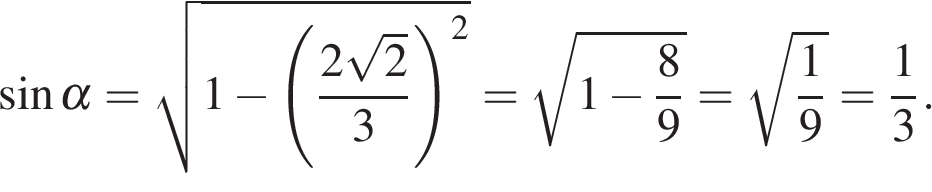
Найдем высоту BH:
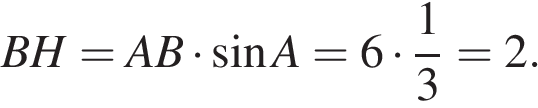
Площадь трапеции равна полусумме оснований на высоту:
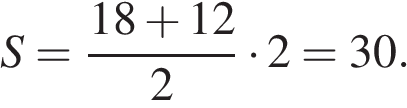
Ответ: 30.
7.
Основания трапеции равны 18 и 12, одна из боковых сторон равна 6, а тангенс угла между ней и одним из оснований равен 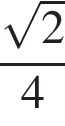 . Найдите площадь трапеции.
. Найдите площадь трапеции.
Решение.
Пусть дана трапеция ABCD, где AD = 18, BC = 12, AB = 6, а 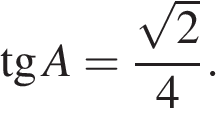 Опустим перпендикуляр BH на сторону AD. Найдем синус угла. В прямоугольном треугольнике тангенс определяется как отношение противолежащего катета к прилежащему. Имеем:
Опустим перпендикуляр BH на сторону AD. Найдем синус угла. В прямоугольном треугольнике тангенс определяется как отношение противолежащего катета к прилежащему. Имеем:
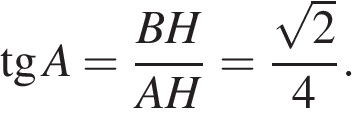
Таким образом, 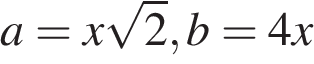 , где x — число.
, где x — число.
По теореме Пифагора гипотенуза этого прямоугольного треугольника равна:
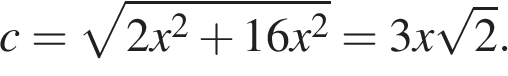
.
В прямоугольном треугольнике синус определяется как отношение противолежащего катета к гипотенузе. Имеем:
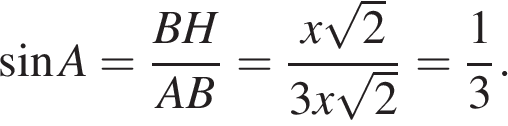
Найдем высоту BH:
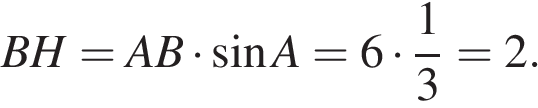
Площадь трапеции равна полусумме оснований на высоту:
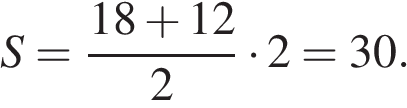
Ответ: 30.
8.
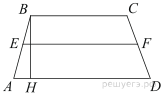
Средняя линия трапеции равна 11, а меньшее основание равно 5. Найдите большее основание трапеции.
Решение.
↓Средняя линия трапеции равна полусумме оснований. Имеем:
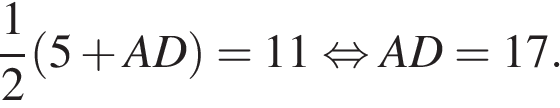
Ответ: 17.
9.
 Найдите площадь трапеции, изображённой на рисунке.
Найдите площадь трапеции, изображённой на рисунке.
Решение.
По формуле площади трапеции имеем:
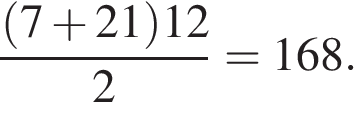
Ответ: 168.
10.
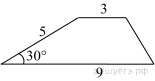
Боковая сторона трапеции равна 5, а один из прилегающих к ней углов равен 30°. Найдите площадь трапеции, если её основания равны 3 и 9.
Решение.
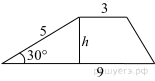
Площадь трапеции вычисляется по формуле
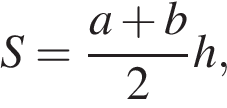 где
где 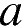 и
и 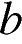 — основания, а
— основания, а 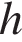 — высота трапеции. Найдём высоту:
— высота трапеции. Найдём высоту: 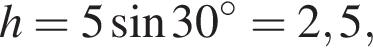 следовательно,
следовательно, 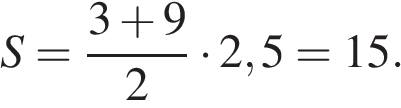
Ответ: 15.
11.
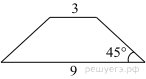
В равнобедренной трапеции основания равны 3 и 9, а один из углов между боковой стороной и основанием равен 45°. Найдите площадь трапеции.
Решение.
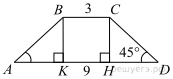
Введём обозначения, как показано на рисунке. Тогда 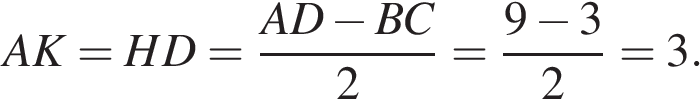 Треугольник
Треугольник  прямоугольный и равнобедренный, тогда высота
прямоугольный и равнобедренный, тогда высота 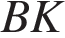 равна 3. Откуда
равна 3. Откуда 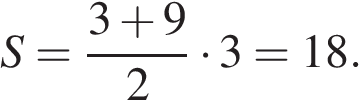
Ответ: 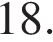
12.
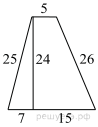
Найдите площадь трапеции, изображённой на рисунке.
Решение.
Площадь трапеции вычисляется по формуле 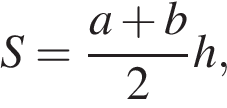 где
где 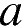 и
и 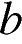 — основания, а
— основания, а 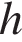 — высота трапеции.
— высота трапеции.
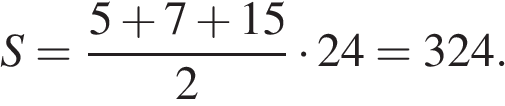
Ответ: 324.
13.
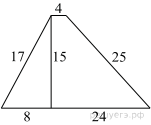
Найдите площадь трапеции, изображённой на рисунке.
Решение.
Площадь трапеции вычисляется по формуле 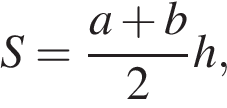 где
где 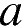 и
и 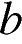 — основания, а
— основания, а 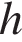 — высота трапеции.
— высота трапеции.
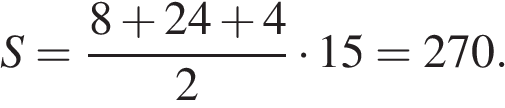
Ответ: 270.
14.
Основания равнобедренной трапеции равны 5 и 17, а ее боковые стороны равны 10. Найдите площадь трапеции.
Решение.
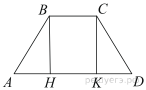
Проведём высоты в трапеции и введём обозначения как показано на рисунке. В четырёхугольнике 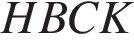
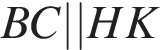 и
и 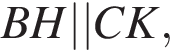 следовательно, он параллелограмм. Угол
следовательно, он параллелограмм. Угол 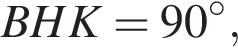 значит,
значит, 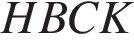 — прямоугольник, откуда
— прямоугольник, откуда  и
и 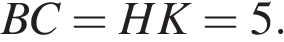 Поскольку трапеция равнобедренная, углы
Поскольку трапеция равнобедренная, углы  и
и  равны. Треугольники
равны. Треугольники  и
и  прямоугольные,
прямоугольные, 
 следовательно, эти треугольники равны, откуда
следовательно, эти треугольники равны, откуда 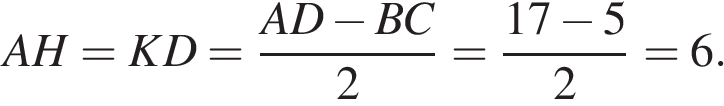 Из треугольника
Из треугольника 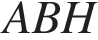 по теореме Пифагора найдём высоту
по теореме Пифагора найдём высоту 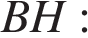
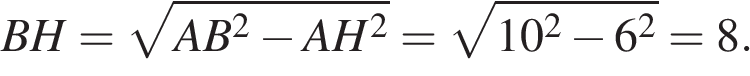
Найдём площадь трапеции:
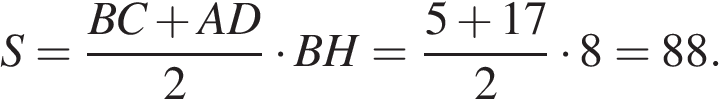
Ответ: 88.
15.
 Основания трапеции равны 7 и 49, одна из боковых сторон равна 18 , а косинус угла между ней и одним из оснований равен
Основания трапеции равны 7 и 49, одна из боковых сторон равна 18 , а косинус угла между ней и одним из оснований равен 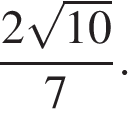 Найдите площадь трапеции.
Найдите площадь трапеции.
Решение.
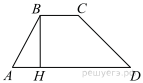 Проведём высоту и введём обозначения как показано на рисунке. Пусть сторона
Проведём высоту и введём обозначения как показано на рисунке. Пусть сторона  тогда
тогда 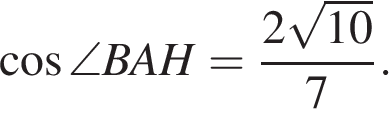 Из прямоугольного треугольника
Из прямоугольного треугольника 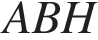 найдём высоту
найдём высоту 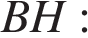
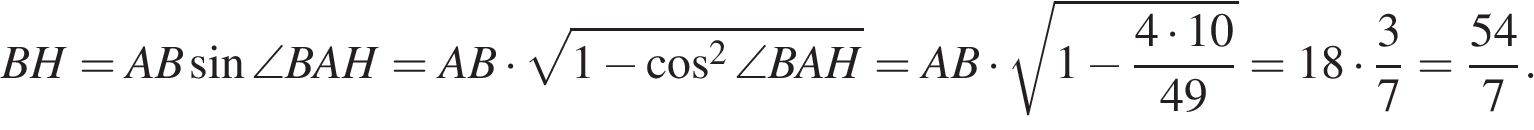
Найдём площадь трапеции как произведение полусуммы оснований на высоту:
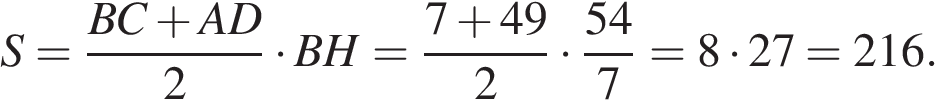
Ответ: 216.
16.
 Основания трапеции равны 1 и 13, одна из боковых сторон равна
Основания трапеции равны 1 и 13, одна из боковых сторон равна  , а угол между ней и одним из оснований равен 135°. Найдите площадь трапеции.
, а угол между ней и одним из оснований равен 135°. Найдите площадь трапеции.
Решение.
 Проведём построения и введём обозначения как показано на рисунке. Отрезок
Проведём построения и введём обозначения как показано на рисунке. Отрезок  — высота. Пусть угол
— высота. Пусть угол  равен 135°. Сумма смежных углов трапеции, прилежащих к боковой стороне равна 180°, поэтому величина угла
равен 135°. Сумма смежных углов трапеции, прилежащих к боковой стороне равна 180°, поэтому величина угла  равна 180° − 135° = 45°. Из прямоугольного треугольника
равна 180° − 135° = 45°. Из прямоугольного треугольника  найдём высоту
найдём высоту 
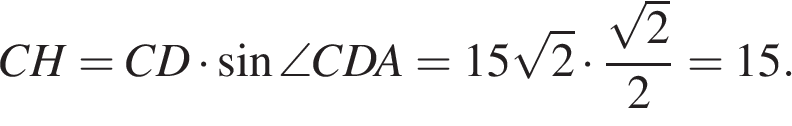
Площадь трапеции равна произведению полусуммы оснований на высоту:
Ответ: 105.
Примечание.
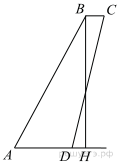 В данном задании открытого банка приведён некорректный рисунок. Заметим, что
В данном задании открытого банка приведён некорректный рисунок. Заметим, что  в то время как полная длина
в то время как полная длина  равна 13. Следовательно, трапеция выглядит как показано на рисунке справа и в таком случае более корректно было бы говорить, что нужно искать
равна 13. Следовательно, трапеция выглядит как показано на рисунке справа и в таком случае более корректно было бы говорить, что нужно искать  а не
а не  Впрочем, ответ задачи от этого не изменяется.
Впрочем, ответ задачи от этого не изменяется.
17.
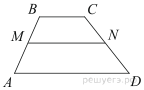
В трапеции ABCD AD = 5, BC = 2, а её площадь равна 28. Найдите площадь трапеции BCNM, где MN – средняя линия трапеции ABCD.
Решение.
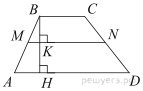
Проведём высоту 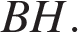 Средняя линия равна полусумме оснований:
Средняя линия равна полусумме оснований: 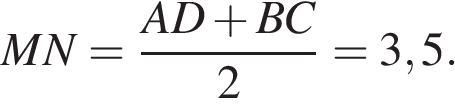 Площадь трапеции равна произведению полусуммы оснований на высоту:
Площадь трапеции равна произведению полусуммы оснований на высоту:
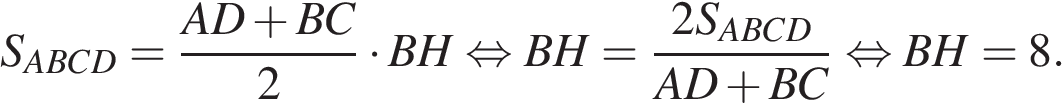
Поскольку 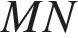 — средняя линия,
— средняя линия, 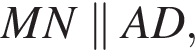 поэтому
поэтому  Отрезки
Отрезки  и
и 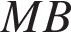 равны,
равны, 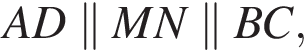 по теореме Фалеса получаем, что
по теореме Фалеса получаем, что 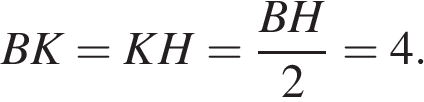 Найдём площадь трапеции
Найдём площадь трапеции 
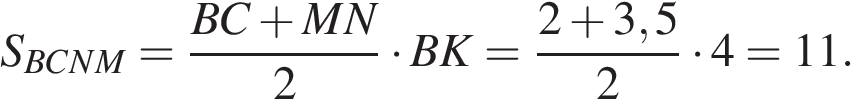
Ответ: 11.
18.
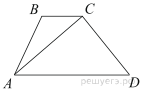
В трапеции ABCD AD = 3, BC = 1, а её площадь равна 12. Найдите площадь треугольника ABC.
Решение.
Пусть длина высоты трапеции равна 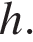 Площадь трапеции можно найти как произведение полусуммы оснований на высоту:
Площадь трапеции можно найти как произведение полусуммы оснований на высоту:
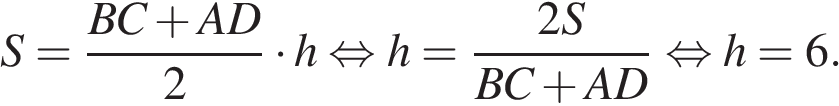
Высота трапеции также является высотой треугольника  Найдём площадь треугольника
Найдём площадь треугольника 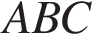 как полупроизведение основания на высоту:
как полупроизведение основания на высоту:
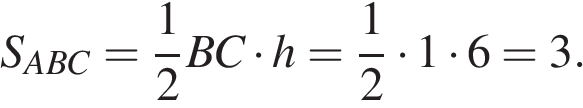
Ответ: 3.
19.
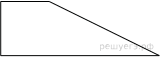
Тангенс острого угла прямоугольной трапеции равен 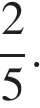 Найдите её большее основание, если меньшее основание равно высоте и равно 58.
Найдите её большее основание, если меньшее основание равно высоте и равно 58.
Решение.
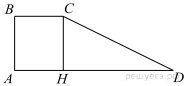
Проведём высоту и введём обозначения как показано на рисунке.
По условию: BC = CH = AH = 58.
Треугольник HCD прямоугольный, следовательно:
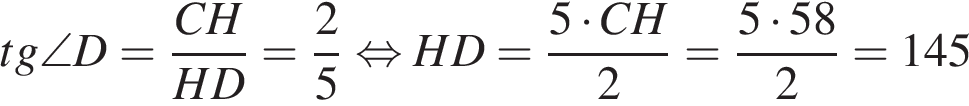 .
.
Таким образом, 
Ответ: 203.
20.
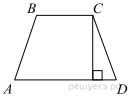
Высота равнобедренной трапеции, проведённая из вершины C, делит основание AD на отрезки длиной 2 и 9. Найдите длину основания BC.
Решение.
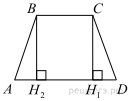
Проведем высоту BH2.
Так как данная трапеция равнобедренная, отрезки 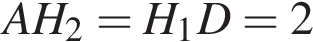 .
.
Заметим, что 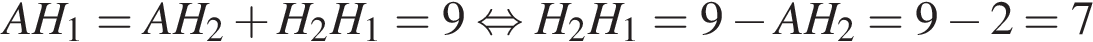 , а так как BC и H1H2 параллельны, а BH2 и CH1 перпендикулярны к BC, то BC = H2H1 = 7.
, а так как BC и H1H2 параллельны, а BH2 и CH1 перпендикулярны к BC, то BC = H2H1 = 7.
Ответ: 7.
21.
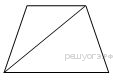
Основания равнобедренной трапеции равны 4 и 14, боковая сторона равна 13. Найдите длину диагонали трапеции.
Решение.
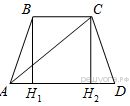
Проведём высоту и введём обозначения как показано на рисунке.
Отрезок H1H2 = BC = 4, а отрезки 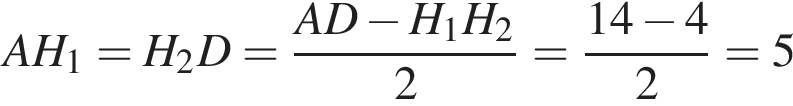 , так как трапеция равнобедренная.
, так как трапеция равнобедренная.
По теореме Пифагора найдем сторону CH2 в треугольнике CDH2:
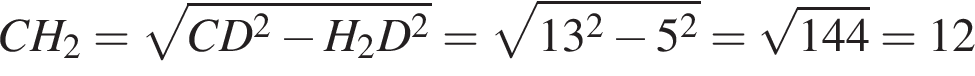
Теперь, найдем AC (диагональ трапеции) из треугольника ACH2:
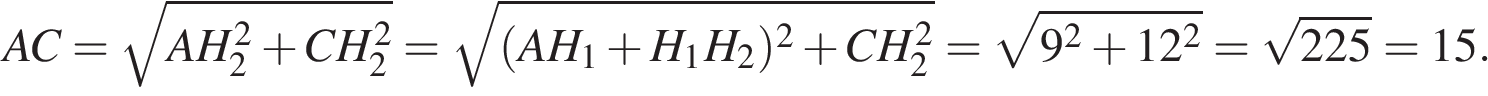
Ответ: 15.
22.
Основания трапеции равны 9 и 54, одна из боковых сторон равна 27, а косинус угла между ней и одним из оснований равен 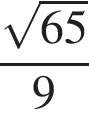 . Найдите площадь трапеции.
. Найдите площадь трапеции.
Решение.
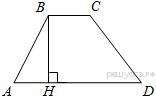
Пусть дана трапеция ABCD, где AD = 54, BC = 9, AB = 27, а 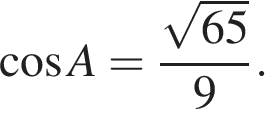 Опустим перпендикуляр BH на сторону AD. Найдем синус угла из основного тригонометрического тождества:
Опустим перпендикуляр BH на сторону AD. Найдем синус угла из основного тригонометрического тождества:
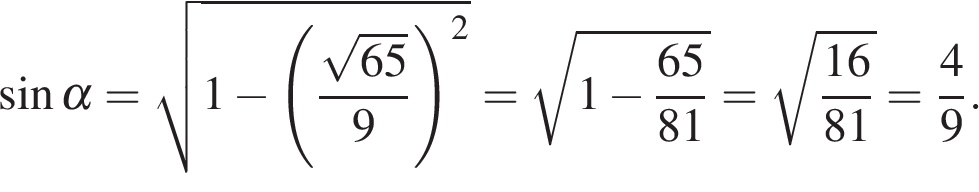
Найдем высоту BH:
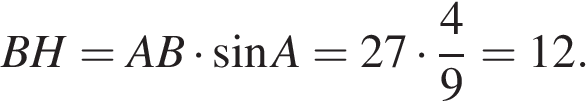
Площадь трапеции равна полусумме оснований на высоту:
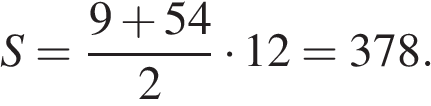
Ответ: 378.
23.

В трапеции ABCD известно, что AD = 6, BC = 2, а её площадь равна 32. Найдите площадь трапеции BCNM, где MN – средняя линия трапеции ABCD.
Решение.

Проведём высоту 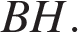 Средняя линия равна полусумме оснований:
Средняя линия равна полусумме оснований: 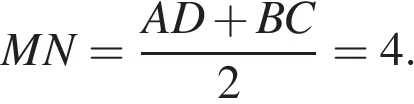 Площадь трапеции равна произведению полусуммы оснований на высоту:
Площадь трапеции равна произведению полусуммы оснований на высоту:
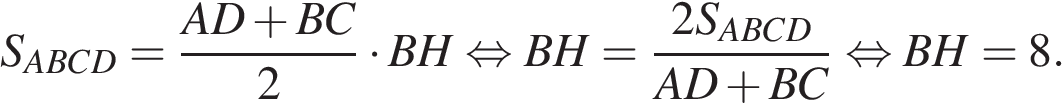
Поскольку  — средняя линия,
— средняя линия, 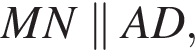 поэтому
поэтому  Отрезки
Отрезки  и
и 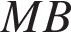 равны,
равны, 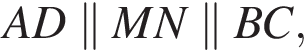 по теореме Фаллеса получаем, что
по теореме Фаллеса получаем, что 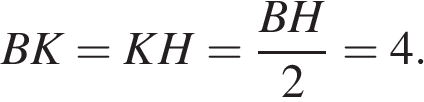 Найдём площадь трапеции
Найдём площадь трапеции 
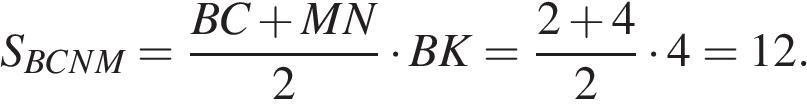
Ответ: 12.
24.
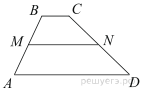
В трапеции ABCD известно, что AD = 5, BC = 1, а её площадь равна 51. Найдите площадь трапеции BCNM, где MN – средняя линия трапеции ABCD.
Решение.
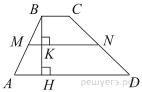
Проведём высоту  Средняя линия равна полусумме оснований:
Средняя линия равна полусумме оснований: 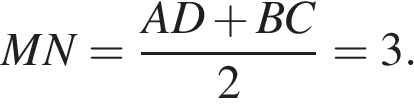 Площадь трапеции равна произведению полусуммы оснований на высоту:
Площадь трапеции равна произведению полусуммы оснований на высоту:
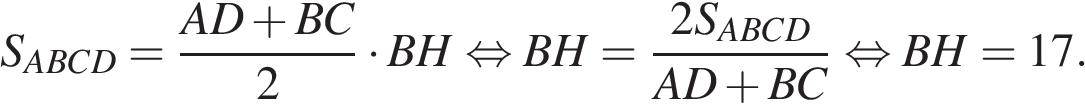
Поскольку  — средняя линия,
— средняя линия,  поэтому
поэтому  Отрезки
Отрезки  и
и 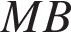 равны,
равны, 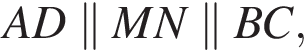 по теореме Фаллеса получаем, что
по теореме Фаллеса получаем, что 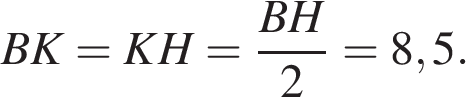 Найдём площадь трапеции
Найдём площадь трапеции 
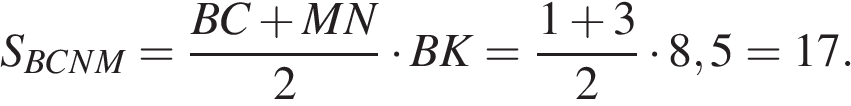
Ответ: 17.
25.

В трапеции ABCD известно, что AD = 8, BC = 5, а её площадь равна 52. Найдите площадь трапеции BCNM, где MN – средняя линия трапеции ABCD.
Решение.

Проведём высоту 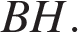 Средняя линия равна полусумме оснований:
Средняя линия равна полусумме оснований: 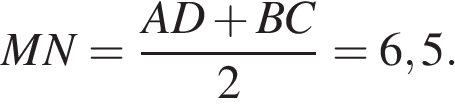 Площадь трапеции равна произведению полусуммы оснований на высоту:
Площадь трапеции равна произведению полусуммы оснований на высоту:
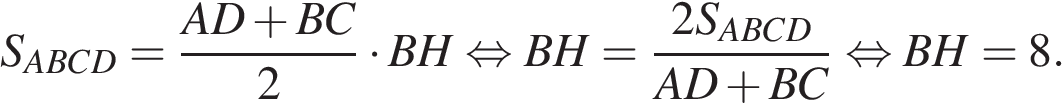
Поскольку  — средняя линия,
— средняя линия, 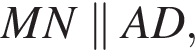 поэтому
поэтому  Отрезки
Отрезки  и
и 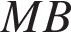 равны,
равны, 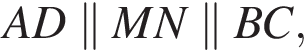 по теореме Фаллеса получаем, что
по теореме Фаллеса получаем, что 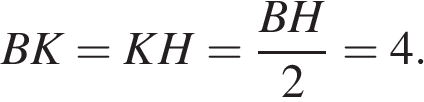 Найдём площадь трапеции
Найдём площадь трапеции 
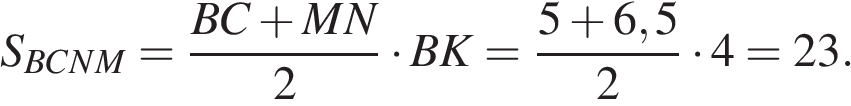
Ответ: 23.
26.

В трапеции ABCD известно, что AD = 2, BC = 1, а её площадь равна 48. Найдите площадь трапеции BCNM, где MN – средняя линия трапеции ABCD.
Решение.

Проведём высоту 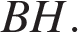 Средняя линия равна полусумме оснований:
Средняя линия равна полусумме оснований: 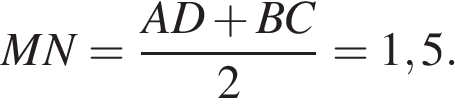 Площадь трапеции равна произведению полусуммы оснований на высоту:
Площадь трапеции равна произведению полусуммы оснований на высоту:
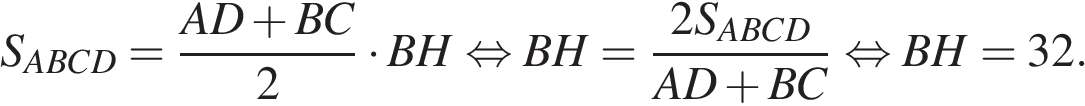
Поскольку 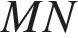 — средняя линия,
— средняя линия, 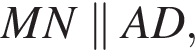 поэтому
поэтому  Отрезки
Отрезки  и
и 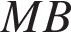 равны,
равны, 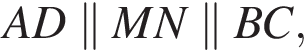 по теореме Фаллеса получаем, что
по теореме Фаллеса получаем, что 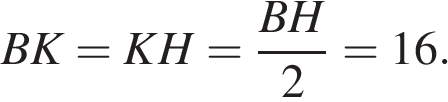 Найдём площадь трапеции
Найдём площадь трапеции 
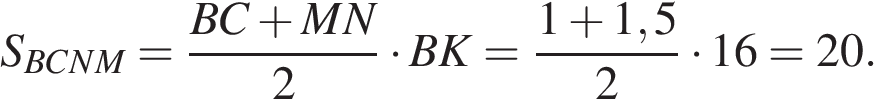
Ответ: 20.
27.

В трапеции ABCD известно, что AD = 7, BC = 5, а её площадь равна 72. Найдите площадь трапеции BCNM, где MN – средняя линия трапеции ABCD.
Решение.

Проведём высоту  Средняя линия равна полусумме оснований:
Средняя линия равна полусумме оснований: 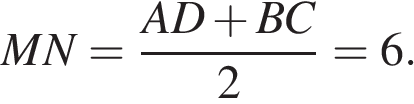 Площадь трапеции равна произведению полусуммы оснований на высоту:
Площадь трапеции равна произведению полусуммы оснований на высоту:
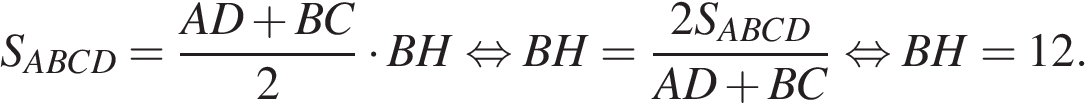
Поскольку 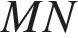 — средняя линия,
— средняя линия, 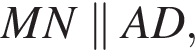 поэтому
поэтому  Отрезки
Отрезки  и
и 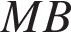 равны,
равны, 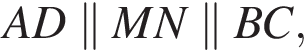 по теореме Фалеса получаем, что
по теореме Фалеса получаем, что 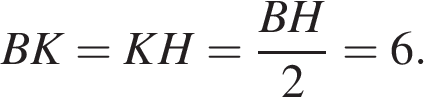 Найдём площадь трапеции
Найдём площадь трапеции 
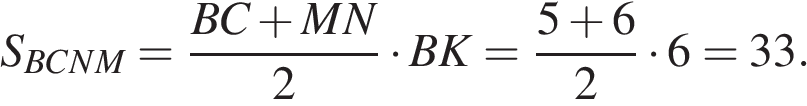
Ответ: 33.
28.
Основания трапеции равны 6 и 24, одна из боковых сторон равна 11, а синус угла между ней и одним из оснований равен  . Найдите площадь трапеции.
. Найдите площадь трапеции.
Решение.
Пусть дана трапеция ABCD, где AD = 24, BC = 6, AB = 11, а 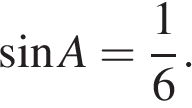 Опустим перпендикуляр BH на сторону AD. Найдем высоту BH:
Опустим перпендикуляр BH на сторону AD. Найдем высоту BH:
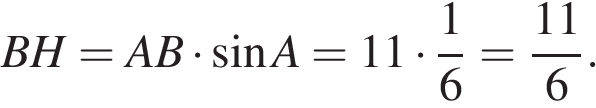
Площадь трапеции равна полусумме оснований на высоту:
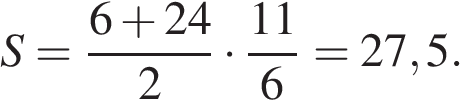
Ответ: 27,5.
29.

В трапеции ABCD известно, что AD = 5, BC = 1, а её площадь равна 12. Найдите площадь трапеции BCNM, где MN – средняя линия трапеции ABCD.
Решение.

Проведём высоту  Средняя линия равна полусумме оснований:
Средняя линия равна полусумме оснований:  Площадь трапеции равна произведению полусуммы оснований на высоту:
Площадь трапеции равна произведению полусуммы оснований на высоту:

Поскольку  — средняя линия,
— средняя линия,  поэтому
поэтому  Отрезки
Отрезки  и
и  равны,
равны,  по теореме Фаллеса получаем, что
по теореме Фаллеса получаем, что  Найдём площадь трапеции
Найдём площадь трапеции 

Ответ: 4.
30.
Основания трапеции равны 7 и 63, одна из боковых сторон равна 18, а косинус угла между ней и одним из оснований равен 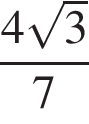 . Найдите площадь трапеции.
. Найдите площадь трапеции.
Решение.
Пусть дана трапеция ABCD, где AD = 63, BC = 7, AB = 18, а 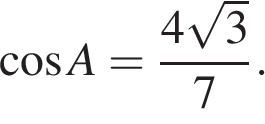 Опустим перпендикуляр BH на сторону AD. Найдем синус угла из основного тригонометрического тождества:
Опустим перпендикуляр BH на сторону AD. Найдем синус угла из основного тригонометрического тождества:
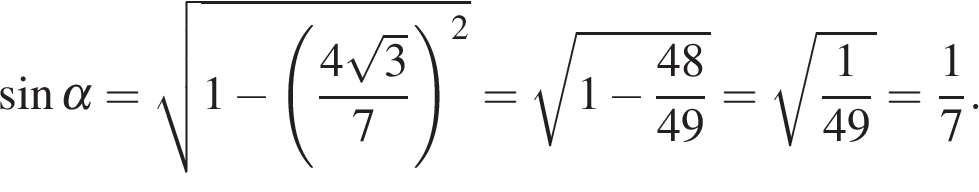
Найдем высоту BH:
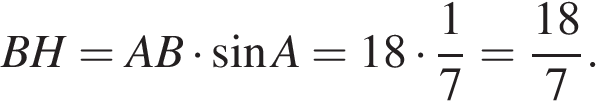
Площадь трапеции равна полусумме оснований на высоту:
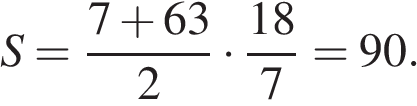
Ответ: 90.
31.
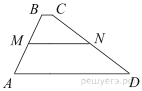
В трапеции ABCD известно, что AD = 9, BC = 1, а её площадь равна 70. Найдите площадь трапеции BCNM, где MN – средняя линия трапеции ABCD.
Решение.
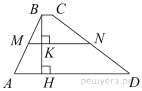
Проведём высоту 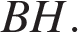 Средняя линия равна полусумме оснований:
Средняя линия равна полусумме оснований: 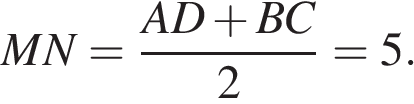 Площадь трапеции равна произведению полусуммы оснований на высоту:
Площадь трапеции равна произведению полусуммы оснований на высоту:
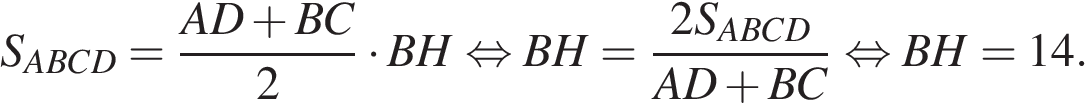
Поскольку 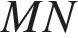 — средняя линия,
— средняя линия, 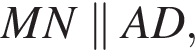 поэтому
поэтому  Отрезки
Отрезки  и
и 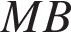 равны,
равны, 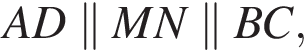 по теореме Фаллеса получаем, что
по теореме Фаллеса получаем, что 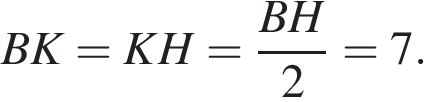 Найдём площадь трапеции
Найдём площадь трапеции 
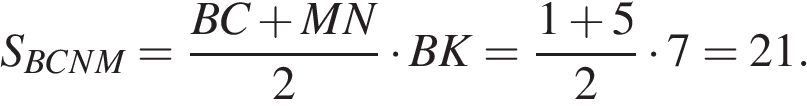
Ответ: 21.
32.
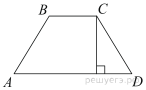
Высота равнобедренной трапеции, проведённая из вершины  , отсекает от основания
, отсекает от основания  отрезок длиной 2. Длина основания
отрезок длиной 2. Длина основания 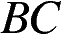 равна 7. Найдите длину основания
равна 7. Найдите длину основания  .
.
Решение.
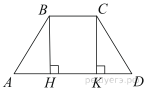
Проведём вторую высоту и введём обозначения как показано на рисунке. Рассмотрим треугольники 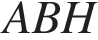 и
и  они прямоугольные,
они прямоугольные, 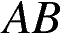 равно
равно 
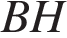 равно
равно  следовательно, эти треугольники равны, откуда
следовательно, эти треугольники равны, откуда  Найдём отрезок
Найдём отрезок 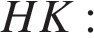
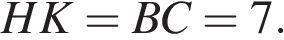 Таким образом,
Таким образом, 
Ответ: 11.
Треугольники общего вида
1.
В треугольнике одна из сторон равна 10, а опущенная на нее высота — 5. Найдите площадь треугольника.
Решение.
Площадь треугольника равна половине произведения высоты на основание. Таким образом:
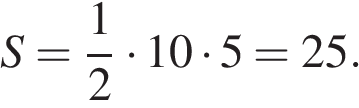
Ответ: 25.
2.
В треугольнике одна из сторон равна 10, другая равна  , а угол между ними равен 60°. Найдите площадь треугольника.
, а угол между ними равен 60°. Найдите площадь треугольника.
Решение.
Площадь треугольника равна половине произведения сторон на синус угла между ними. Имеем:
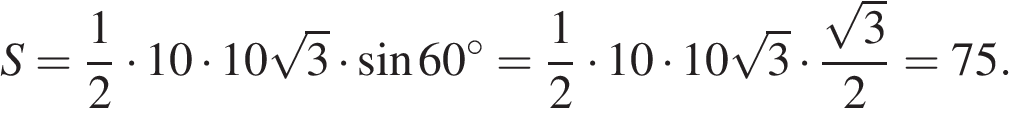
Ответ: 75.
3.
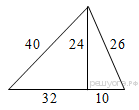 Найдите площадь треугольника, изображённого на рисунке.
Найдите площадь треугольника, изображённого на рисунке.
Решение.
Заметим, что треугольник со сторонами 24, 32 и 40 подобен египетскому треугольнику со сторонами 3, 4, 5 с коэффициентом 8. Следовательно, этот треугольник прямоугольный, а отрезок длины 24 — высота изображенного на рисунке треугольника. Тогда его площадь можно найти как половину произведения основания на высоту:
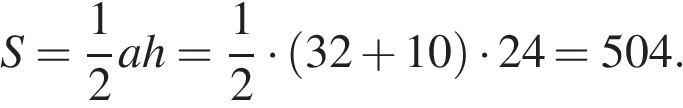
Ответ: 504.
4.
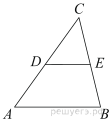
В треугольнике ABC отрезок DE — средняя линия. Площадь треугольника CDE равна 97. Найдите площадь треугольника ABC.
Решение.
Треугольники ABC и DEC подобны по двум углам. Коэффициент подобия k = 2. Значит 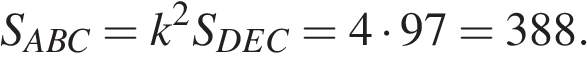
Ответ: 388.
5.
Сторона треугольника равна 12, а высота, проведённая к этой стороне, равна 33. Найдите площадь этого треугольника.
Решение.
Площадь треугольника равна полупроизведению стороны треугольника на высоту, проведенную к этой стороне:
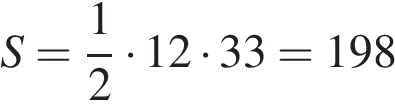
Ответ: 198
Параллелограмм
1.
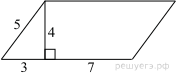 Найдите площадь параллелограмма, изображённого на рисунке.
Найдите площадь параллелограмма, изображённого на рисунке.
Решение.
Площадь параллелограмма равна произведению длины основания на высоту:
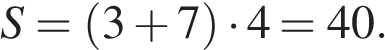
Ответ: 40.
2.
Сторона ромба равна 5, а диагональ равна 6. Найдите площадь ромба.
Решение.
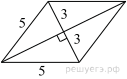
Диагонали ромба пересекаются под углом 90° и точкой пересечения делятся пополам. Из прямоугольного треугольника, катетами которого являются половины диагоналей ромба, а гипотенузой — сторона ромба, по теореме Пифагора найдем половину неизвестной диагонали: 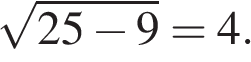 Тогда вся неизвестная диагональ равна 8.
Тогда вся неизвестная диагональ равна 8.
Площадь ромба равна половине произведения диагоналей:
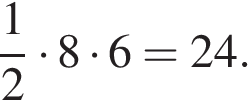
Ответ: 24.
3.
Периметр ромба равен 40, а один из углов равен 30°. Найдите площадь ромба.
Решение.
Периметр ромба равен сумме длин всех его сторон. Так как все стороны равны, сторона ромба равна 10. Площадь ромба равна произведению сторон на синус угла между ними. Таким образом,
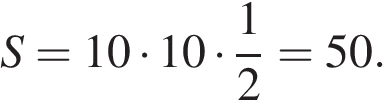
Ответ: 50.
4.
Периметр ромба равен 24, а синус одного из углов равен 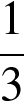 . Найдите площадь ромба.
. Найдите площадь ромба.
Решение.
Периметр ромба равен сумме длин всех его сторон. Так как все стороны равны, сторона ромба равна 6. Площадь ромба равна произведению сторон на синус угла между ними, поэтому
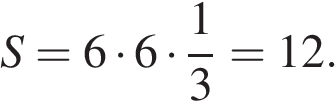
Ответ: 12.
5.
Одна из сторон параллелограмма равна 12, а опущенная на нее высота равна 10. Найдите площадь параллелограмма.
Решение.
Площадь параллелограмма равна произведению высоты на основание. Таким образом,
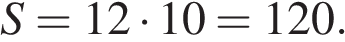
Ответ: 120.
6.
Одна из сторон параллелограмма равна 12, другая равна 5, а один из углов — 45°. Найдите площадь параллелограмма, делённую на 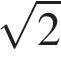 .
.
Решение.
Площадь параллелограмма равна произведению сторон на синус угла между ними:

Ответ: 30.
7.
Одна из сторон параллелограмма равна 12, другая равна 5, а синус одного из углов равен 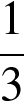 . Найдите площадь параллелограмма.
. Найдите площадь параллелограмма.
Решение.
Площадь параллелограмма равна произведению сторон на синус угла между ними, поэтому
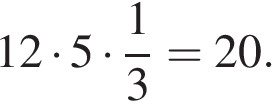
Ответ: 20.
8.
Одна из сторон параллелограмма равна 12, другая равна 5, а косинус одного из углов равен 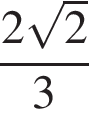 . Найдите площадь параллелограмма.
. Найдите площадь параллелограмма.
Решение.
Площадь параллелограмма равна произведению сторон на синус угла между ними. Cинус угла найдем из основного тригонометрического тождества:
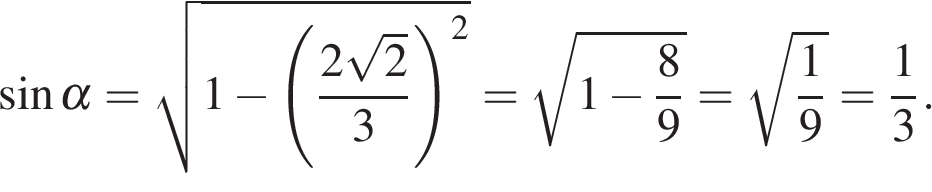
Таким образом,
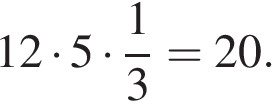
Ответ: 20.
9.
Одна из сторон параллелограмма равна 12, другая равна 5, а тангенс одного из углов равен 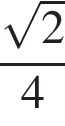 . Найдите площадь параллелограмма.
. Найдите площадь параллелограмма.
Решение.
Площадь параллелограмма равна произведению сторон на синус угла между ними. Найдем синус угла. В прямоугольном треугольнике тангенс определяется как отношение противолежащего катета к прилежащему. Имеем:
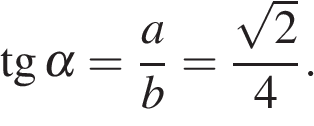
Таким образом, 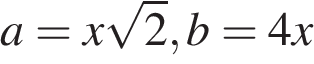 , где x — число.
, где x — число.
По теореме Пифагора гипотенуза этого прямоугольного треугольника равна:
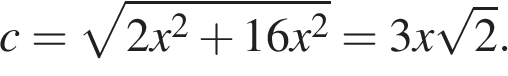
.
В прямоугольном треугольнике синус определяется как отношение противолежащего катета к гипотенузе. Имеем:
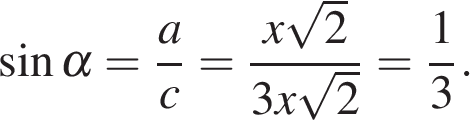
Таким образом,
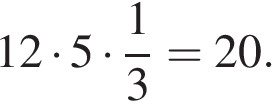
10.
В прямоугольном треугольнике один из катетов равен 10, острый угол, прилежащий к нему, равен 60°, а гипотенуза равна 20. Найдите площадь треугольника, делённую на 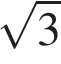 .
.
Решение.
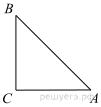
Найдем второй катет треугольника из определения тангенса:
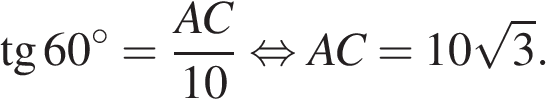
Площадь прямоугольного треугольника равна половине произведения катетов:
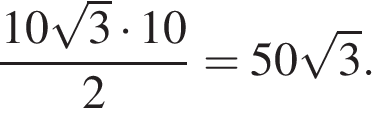
Ответ: 50.
Примечание:
Второй катет можно было найти при помощи теоремы Пифагора.
11.
В ромбе сторона равна 10, одна из диагоналей — 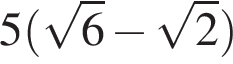 , а угол, лежащий напротив этой диагонали, равен 30°. Найдите площадь ромба.
, а угол, лежащий напротив этой диагонали, равен 30°. Найдите площадь ромба.
Решение.
Площадь ромба равна произведению сторон на синус угла между ними:
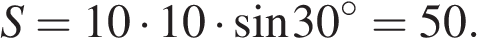
Ответ:50.
Примечание:
Можно найти вторую диагональ по теореме косинусов и вычислить площадь ромба как половина произведения диагоналей.
12.
Радиус круга равен 3, а длина ограничивающей его окружности равна 6π. Найдите площадь круга. В ответ запишите площадь, деленную на π.
Решение.
Площадь круга равна  имеем:
имеем:
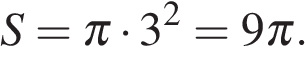
Ответ: 9.
13.
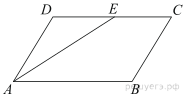
Площадь параллелограмма ABCD равна 56. Точка E — середина стороны CD. Найдите площадь трапеции AECB.
Решение.
Диагональ параллелограмма делит его на два равных треугольника, поэтому  Медиана треугольника делит его на два равновеликих треугольника, поэтому
Медиана треугольника делит его на два равновеликих треугольника, поэтому  Следовательно,
Следовательно,

Ответ: 42.
14.
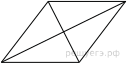 Найдите площадь ромба, если его диагонали равны 14 и 6.
Найдите площадь ромба, если его диагонали равны 14 и 6.
Решение.
Площадь ромба можно найти как половину произведения его диагоналей: 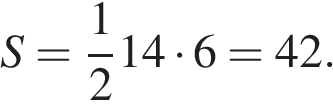
Ответ: 42.
15.
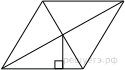 Сторона ромба равна 9, а расстояние от центра ромба до неё равно 1. Найдите площадь ромба.
Сторона ромба равна 9, а расстояние от центра ромба до неё равно 1. Найдите площадь ромба.
Решение.
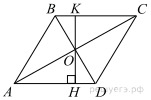 Проведём построение и введём обозначения как показано на рисунке. Учитывая, что
Проведём построение и введём обозначения как показано на рисунке. Учитывая, что  и
и  получаем
получаем  Диагонали ромба точкой пересечения делятся пополам. Рассмотрим треугольники
Диагонали ромба точкой пересечения делятся пополам. Рассмотрим треугольники  и
и  , они прямоугольные,
, они прямоугольные, 
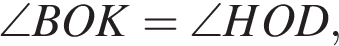 следовательно, треугольники
следовательно, треугольники  и
и  равны, откуда
равны, откуда  то есть высота
то есть высота  Найдём площадь ромба как произведение стороны на высоту:
Найдём площадь ромба как произведение стороны на высоту:

Ответ: 18.
16.
Сторона ромба равна 50, а диагональ равна 80. Найдите площадь ромба.
Решение.
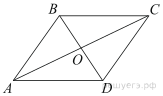
Введём обозначения как показано на рисунке. Диагонали ромба перпендикулярны и делятся точкой пересечения пополам. Пусть 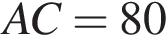 Рассмотрим треугольник
Рассмотрим треугольник 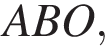 он прямоугольный, из теоремы Пифагора найдём
он прямоугольный, из теоремы Пифагора найдём 
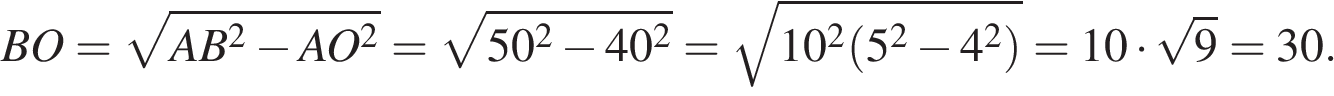
Найдём площадь ромба как половину произведения его диагоналей:
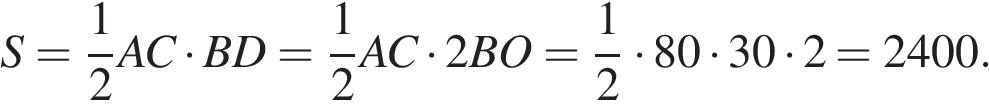
Ответ: 2400.
17.
 Периметр ромба равен 116, а один из углов равен 30°. Найдите площадь ромба.
Периметр ромба равен 116, а один из углов равен 30°. Найдите площадь ромба.
Решение.
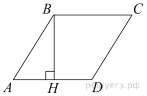 Проведём высоту в ромбе и введём обозначения как показано на рисунке. Все стороны ромба равны, поэтому
Проведём высоту в ромбе и введём обозначения как показано на рисунке. Все стороны ромба равны, поэтому 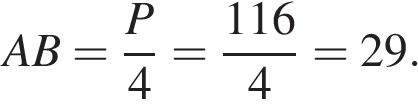 Найдём
Найдём 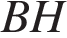 из прямоугольного треугольника
из прямоугольного треугольника 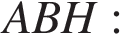
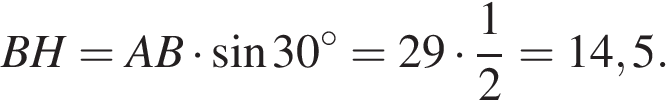
Найдём площадь ромба как произведение стороны на высоту:

Ответ: 420,5.
18.
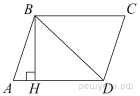
Высота BH параллелограмма ABCD делит его сторону AD на отрезки AH = 1 и HD = 28. Диагональ параллелограмма BD равна 53. Найдите площадь параллелограмма.
Решение.
Из прямоугольного треугольника 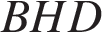 по теореме Пифагора найдём
по теореме Пифагора найдём 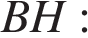
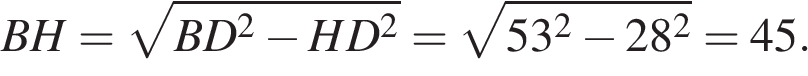
Площадь параллелограмма равна произведению основания на высоту:
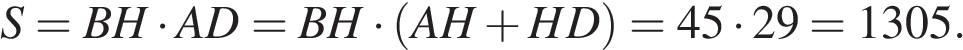
Ответ: 1305.
19.

Высота BH ромба ABCD делит его сторону AD на отрезки AH = 5 и HD = 8. Найдите площадь ромба.
Решение.
Из прямоугольного треугольника 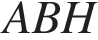 найдём
найдём 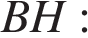
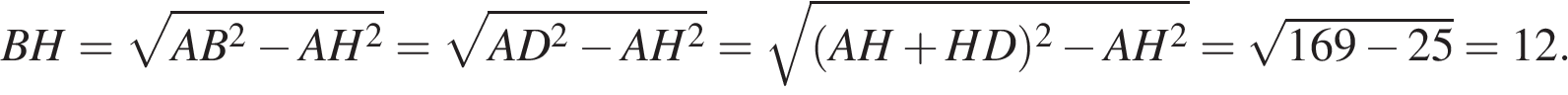
Площадь ромба можно найти как произведение основания на высоту:
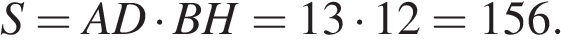
Ответ: 156.
20.
 Площадь ромба равна 54, а периметр равен 36. Найдите высоту ромба.
Площадь ромба равна 54, а периметр равен 36. Найдите высоту ромба.
Решение.
Пусть сторона ромба равна a, тогда
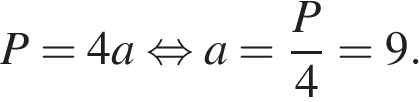
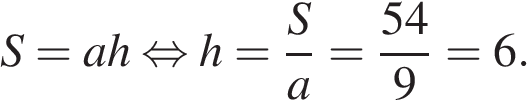
Ответ: 6.
21.
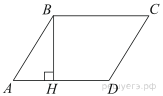
Высота 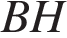 ромба
ромба 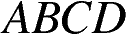 делит его сторону
делит его сторону  на отрезки
на отрезки  и
и  . Найдите площадь ромба.
. Найдите площадь ромба.
Решение.
Из прямоугольного треугольника 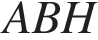 найдём
найдём 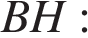
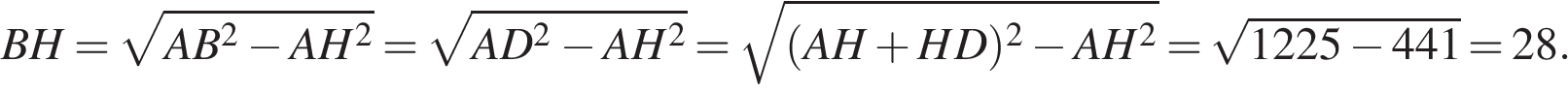
Площадь ромба можно найти как произведение основания на высоту:
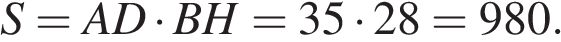
Ответ: 980.






 Периметр квадрата равен 160. Найдите площадь квадрата.
Периметр квадрата равен 160. Найдите площадь квадрата. Найдите площадь квадрата, если его диагональ равна 1.
Найдите площадь квадрата, если его диагональ равна 1. Найдите площадь квадрата, описанного вокруг окружности радиуса 83.
Найдите площадь квадрата, описанного вокруг окружности радиуса 83.
 В прямоугольнике одна сторона равна 96, а диагональ равна 100. Найдите площадь прямоугольника.
В прямоугольнике одна сторона равна 96, а диагональ равна 100. Найдите площадь прямоугольника. В прямоугольном треугольнике гипотенуза равна 70, а один из острых углов равен 45°. Найдите площадь треугольника.
В прямоугольном треугольнике гипотенуза равна 70, а один из острых углов равен 45°. Найдите площадь треугольника.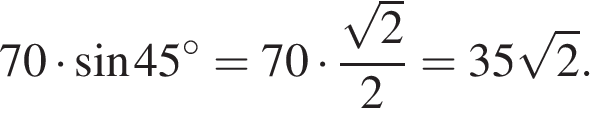 Площадь прямоугольного треугольника можно найти как половину произведения катетов:
Площадь прямоугольного треугольника можно найти как половину произведения катетов: 
 Пусть
Пусть 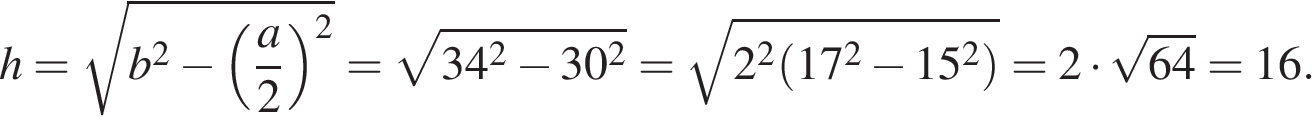
 Периметр равнобедренного треугольника равен 216, а боковая сторона — 78. Найдите площадь треугольника.
Периметр равнобедренного треугольника равен 216, а боковая сторона — 78. Найдите площадь треугольника. Периметр треугольника равен сумме длин его сторон, поэтому длина основания равна 216 − 78 − 78 = 60. Высота
Периметр треугольника равен сумме длин его сторон, поэтому длина основания равна 216 − 78 − 78 = 60. Высота 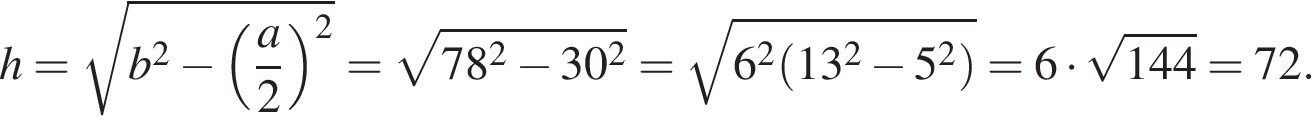
 Найдите площадь трапеции, изображённой на рисунке.
Найдите площадь трапеции, изображённой на рисунке. Найдите площадь трапеции, изображённой на рисунке.
Найдите площадь трапеции, изображённой на рисунке. Найдите площадь трапеции, изображённой на рисунке.
Найдите площадь трапеции, изображённой на рисунке.
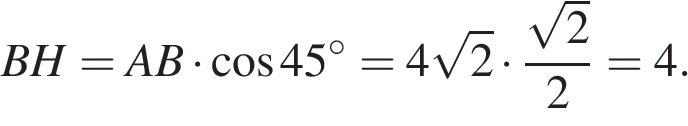

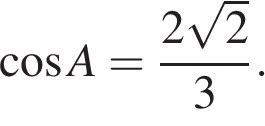 Опустим перпендикуляр BH на сторону AD. Найдем синус угла из основного тригонометрического тождества:
Опустим перпендикуляр BH на сторону AD. Найдем синус угла из основного тригонометрического тождества: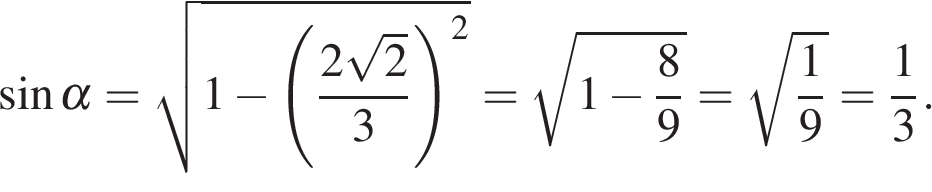
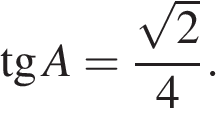 Опустим перпендикуляр BH на сторону AD. Найдем синус угла. В прямоугольном треугольнике тангенс определяется как отношение противолежащего катета к прилежащему. Имеем:
Опустим перпендикуляр BH на сторону AD. Найдем синус угла. В прямоугольном треугольнике тангенс определяется как отношение противолежащего катета к прилежащему. Имеем: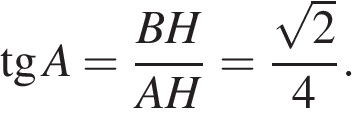
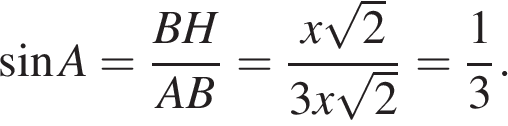









 Основания трапеции равны 7 и 49, одна из боковых сторон равна 18 , а косинус угла между ней и одним из оснований равен
Основания трапеции равны 7 и 49, одна из боковых сторон равна 18 , а косинус угла между ней и одним из оснований равен  Проведём высоту и введём обозначения как показано на рисунке. Пусть сторона
Проведём высоту и введём обозначения как показано на рисунке. Пусть сторона 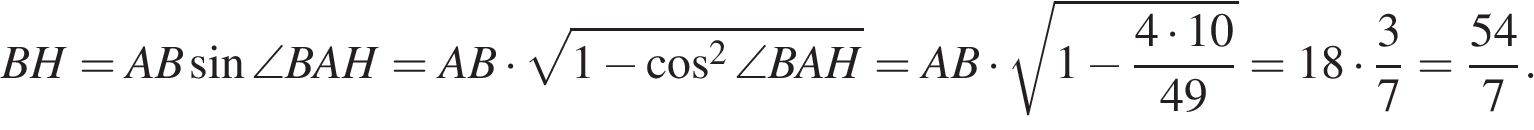
 Проведём построения и введём обозначения как показано на рисунке. Отрезок
Проведём построения и введём обозначения как показано на рисунке. Отрезок 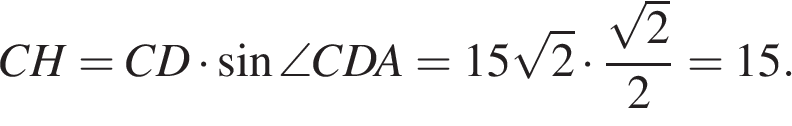
 В данном задании открытого банка приведён некорректный рисунок. Заметим, что
В данном задании открытого банка приведён некорректный рисунок. Заметим, что 










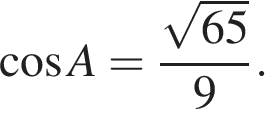 Опустим перпендикуляр BH на сторону AD. Найдем синус угла из основного тригонометрического тождества:
Опустим перпендикуляр BH на сторону AD. Найдем синус угла из основного тригонометрического тождества: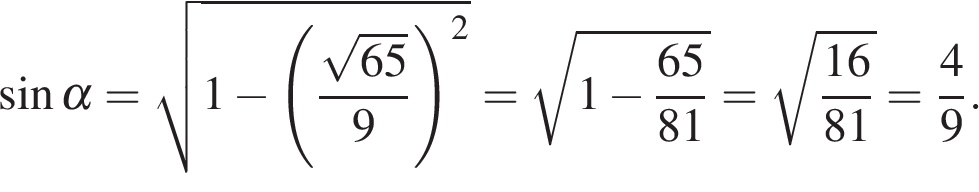


 Средняя линия равна полусумме оснований:
Средняя линия равна полусумме оснований: 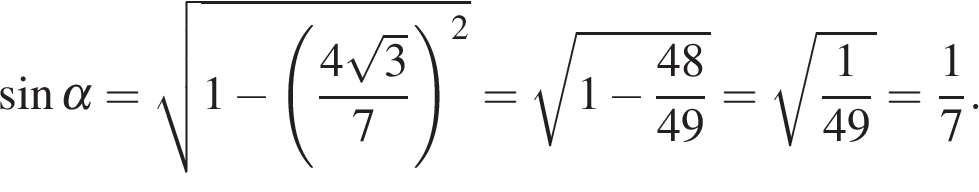




 Найдите площадь треугольника, изображённого на рисунке.
Найдите площадь треугольника, изображённого на рисунке.
 Найдите площадь параллелограмма, изображённого на рисунке.
Найдите площадь параллелограмма, изображённого на рисунке.
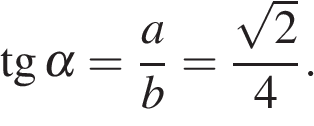
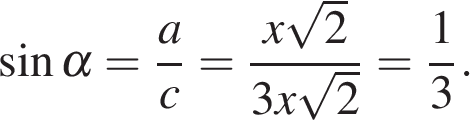


 Найдите площадь ромба, если его диагонали равны 14 и 6.
Найдите площадь ромба, если его диагонали равны 14 и 6. Сторона ромба равна 9, а расстояние от центра ромба до неё равно 1. Найдите площадь ромба.
Сторона ромба равна 9, а расстояние от центра ромба до неё равно 1. Найдите площадь ромба. Проведём построение и введём обозначения как показано на рисунке. Учитывая, что
Проведём построение и введём обозначения как показано на рисунке. Учитывая, что 

 Периметр ромба равен 116, а один из углов равен 30°. Найдите площадь ромба.
Периметр ромба равен 116, а один из углов равен 30°. Найдите площадь ромба. Проведём высоту в ромбе и введём обозначения как показано на рисунке. Все стороны ромба равны, поэтому
Проведём высоту в ромбе и введём обозначения как показано на рисунке. Все стороны ромба равны, поэтому 
 Площадь ромба равна 54, а периметр равен 36. Найдите высоту ромба.
Площадь ромба равна 54, а периметр равен 36. Найдите высоту ромба.










