"Почему по математике тетрадь в клеточку"

Муниципальное бюджетное общеобразовательное учреждение

средняя общеобразовательная школа № 2 г. Нижний Ломов

Дистанционный конкурс «Математика вокруг нас»

«Занимательная математика»

«Почему тетрадь по математике в клеточку?»

Работу выполнила:

ученица 6 «К» класса

МБОУ СОШ №2 г. Нижний Ломов

Царева Дарина

Руководитель:

учитель математики

МБОУ СОШ №2 г. Нижний Ломов

Буренкова Галина Николаевна

г. Нижний Ломов, 2021

Оглавление

Введение. 3

Основная часть. 4

1. Построение на основе свойств фигур 4

2. Вычисление площадей многоугольников 8

3.Формула Пика. 9

4. Построение фигур по заданной площади. 10

5.Игры и задачи на клетчатой бумаге. 11

Заключение: 13

Литература: ……………………………………………………………………………..14

Введение

Тема моего исследования: «Почему тетрадь по математике в клеточку?».

Почему тетрадь по математике в клеточку? Почему именно клетчатая поверхность листа стала настоящей помощницей математики? Что позволяют делать клетки обычной тетради? Каким образом они позволяют совершать ей необыкновенные чудеса?

Цель: узнать, почему тетрадь по математике в клетку.

Задачи:

• отобрать материал для исследования, выбрать главную, интересную, понятную информацию;

• проанализировать и систематизировать полученную информацию;

• найти различные методы и приемы решения задач на клетчатой бумаге;

• создать презентацию по теме исследования;

• сделать выводы по результатам работы.

Гипотеза

Тетрадь в клетку - это важный инструмент в изучении математики.

Методы исследования, использованные в работе:

• 1. Анализ литературы по теме.

• 2.Решение геометрических задач.

• 3. Обобщение материала.

Актуальность проблемы:

Существует много видов тетрадей: в клеточку, в широкую линеечку, косую линеечку. Но на уроках математики мы используем именно тетрадь в клеточку. В ней мы решаем различные задачи и строим геометрические фигуры. Помогает ли клетка при выполнении таких заданий?

Основная часть

Предметом нашего исследования стала обычная тетрадь по математике. Почему именно клетчатая поверхность заполнила её листы? Математика – удивительная наука! И мы рискнули предположить, что клетчатая бумага, обладая волшебными свойствами, помогает ей делать настоящие чудеса.

«На Руси писали на коре деревьев и на вощёных табличках с помощью палочек, сделанных из веток. И только в XIV веке появилась бумага из хлопка и льна. Однако тетради из такой тряпичной бумаги были очень дорогим удовольствием. Они были только у детей состоятельных людей.

Такая бумага, какой мы её знаем сегодня появилась в России только в середине XVI века, но расцвет бумажного производства наступил при Петре Первом. По его указу были построены первые предприятия по производству бумаги под Москвой и Санкт-Петербургом.

Тетради отечественного производства появились в России только в начале XVIII века. Они были настоящими произведениями искусства – с расписной обложкой и водяными знаками на каждой странице. Но тогда тетрадей в клетку не было – только в линейку.

В Советском Союзе у всех школьников были одинаковые тетради – со стандартной неяркой обложкой и текстом гимна с обратной стороны. Сегодня же в магазинах – огромный выбор тетрадей». Так почему же тетрадь по математике в клеточку? Не все ученики, которым мы задавали этот вопрос, сразу же могли дать нам вразумительный ответ. Наверное, она нужна и для того, чтобы удобно было записывать примеры в столбик, и чтобы легче было чертить.

Прежде всего, я решила убедиться, что тетрадь по математике в клеточку, чтобы решать правильно примеры. Провела первый опыт.

Опыт первый:Взяла два листа бумаги: один нелинованный, другой в клеточку. Написала одни и те же примеры на обоих листах. На листе в клеточку примеры получились аккуратно записанными, цифра под нужной цифрой. Все примеры решила без ошибок.

Вывод: На листах в клеточку удобнее записывать обыкновенные и десятичные дроби. Решать примеры со смешанными числами и возводить в степень, приводить к общему знаменателю. Записи получаются аккуратными и занимают меньше места.

Затем я провела второй опыт: на построение геометрических фигур.

Построение геометрических фигур

Опыт второй: Снова взяла два листа бумаги: нелинованный и лист в клеточку. На обоих листах построила одинаковые геометрические фигуры. Оказалось, что на листе бумаги в клеточку чертить легче. Можно быстрее построить по заданным размерам, например, прямоугольник, так как две клеточки это один сантиметр. [2]

Построение геометрических фигур на нелинованном листе бумаги

Построение геометрических фигур на листе бумаги в клеточку

Вывод: Клеточки на бумаге позволяют многие построения проводить только с помощью одной линейки, причём на этой линейке может даже не быть делений.

1. Построение на основе свойств фигур

Тетрадь в клетку очень удобна для занятия геометрией. Она помогает при построении различных геометрических фигур:

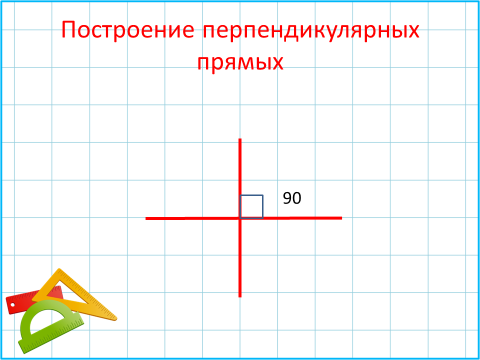
Построение перпендикулярных прямых:Две прямые, образующие при пересечении прямые углы, называют перпендикулярными.  

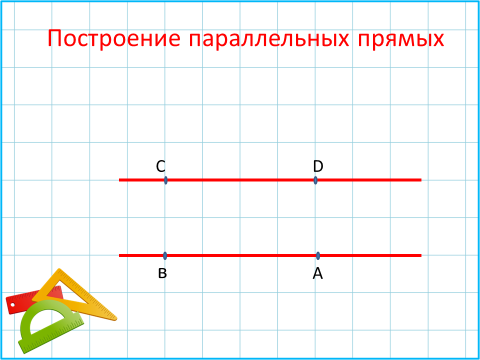
Построение параллельных прямых:Две непересекающиеся прямые на плоскости называют  параллельными. 

И других многоугольников.

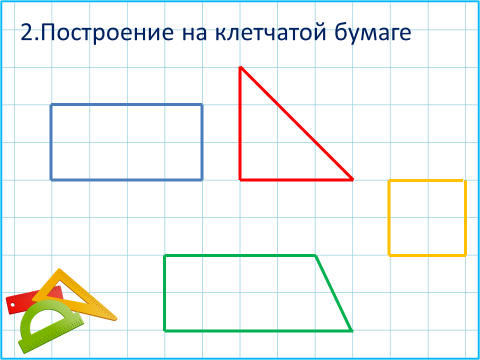
Для построения геометрических фигур нужно помнить их свойства, ведь именно они позволяют использовать клеточки в полной мере.

Построение параллельных прямых, проходящих через два любые узла клетчатой бумаги.

Вывод: тетрадь в клетку помогает при построении геометрических фигур.

Симметрия фигур

В древности слово «симметрия» употреблялось в значении «гармония», «красота». Действительно, в переводе с греческого это слово означает «соразмерность, пропорциональность, одинаковость в расположении частей».

Если мы посмотрим на кленовый лист, снежинку, бабочку. Их объединяет то, что они симметричны. У них есть ось симметрии. Если симметричную фигуру сложить вдоль оси симметрии, то её части совпадут.

У геометрических фигур может быть одна или несколько осей симметрии. В тетради в клетку легко построить симметричные фигуры.

 Задание:

На рис. 1 на клетчатой бумаге изображены фигуры, симметричные относительно изображённой прямой. Нарисуйте на рис. 2 фигуру, симметричную заштрихованной фигуре относительно данной прямой.

1)

Ответ:

2 . Вычисление площадей многоугольников

Площадь многоугольника на клетчатой бумаге измеряется квадратными единицами: мм², см². Но в качестве единицы площади можно рассматривать и клетку.

Пусть размер клетки 1×1.

1. Легко найти площадь прямоугольника и прямоугольного треугольника.

Площадь прямоугольника: S= 4 ×10 =40(кв.ед.)

Площадь прямоугольного треугольника:S= (8 ×6) : 2 = 24(кв.ед.)

Начертив многоугольник с вершинами в узлах клеток и можно найти его площадь. Это можно сделать разными способами.

1 способ.

Разделим многоугольник на части – прямоугольники и прямоугольные треугольники с вершинами в узлах клеток, стороны которых проходят по линиям. В полученном многоугольнике легко посчитать площади частей, сложить их, чтобы найтиискомую площадь многоугольника.

1)Найдём площадь фигуры ABCD.

S = S₁ + S₂ + S₃ + S₄ =(1×4)÷2+(1×3)÷2+(1×1)+(1×2)÷2=2+1,5+1+1=5,5(кв.ед.)

2)Найдём площадь фигуры

2 способ.

Достраиваем искомую фигуру до прямоугольника.

Находим площадь всех получившихся дополнительных фигур и площадь самого прямоугольника.

Из площади прямоугольника вычитаем сумму площадей всех лишних фигур.

З начит и правда клетка помогает! И строить! И измерять! Ведь клетка это квадрат. Его сторонами можно измерять длины отрезков, а самими квадратами можно измерять площадь. Но главное волшебство клетки мы открыли в её узлах - точках, являющихся вершинами квадратов-клеток. Об этом нашем открытии пойдёт речь в следующей главе.

3.Формула Пика.

Георг Александр Пик (1859-1942)

Круг его математических интересов был чрезвычайно широк. Но он больше всего известен, однако, своей теоремой Пика, которая появилась в его восьмистраничной работе 1899 года.

Для того чтобы найти площадь любой фигуры по клеточкам, можно использовать формулу Пика.

Данная формула основана на подсчёте количества узлов, лежащих внутри фигуры и на её границе.

Узел – это точка, которая лежит на пересечении 2 линий данной сетки: вертикальных и горизонтальных.

Площадь фигуры по клеточкам находится по формуле:

В – количество узлов, которые находятся внутри фигуры.

Г – количество узлов, которые находятся на границах (на вершинах и сторонах).

Примеры нахождения площади по клеточкам

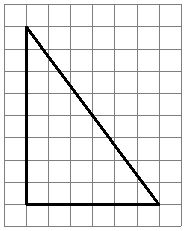
1) Найдём площадь треугольника. Отметим внутренние узлы и узлы, которые находятся на границах.

В = 7 (внутренние).

Г = 8 (узлы на границах).

Площадь треугольника S = 7 + 8/2 - 1 = 10 ( кв. ед.)

4. Построение фигур по заданной площади.

Умение находить площади фигур позволяет нам справиться с такими заданиями как построение фигур по заданным площадям:

1. Начертите два разных прямоугольных треугольника, площади которых равны: а) двум клеткам; б) 3 клеткам; 4,5 клетки.

2. Начертите квадрат, площадь которого равна: а) 10 клеткам; б) 17 клеткам; 26 клеткам

К летка помогает нам с детства. Стоит произнести в определённом порядке волшебные слова: «влево – вправо – вниз – вверх», как тут же появится изображение чего-либо.

5 . Игры и задачи на клетчатой бумаге.

Игры – это увлекательное занятие, особенно, если есть возможность проявить смекалку и стать победителем благодаря собственным навыкам. Есть игры, для которых нужна поверхность с квадратами, например шахматы, шашки, но есть и такие, где можно использовать специальные доски и бумагу в клеточку. Я рассмотрел следующие игры.

1) Крестики – нолики

Популярная игра в крестики – нолики состоит в следующем. Двое по очереди рисуют на листе клетчатой бумаги крестики и нолики. Первый игрок рисует крестики, второй – нолики. Выигрывает тот, кто первым поставит определённое количество своих знаков в ряд (по вертикали, горизонтали или диагонали).

2 ) «Морской бой»

3) Ползунок.

Эта игра была придумана Д. Силверменом, автором довольно известной книги "Ваш ход". Игровое поле представляет собой решетку размером 5×6 точек (можно играть и на полях других размеров).

Играют двое, проводя по очереди горизонтальные или вертикальные "единичные" отрезки. Требуется, чтобы получающаяся траектория игры была непрерывной, однако присоединять новый отрезок к уже имеющейся ломаной можно с любого конца. Проигрывает тот, кто вынужден своим ходом замкнуть траекторию. Например, в позиции на рис. 6 тот, чья очередь ходить, проигрывает.

Задачи на разрезание.

1. Разрежьте фигуру на 4 равные части.

Ответ:

Заключение

Значит и правда клетка помогает! И строить! И измерять! Ведь клетка это квадрат. Его сторонами можно измерять длины отрезков, а самими квадратами можно измерять площадь. Но главное волшебство клетки мы открыли в её узлах - точках, являющихся вершинами квадратов-клеток. Они, как звёзды на небе открывают нам созвездия геометрических фигур и их свойства.

Головоломки увлекают решением задач на клетчатой бумаге, заставляют проявить свою смекалку.

При выполнении проекта я расширила свои знания о решении задач на клетчатой бумаге, убедилась в их многообразии. Я научилась вычислять площади многоугольников, нарисованных на клетчатом листке, узнала, как раскраска клеточек помогает решать многие задачи, а также познакомилась поближе с задачами на разрезание и, наконец, научился играть в увлекательные игры на листке бумаги в клетку. Таким образом, обычная тетрадь по математике вовсе не обычная. Клетка позволяет ей совершать настоящие чудеса!

Литература:

1. И.Ф. Шарыгин, Л.Н. Ерганжиева «Наглядная геометрия»: учебное пособие для 5-6 классов – Смоленск: Русич,1995

2. https://math6-vpr.sdamgia.ru/test?theme=1

https://botana.cc/prepod/_bloks/pic/ym6b0om-002.jpg

https://ds04.infourok.ru/uploads/ex/126a/000123d9-ffd2fd4a/2/img8.jpg

https://ds04.infourok.ru/uploads/ex/091d/00001ca4-ef5c74ff/7/img5.jpg

http://900igr.net/up/datas/64119/004.jpg

http://ucthat-v-skole.ru/zagruzki/tangram-shema.docx

https://ot2do6.ru/uploads/posts/2016-03/1459430485_11.jpg

https://from-ua.com/upload/32ea79242aa2436.jpg