Подготовка к ОГЭ. Теория по теме "Треугольники".

A

C

Треугольником называется фигура, которая состоит из трёх точек, не лежащих на одной прямой, и трёх отрезков, попарно соединяющих эти точки.

Обозначение: ABC, BCA, CAB

Периметр – сумма длин всех сторон

P_ABC = AB + BC + AC

Элементы:

Вершины – A, B, C (точки)

Стороны – AB, BC, AC (отрезки)

Углы – BAC , ABC,  ACB (A, B, C)

Сумма углов треугольника равна 180º, т.е. A+ B+ C = 180

Внешний угол треугольника – угол, смежный с одним из углов треугольника

2

4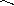

Внешний угол треугольника

1) равен сумме двух углов треугольника, не смежных с ним, 4 = 1 + 2

2) больше любого внутреннего угла, не смежного сним,

4 1, 4 2

Виды треугольников

Остроугольный

Прямоугольный

Тупоугольный

Разносторонние (все стороны разные)

все углы острые (меньше 90)

один угол прямой (равен 90)

один угол тупой (больше 90)

Равнобедренные (две стороны равны – боковые)

45

45

90

Равносторонние (все стороны равны)

60

60

60

Основные линии в треугольнике

Медиана

(отрезок, соединяющий верщину треугольника с серединой противолежащей стороны этого треугольника)

Биссектриса

(отрезок биссектрисы угла треугольника, соединяющий вершину с точкой на противолежащей стороне этого треугольника)

Высота

(перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону этого треугольника)

B

C

M

A

B

D

A

B

C

H

A

C

BH  AC

Средняя линия реугольника

B

A

C

M

N

MN - средняя линия

М – середина АВ (AM = MB)

N – середина ВС (BN = NC)

Свойство:

MN  AC

MN = AC

Соотношения между сторонами и углами треугольников

Против большей стороны лежит больший угол, и наоборот, против большего угла лежит большая сторона.

Сравните углы треугольника АВС, если АВBCAC.

Ответ. CAB

В равных треугольниках против равных сторон лежат равные углы, и наоборот, против равных углов лежат равные стороны.

Любая сторона треугольника меньше суммы двух других сторон и больше их разности a b – c;

b a – c;

c a – b .

Существует ли треугольник со сторонами 5см, 8см и 12см?

5

8

12 Ответ. не существует

Признаки равенства треугольников

Признаки подобия треугольников

• По двум сторонам и углу между ними

• По стороне и двум прилежщим к ней углам

• По трем сторонам

• По двум пропорциональным сторонам и углу между ним

• По двум равным углам

• По трем пропорциональным сторонам

боковая сторона

боковая сторона

основание

Равнобедренный треугольник — треугольник у которого равны две стороны.

Равносторонний треугольник — треугольник у которого все стороны равны.

Формулы для вычисления площади треугольника

a

h

a – сторона

h – высота

a

c

h

b

Прямоугольный треугольник

a, b – катеты

с - гипотенуза

h – высота

a, b, c – стороны

p – полупериметр

b

a



b

c

– формула Герона

a

Равносторонний треугольник

r – радиус вписанной окружности

p - полупериметр

a, b, c – стороны

R – радиус описанной окружности

a

Элементы равностороннего треугольника

Высота (h)

Радиус вписанной окружности (r)

Радиус описанной окружности (R)