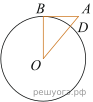Подготовка к ОГЭ по геометрии

Вариант 1

1.  Один из острых углов прямоугольного треугольника равен 34°. Найдите его другой острый угол. Ответ дайте в градусах.

2.Хорды AC и BD окружности пересекаются в точке P, BP  =  15, CP  =  6, DP  =  10. Найдите AP.

3. Найдите площадь прямоугольника, если его периметр равен 44 и одна сторона на 2 больше другой.

4.На клетчатой бумаге с размером клетки 1х1 изображена фигура. Найдите её площадь.

5. Какие из следующих утверждений верны?

1)  Сумма углов выпуклого четырехугольника равна 180°.

2)  Если один из углов параллелограмма равен 60°, то противоположный ему угол равен 120°.

3)  Диагонали квадрата делят его углы пополам.

4)  Если в четырехугольнике две противоположные стороны равны, то этот четырехугольник  — параллелограмм.

Если утверждений несколько, запишите их номера в порядке возрастания.

6.  Найдите угол АСО, если его сторона СА касается окружности, О  — центр окружности, а дуга AD окружности, заключённая внутри этого угла, равна 100°.

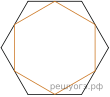
7. Дан правильный шестиугольник. Докажите, что если последовательно соединить отрезками середины его сторон, то получится правильный шестиугольник.

Вариант 2

1.Угол A трапеции ABCD с основаниями AD и BC, вписанной в окружность, равен 81°. Найдите угол C этой трапеции. Ответ дайте в градусах.

2.Отрезок AB  =  40 касается окружности радиуса 75 с центром O в точке B. Окружность пересекает отрезок AO в точке D. Найдите AD.

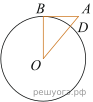
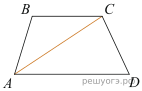
3.В трапеции ABCD известно, что AD=9, BC=6, а её площадь равна 75. Найдите площадь треугольника ABC.

4. На клетчатой бумаге с размером клетки 1см x 1см отмечены точки А, В и С. Найдите расстояние от точки А до середины отрезка ВС. Ответ выразите в сантиметрах.

5. Какие из данных утверждений верны? Запишите их номера.

1)  На плоскости существует единственная точка, равноудалённая от концов отрезка.

2)  В любой треугольник можно вписать окружность.

3)  Если в параллелограмме две смежные стороны равны, то такой параллелограмм является ромбом.

6. Прямая, параллельная основаниям MP и NK трапеции MNKP, проходит через точку пересечения диагоналей трапеции и пересекает её боковые стороны MN и KP в точках 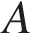  и 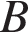  соответственно. Найдите длину отрезка AB, если  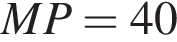 см,   см.

7. В окружности через середину O хорды AC проведена хорда BD так, что дуги AB и CD равны. Докажите, что O  — середина хорды BD.