Билет №1
П араллелограмм (определение, свойства, доказательство одного из свойств).
араллелограмм (определение, свойства, доказательство одного из свойств).
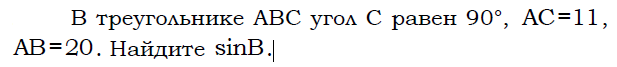
2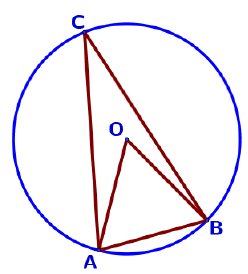
 .
.
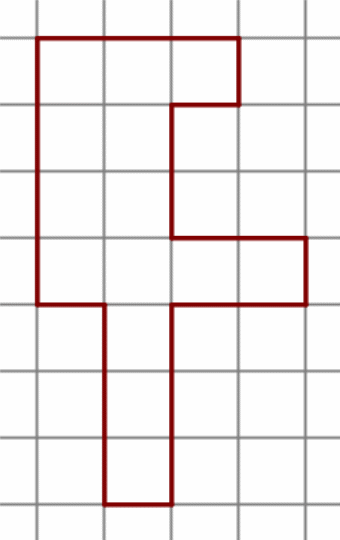
На клетчатой бумаге с размером клетки 1 см × 1 см изображена фигура. Найдите её площадь.
Найдите сумму внутренних углов выпуклого: а) четырехугольника, б) шестиугольника, в) одиннадцатиугольника
Найдите острый угол параллелограмма ABCD, если биссектриса угла A образует со стороной BC угол, равный 15°. Ответ дайте в градусах.
Вставьте пропущенное слово:
а) Отрезок, соединяющий центр окружности с какой-либо точкой окружности, называется ____________________ окружности.
б) Хорда, проходящая через центр окружности, называется ___________.
в) Отрезок, соединяющий две точки окружности, называется __________.
г) Центр окружности является _________________ любого диаметра.
8. а) Из точки В проведены две касательные к окружности с центром в точке О. Найдите расстояние от точки В до точки касания с окружностью, если угол между касательными равен 120°, а расстояние от точки В до точки О равно 26.
б) Из точки В проведены две касательные к окружности с центром в точке О. Найдите расстояние от точки В до точки касания с окружностью, если угол между касательными равен 90°, а радиус окружности равен 17.
в) Из точки В проведены две касательные к окружности с центром в точке О. Найдите расстояние от точки В до точки касания с окружностью, если угол между касательными равен 120°, а расстояние от точки В до точки О равно 38.
Билет №2
П араллелограмм (определение, признаки, доказательство одного из признаков).
араллелограмм (определение, признаки, доказательство одного из признаков).
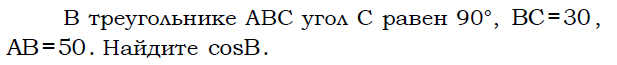

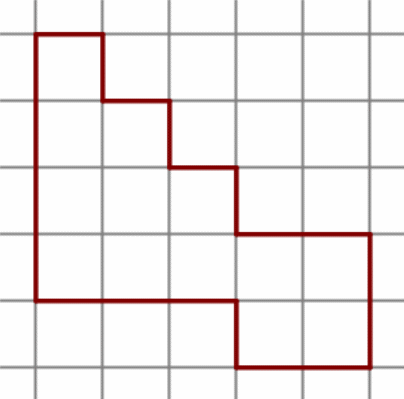
На клетчатой бумаге с размером клетки 1 см × 1 см изображена фигура. Найдите её площадь.
а) Один из углов параллелограмма равен 74°. Найдите больший угол этого параллелограмма. Ответ дайте в градусах б) Один из углов параллелограмма равен 26°. Найдите больший угол этого параллелограмма. Ответ дайте в градусах. в) Один из углов параллелограмма равен 96°. Найдите меньший угол этого параллелограмма. Ответ дайте в градусах
а) Один из углов параллелограмма на 300больше другого. Найдите острый угол параллелограмма. Ответ дайте в градусах
Выберите верное утверждение Касательной к окружности называется:
а) Прямая, которая пересекает окружность. б) Прямая, имеющая с окружностью только одну общую точку. в) Прямая, имеющая с окружностью общие точки.
г) Отрезок, имеющий с окружностью только одну общую точку
8. а) Из точки А проведены две касательные к окружности с центром в точке О. Найдите радиус окружности, если угол между касательными равен 60°, а расстояние от точки А до точки О равно 6.
б) Из точки А проведены две касательные к окружности с центром в точке О. Найдите расстояние от точки А до точки О, если угол между касательными равен 60°, а радиус окружности равен 8.
в) Из точки А проведены две касательные к окружности с центром в точке О. Найдите расстояние от точки А до точки О, если угол между касательными равен 60°, а радиус окружности равен 6
Билет №3
П рямоугольник (определение, свойство прямоугольника с доказательством).
рямоугольник (определение, свойство прямоугольника с доказательством).

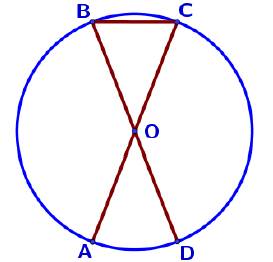
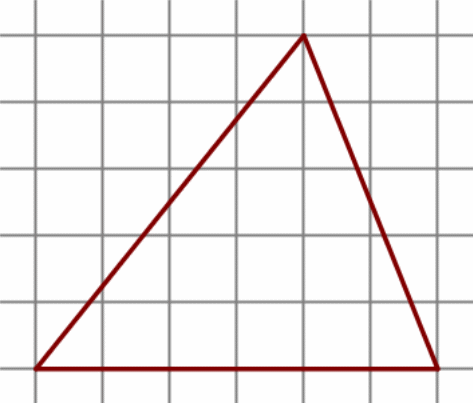
На клетчатой бумаге с размером клетки 1 см × 1 см изображена фигура. Найдите её площадь.
Закончите предложение. Расстоянием от точки до прямой называется: а) длина перпендикуляра, проведенного от данной точки к прямой, б) расстояние между данной точкой и любой точкой прямой, в) часть прямой, ограниченная двумя точками, г) прямая, проходящая через данную точку и произвольную точку на прямой.
А) В ромбе ABCD угол ABC равен 72°. Найдите угол ACD. Ответ дайте в градусах.
б) В ромбе ABCD угол ABC равен 84°. Найдите угол ACD. Ответ дайте в градусах. в) В ромбе ABCD угол ABC равен 56°. Найдите угол ACD. Ответ дайте в градусах.
7. а) Диагонали ромба равны 18 и 24. Найдите периметр ромба.
б) Диагонали ромба равны 40 и 30. Найдите периметр ромба.
в) Диагонали ромба равны 48 и 14. Найдите периметр ромба.
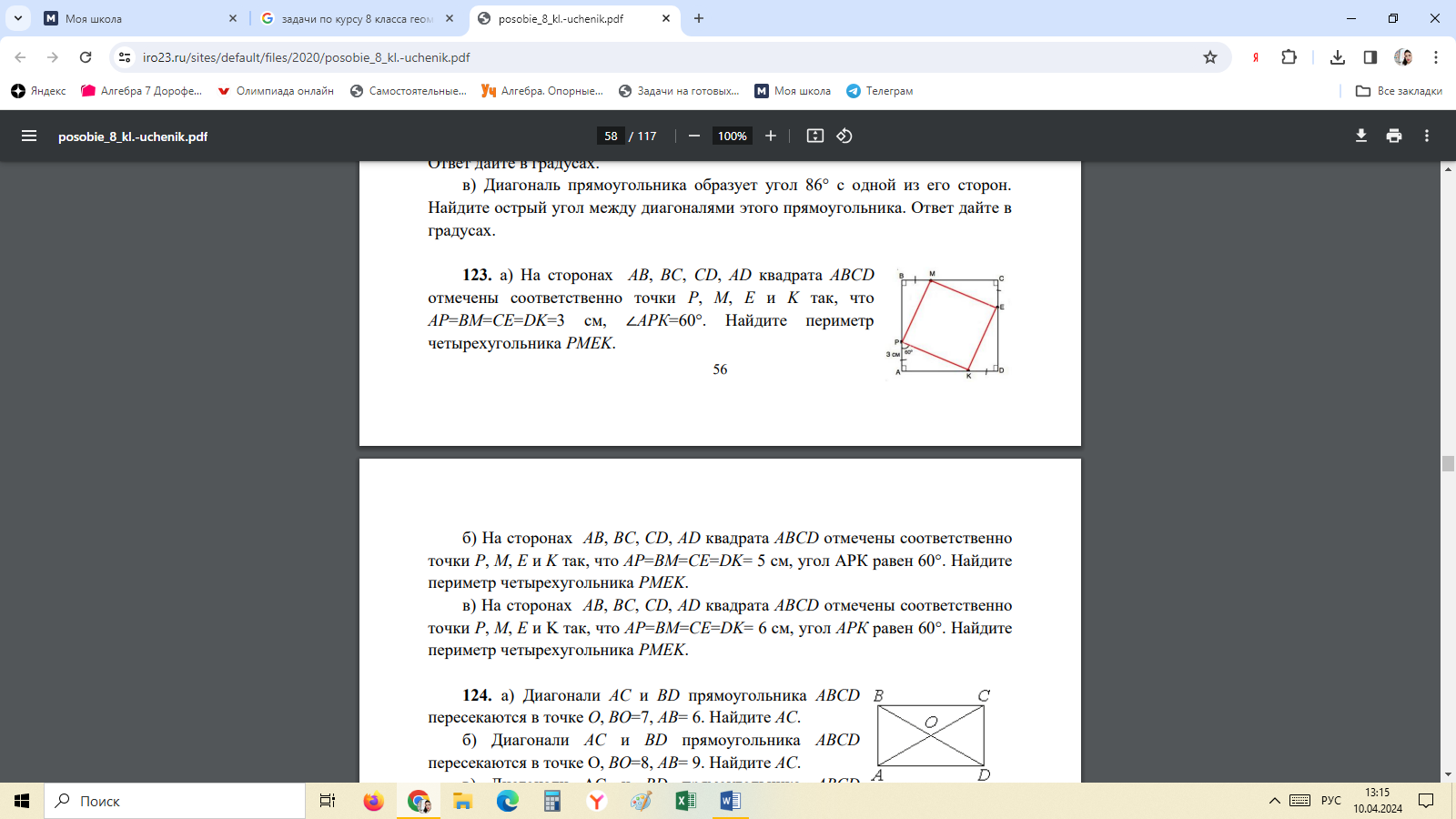
8. На сторонах AB, BC, CD, AD квадрата ABCD отмечены соответственно точки P, M, E и K так, что AP=BM=CE=DK=3 см, ∠АРК=60°. Найдите периметр четырехугольника PMEK.
Билет №4
Р омб и квадрат (определения, свойства, доказательство свойства диагоналей ромба).
омб и квадрат (определения, свойства, доказательство свойства диагоналей ромба).


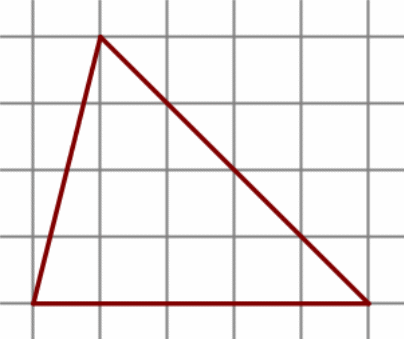
На клетчатой бумаге с размером клетки 1 см × 1 см изображена фигура. Найдите её площадь.
Около окружности описана равнобокая трапеция с основаниями 5 и 3. Найдите радиус окружности.
В равнобедренный треугольник АВС вписана окружность. Параллельно его основанию АС проведена касательная к окружности, пересекающая боковые стороны в точках D и Е. Найдите радиус окружности, если DЕ = 8, АС = 18.
В четырёхугольнике ABCD углы B и D — прямые. Диагональ AC образует со стороной AB острый угол в 40°, а со стороной AD - угол в 30°. Найдите острый угол между диагоналями AC и BD.
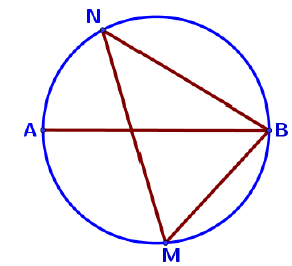
Найдите углы вписанного в окружность четырехугольника, если три угла (в последовательном порядке) относятся как 4:7:6. В ответе укажите больший из них в градусах.
Детская песочница во дворе имеет форму круга диаметром 4 м. Какова ее площадь? (Число π округлите до сотых)
Длина окружности обода колеса равна 6,3 м. Вычислите диаметр колеса. (π округлите до целых).
Колесо на расстоянии 390 м сделало 150 оборотов. Найдите диаметр колеса. (π=3,14). Результат запишите в метрах, округлив до сотых.
Сторона квадрата равна 16 см. Найдите площадь закрашенной части круга .Число П округлите до целых. 
Билет №5
Теорема о площади прямоугольника. Площадь квадрата.



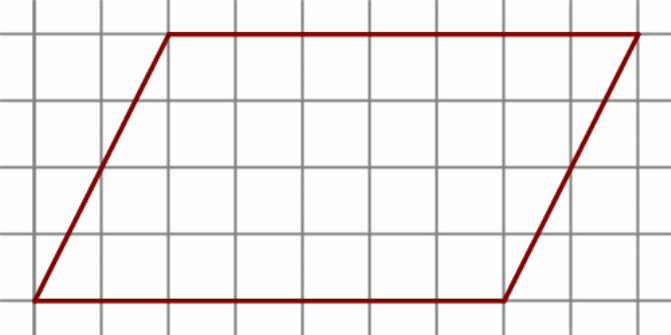
На клетчатой бумаге с размером клетки 1 см × 1 см изображена фигура. Найдите её площадь.
----------------------------------------------------------------------------------------------------
Билет №6
Теорема о площади параллелограмма.



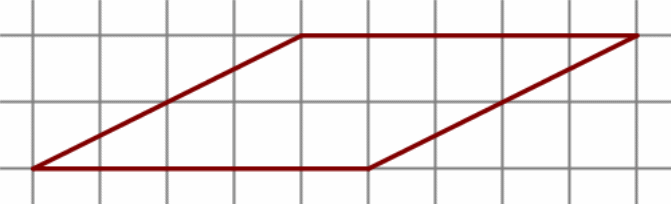
На клетчатой бумаге с размером клетки 1 см × 1 см изображена фигура. Найдите её площадь.
Билет №7
 Теорема о площади треугольника.
Теорема о площади треугольника.
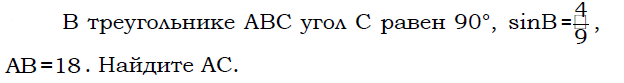

Н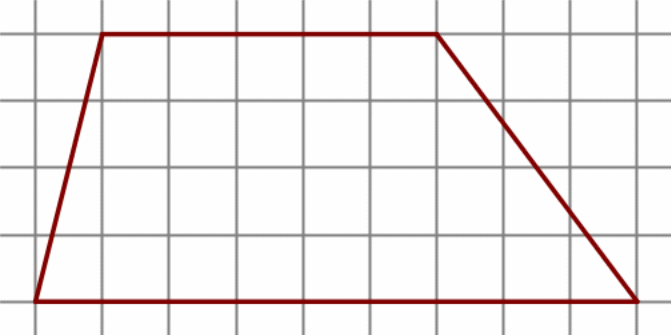 а клетчатой бумаге с размером клетки 1 см × 1 см изображена фигура. Найдите её площадь.
а клетчатой бумаге с размером клетки 1 см × 1 см изображена фигура. Найдите её площадь.
----------------------------------------------------------------------------------------------------
Билет №8
Т еорема о площади трапеции.
еорема о площади трапеции.
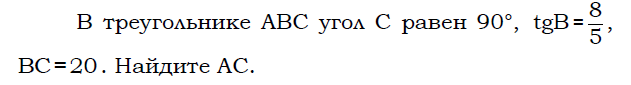

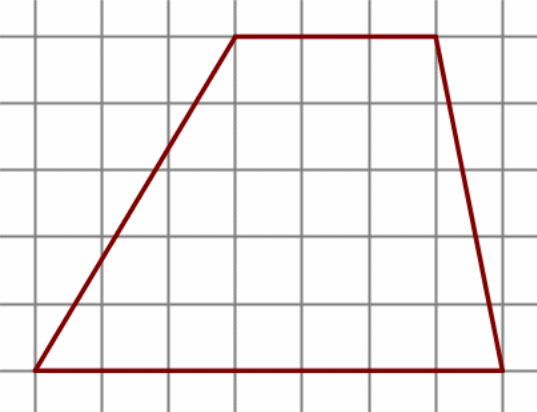
На клетчатой бумаге с размером клетки 1 см × 1 см изображена фигура. Найдите её площадь.
Билет №9
Т еорема Пифагора.
еорема Пифагора.
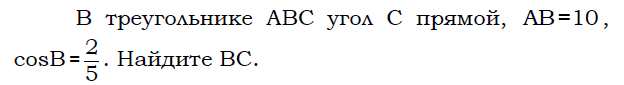
3
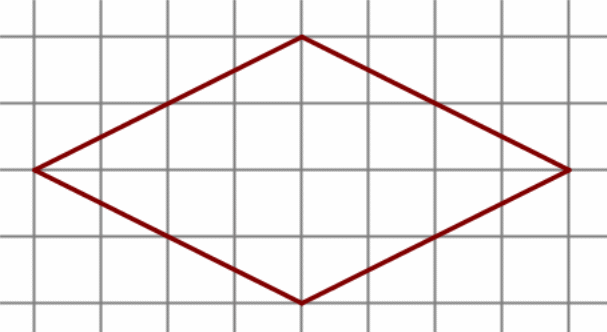 .
.
4.На клетчатой бумаге с размером клетки 1 см × 1 см изображена фигура. Найдите её площадь.
----------------------------------------------------------------------------------------------------
Билет №10
Определение подобных треугольников. Теорема об отношении площадей
п одобных треугольников.
одобных треугольников.

3
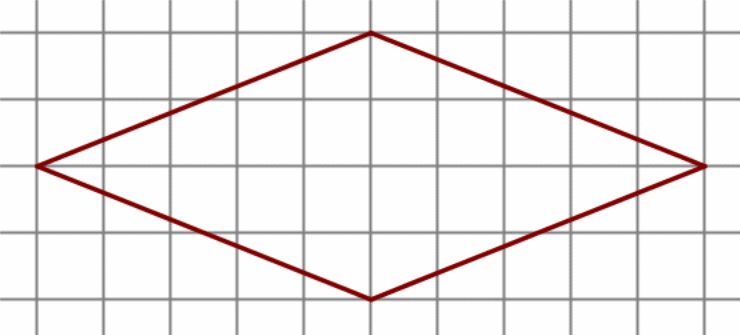 .
.
4. На клетчатой бумаге с размером клетки 1 см × 1 см изображена фигура. Найдите её площадь.
Билет №11
Признаки подобия треугольников (доказательство одного из признаков).



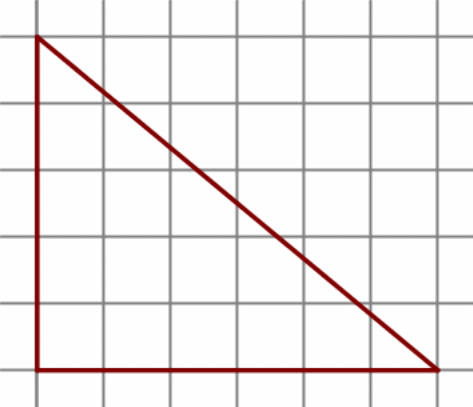
На клетчатой бумаге с размером клетки 1 см × 1 см изображена фигура. Найдите её площадь.
----------------------------------------------------------------------------------------------------
Билет №12

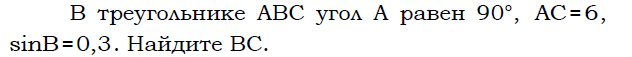 Средняя линия треугольника (определение, теорема).
Средняя линия треугольника (определение, теорема).

3.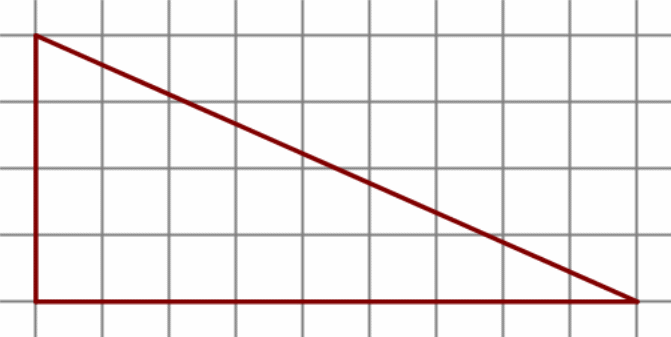
4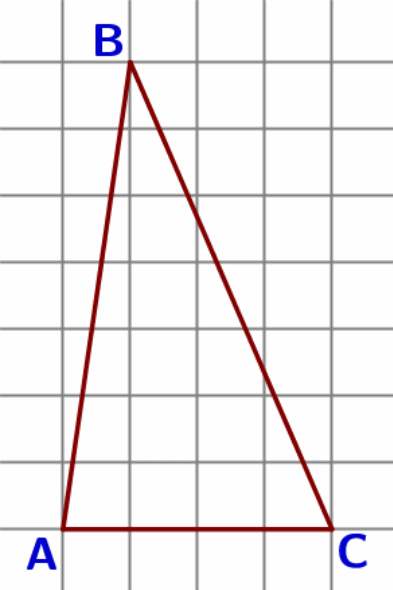 . На клетчатой бумаге с размером клетки 1 см × 1 см изображена фигура. Найдите её площадь.
. На клетчатой бумаге с размером клетки 1 см × 1 см изображена фигура. Найдите её площадь.
Билет №13
Синус, косинус и тангенс острого угла прямоугольного треугольника (определения, основные формулы, таблица значений синуса, косинуса и тангенса углов 300, 450 , 600 ).

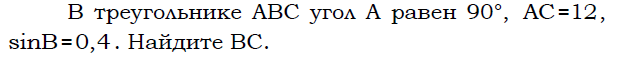

3 .
.
4. На клетчатой бумаге с размером клетки 1 см × 1 см изображена фигура. Найдите её площадь.
----------------------------------------------------------------------------------------------------
Билет №14
Взаимное расположение прямой и окружности (рассмотреть 3 случая, сделать чертежи).

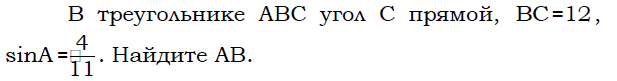

3.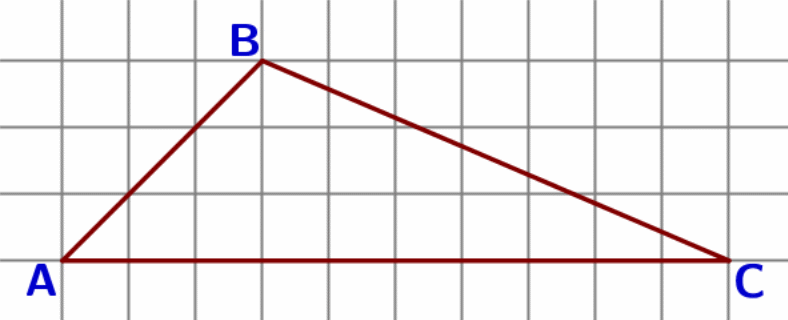
4. На клетчатой бумаге с размером клетки 1 см × 1 см изображена фигура. Найдите её площадь.
Билет №15
К
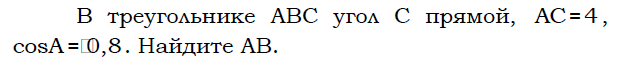 асательная к окружности (определение, теорема).
асательная к окружности (определение, теорема).

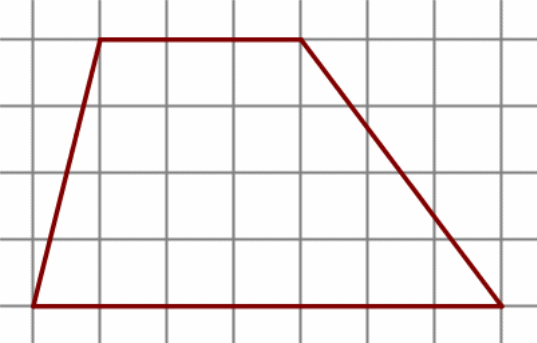
3.
4. На клетчатой бумаге с размером клетки 1 см × 1 см изображена фигура. Найдите её площадь.
----------------------------------------------------------------------------------------------------
Билет №16
В
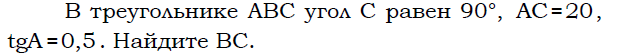 писанный угол (определение, теорема о вписанном угле).
писанный угол (определение, теорема о вписанном угле).

4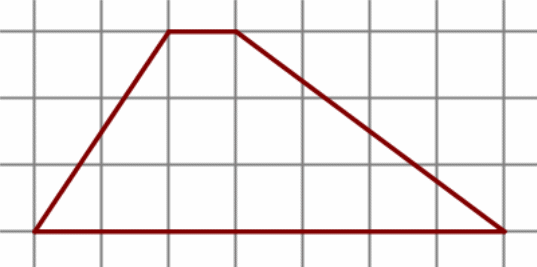 . На клетчатой бумаге с размером клетки 1 см × 1 см изображена фигура. Найдите её площадь.
. На клетчатой бумаге с размером клетки 1 см × 1 см изображена фигура. Найдите её площадь.
 Билет №17
Билет №17
Свойства биссектрисы угла (теорема).
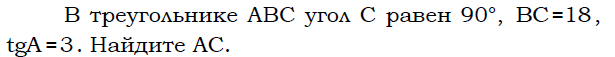


На клетчатой бумаге с размером клетки 1 см × 1 см изображена фигура. Найдите её площадь.
----------------------------------------------------------------------------------------------------
Билет №18
Свойства серединного перпендикуляра к отрезку (определение, теорема).



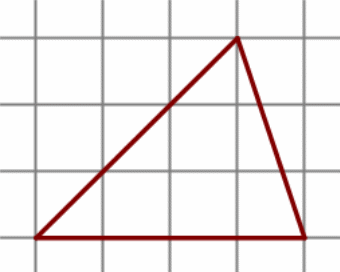
На клетчатой бумаге с размером клетки 1 см × 1 см изображена фигура. Найдите её площадь.
Билет №19
Вписанная окружность (определение, теорема, свойства).
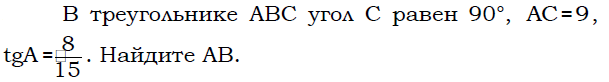


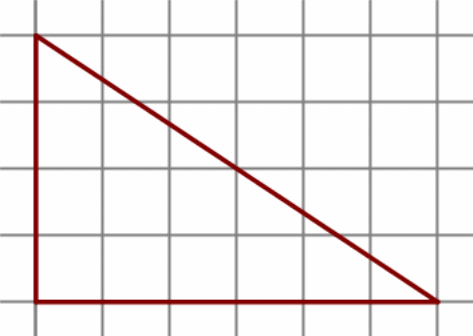
4. На клетчатой бумаге с размером клетки 1 см × 1 см изображена фигура. Найдите её площадь.
-----------------------------------------------------------------------------------------------
Билет №20
Описанная окружность (определение, теорема, свойства).

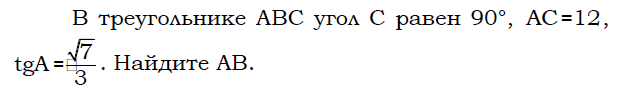


Н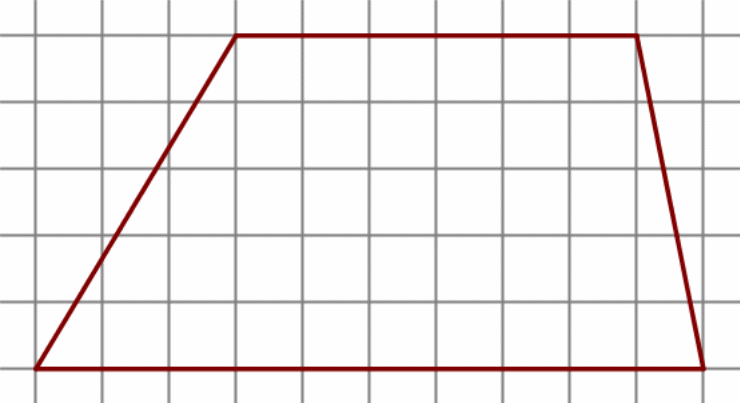 а клетчатой бумаге с размером клетки 1 см × 1 см изображена фигура. Найдите её площадь.
а клетчатой бумаге с размером клетки 1 см × 1 см изображена фигура. Найдите её площадь.






 араллелограмм (определение, свойства, доказательство одного из свойств).
араллелограмм (определение, свойства, доказательство одного из свойств).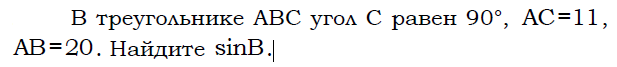

 .
.


















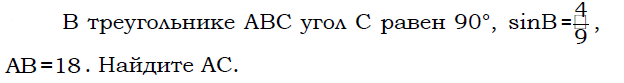

 а клетчатой бумаге с размером клетки 1 см × 1 см изображена фигура. Найдите её площадь.
а клетчатой бумаге с размером клетки 1 см × 1 см изображена фигура. Найдите её площадь. 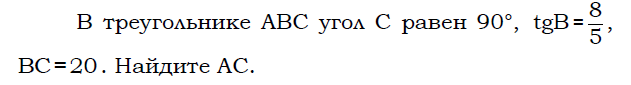


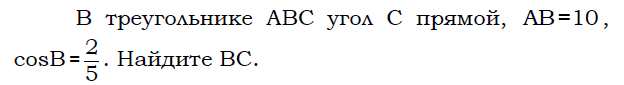

 .
.

 .
.




 . На клетчатой бумаге с размером клетки 1 см × 1 см изображена фигура. Найдите её площадь.
. На клетчатой бумаге с размером клетки 1 см × 1 см изображена фигура. Найдите её площадь.
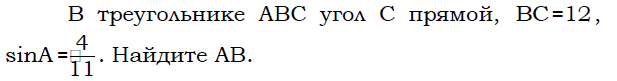





 . На клетчатой бумаге с размером клетки 1 см × 1 см изображена фигура. Найдите её площадь.
. На клетчатой бумаге с размером клетки 1 см × 1 см изображена фигура. Найдите её площадь. 






 а клетчатой бумаге с размером клетки 1 см × 1 см изображена фигура. Найдите её площадь.
а клетчатой бумаге с размером клетки 1 см × 1 см изображена фигура. Найдите её площадь. 









