Подготовка к ОГЭ Треугольники

Подготовила: учитель математики

МБОУ «Школа №54» г.Курск

Горбунова Л.А.

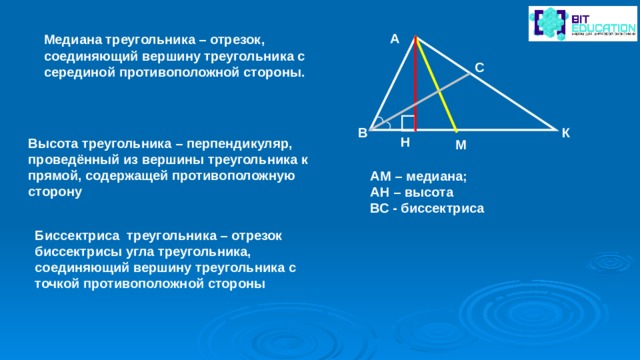
А

Медиана треугольника – отрезок, соединяющий вершину треугольника с серединой противоположной стороны.

С

В

К

Н

Высота треугольника – перпендикуляр, проведённый из вершины треугольника к прямой, содержащей противоположную сторону

М

АМ – медиана;

АН – высота

ВС - биссектриса

Биссектриса треугольника – отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны

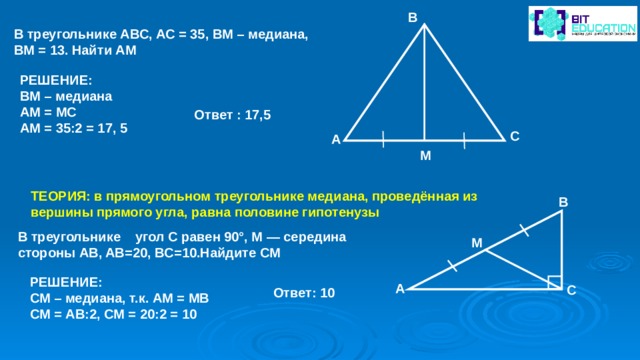
В

В треугольнике АВС, АС = 35, ВМ – медиана, ВМ = 13. Найти АМ

РЕШЕНИЕ:

ВМ – медиана

АМ = МС

АМ = 35:2 = 17, 5

Ответ : 17,5

С

А

М

ТЕОРИЯ: в прямоугольном треугольнике медиана, проведённая из вершины прямого угла, равна половине гипотенузы

B

В треугольнике    угол C равен 90°, M — середина стороны AB, AB=20, BC=10.Найдите CM

M

РЕШЕНИЕ:

СМ – медиана, т.к. АМ = МВ

СМ = АВ:2, СМ = 20:2 = 10

A

C

Ответ: 10

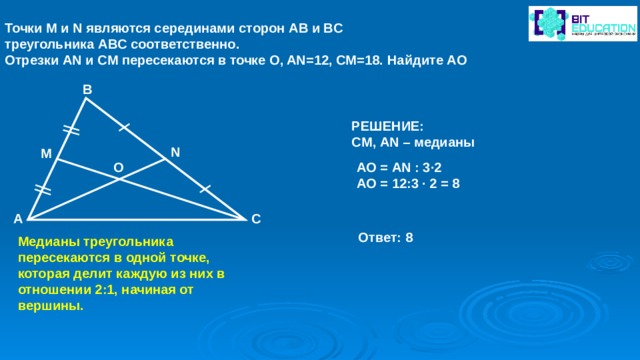
Точки M и N являются серединами сторон AB и BC 

треугольника ABC соответственно.

Отрезки AN и CM пересекаются в точке O, AN=12, CM=18. Найдите AO

B

РЕШЕНИЕ:

CM , AN – медианы

N

M

O

АО = AN : 3∙2

АО = 12:3 ∙ 2 = 8

C

A

Ответ: 8

Медианы треугольника пересекаются в одной точке, которая делит каждую из них в отношении 2:1, начиная от вершины. 

В равностороннем треугольнике любая медиана является высотой и биссектрисой .

В равнобедренном треугольнике медиана, опущенная на основание, является биссектрисой и высотой.

Теорема Пифагора:

В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов

В

Задача

Сторона равностороннего треугольника равна 12√3.

Найдите его высоту

РЕШЕНИЕ:

ВН – высота, следовательно по свойству является медианой

АН = АС : 2

А

С

Н

Из треугольника АВН по теореме Пифагора ВН 2 = АВ 2 – АН 2

ВН 2 = (12√3) 2 – (6√3) 2 = 432 – 108 = 324

ВН = 18

Ответ: 18

ПРИЗНАКИ ПОДОБИЯ ТРЕУГОЛЬНИКОВ

I. Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.

II. Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, образованные этими сторонами, равны, то такие треугольники подобны.

III. Если три стороны одного треугольника пропорциональны трём сторонам другого, то такие треугольники подобны.

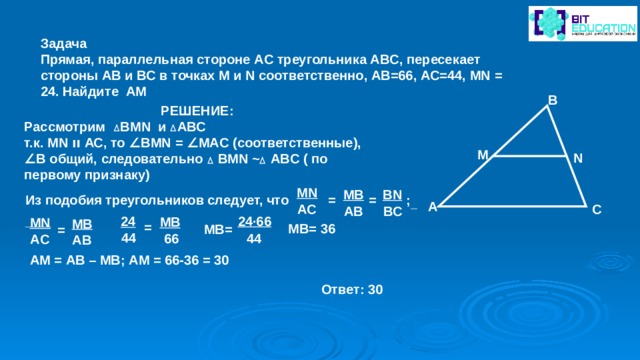
Задача

Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно, AВ=66, АС=44, MN = 24. Найдите  АM

В

РЕШЕНИЕ:

Рассмотрим ВМ N и АВС

т.к. MN װ АС, то ∠ BMN = ∠ MAC (соответственные),

∠ В общий, следовательно BMN ~ ABC ( по первому признаку)

М

N

MN

BN

MB

Из подобия треугольников следует, что = = ;

А

AC

С

AB

BC

24∙66

24

M В

MN

M В

=

МВ= 36

МВ=

=

44

66

44

AC

A В

АМ = АВ – МВ; АМ = 66-36 = 30

Ответ: 30

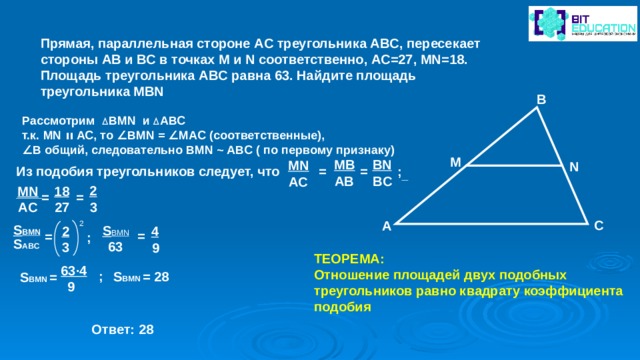
Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно, AC=27, MN=18. Площадь треугольника ABC равна 63. Найдите площадь треугольника MBN

В

Рассмотрим ВМ N и АВС

т.к. MN װ АС, то ∠ BMN = ∠ MAC (соответственные),

∠ В общий, следовательно BMN ~ ABC ( по первому признаку)

М

MB

BN

MN

N

Из подобия треугольников следует, что = = ;

AB

BC

AC

2

MN

18

=

=

3

AC

27

С

А

2

S BMN

S BMN

2

4

=

=

;

S ABC

63

3

9

ТЕОРЕМА:

Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия

63∙4

;

S BMN = 28

S BMN =

9

Ответ: 28

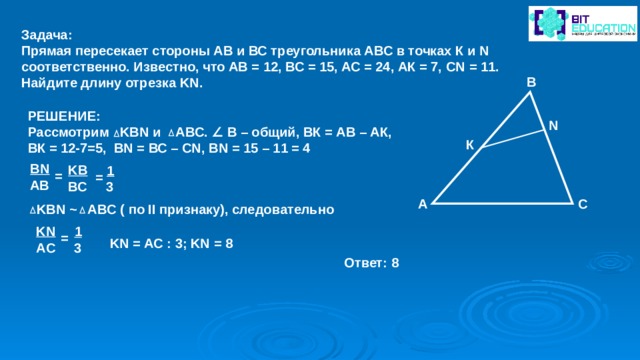
Задача:

Прямая пересекает стороны АВ и ВС треугольника АВС в точках К и N соответственно. Известно, что АВ = 12, ВС = 15, АС = 24, АК = 7, CN = 11.

Найдите длину отрезка KN .

В

РЕШЕНИЕ:

Рассмотрим KBN и АВС. ∠ В – общий, ВК = АВ – АК,

ВК = 12-7=5, BN = ВС – CN , BN = 15 – 11 = 4

N

К

BN

KB

1

=

=

AB

BC

3

А

С

KBN ~ ABC ( по II признаку), следовательно

KN

1

=

KN = АС : 3; KN = 8

AC

3

Ответ: 8

ПРОПОРЦИОНАЛЬНЫЕ ОТРЕЗКИ В ПРЯМОУГОЛЬНОМ ТРЕУГОЛЬНИКЕ

1. Высота прямоугольного треугольника, проведённая из вершины прямого угла, есть среднее пропорциональное для отрезков, на которые делиться гипотенуза этой высотой

А

CD = AD∙DB

D

AC = AD∙AB

CB = BD∙AB

В

С

2. Катет прямоугольного треугольника есть среднее пропорциональное для гипотенузы и отрезка гипотенузы, заключённого между катетом и высотой, проведённой из вершины прямого угла

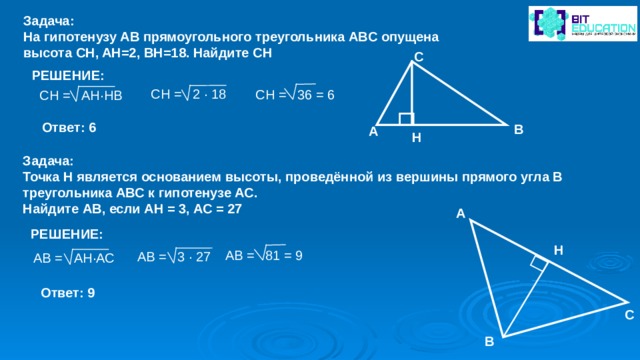
Задача:

На гипотенузу AB прямоугольного треугольника ABC опущена высота CH, AH=2, BH=18. Найдите CH

С

РЕШЕНИЕ:

C Н = 2 ∙ 18

C Н = 36 = 6

C Н = АН ∙ Н B

Ответ: 6

В

А

Н

Задача:

Точка Н является основанием высоты, проведённой из вершины прямого угла В треугольника АВС к гипотенузе АС.

Найдите АВ, если АН = 3, АС = 27

А

РЕШЕНИЕ:

Н

АВ = 81 = 9

АВ = 3 ∙ 27

АВ = АН ∙ АС

Ответ: 9

С

В

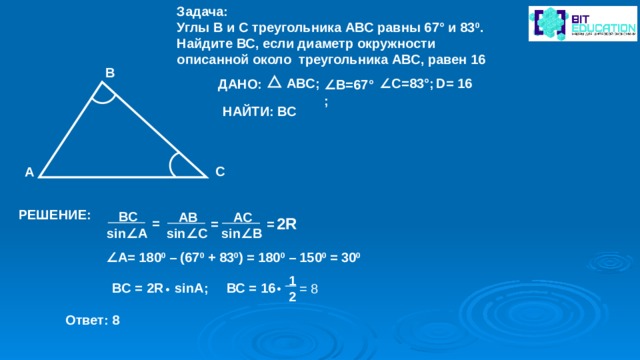
Задача:

Углы В и С треугольника АВС равны 67° и 83 0 .

Найдите ВС, если диаметр окружности описанной около треугольника АВС, равен 16

B

D= 16

АВС;

∠ C=83°;

ДАНО:

∠ B=67°;

НАЙТИ: ВС

C

A

РЕШЕНИЕ:

ВС

A С

AB

2R

=

=

=

sin ∠A

sin ∠ C

sin ∠ B

∠ A = 180 0 – (67 0 + 83 0 ) = 180 0 – 150 0 = 30 0

1

2

BC = 2R sinA ; ВС = 16

= 8

•

•

Ответ: 8

Задача:

Точка Н является основанием высоты ВН, проведённой из вершины прямого угла В прямоугольного треугольника АВС. Окружность с диаметром ВН пересекает стороны АВ и СВ в точках Р и К соответственно. Найдите РК, если ВН=14

С

РЕШЕНИЕ:

∠ ВРН = ∠ ВКН = 90 0 (вписанные углы, опирающиеся на диаметр)

∠ В = 90 0 по условию.

К

Н

•

Четырехугольник ВРНК вписан в окружность, значит

∠ Н = 90 0

Следовательно ВРНК – прямоугольник , по свойству

диагонали прямоугольника равны т.е. ВН = РК = 14

•

О

•

А

В

Р

Ответ: 14