Подготовка к ОГЭ "Треугольники"

Конкурс презентаций «Подготовка к ОГЭ и ЕГЭ»

Тема: «Треугольники»

Мальцева Надежда Валентиновна

Муниципальное бюджетное общеобразовательное учреждение «Обоянская средняя школа № 2»

Учитель математики высшей категории

2019 г

Подготовка к ОГЭ «Треугольники»

Учитель: Мальцева Надежда Валентиновна

МБОУ «Обоянская СОШ №2»

2019

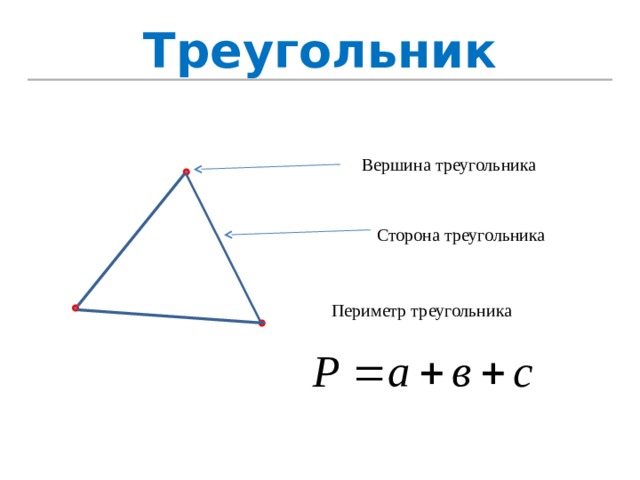
Треугольник

Вершина треугольника

Сторона треугольника

Периметр треугольника

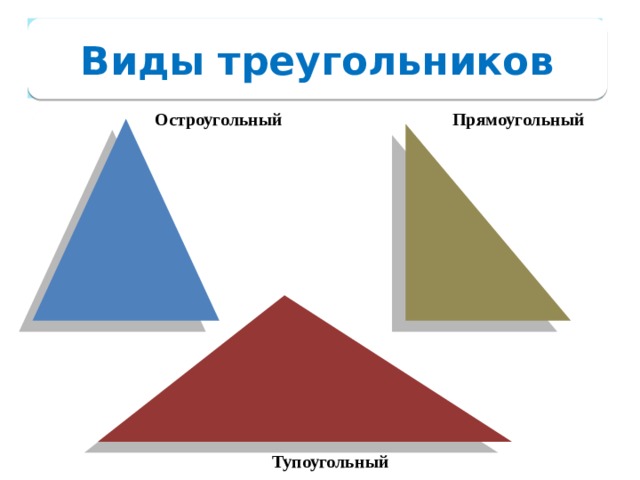
Виды треугольников

Прямоугольный

Остроугольный

Тупоугольный

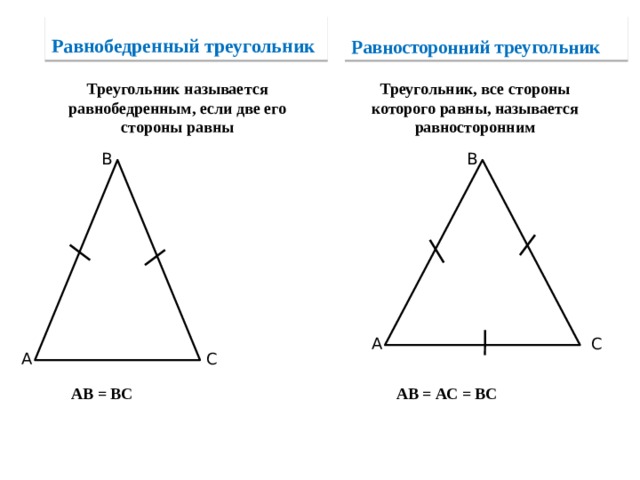
Равнобедренный треугольник

Равносторонний треугольник

Треугольник называется равнобедренным, если две его стороны равны

Треугольник, все стороны которого равны, называется равносторонним

В

В

С

А

А

С

АВ = ВС

АВ = АС = ВС

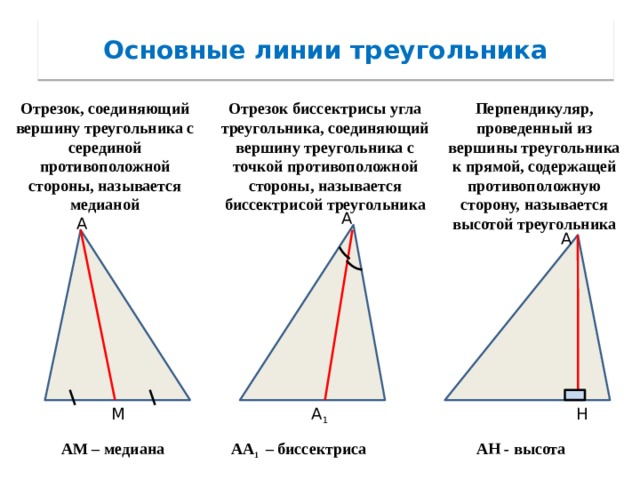
Основные линии треугольника

Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется медианой

Перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону, называется высотой треугольника

Отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны, называется биссектрисой треугольника

А

А

А

Н

А 1

М

АА 1 – биссектриса

АМ – медиана

АН - высота

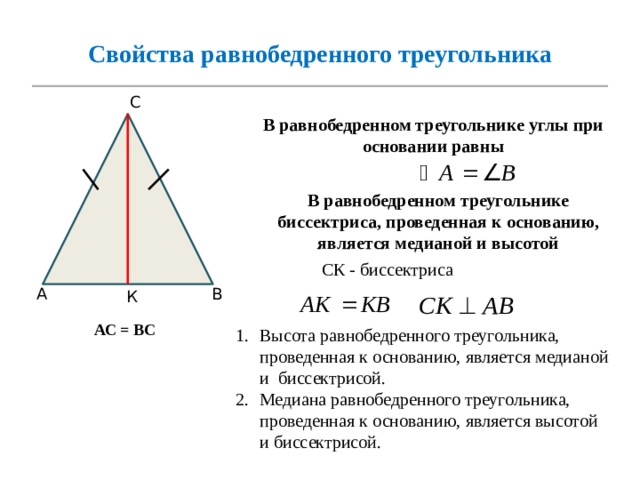
Свойства равнобедренного треугольника

С

В равнобедренном треугольнике углы при основании равны

В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой

СК - биссектриса

А

В

К

АС = ВС

• Высота равнобедренного треугольника, проведенная к основанию, является медианой и биссектрисой.
• Медиана равнобедренного треугольника, проведенная к основанию, является высотой и биссектрисой.

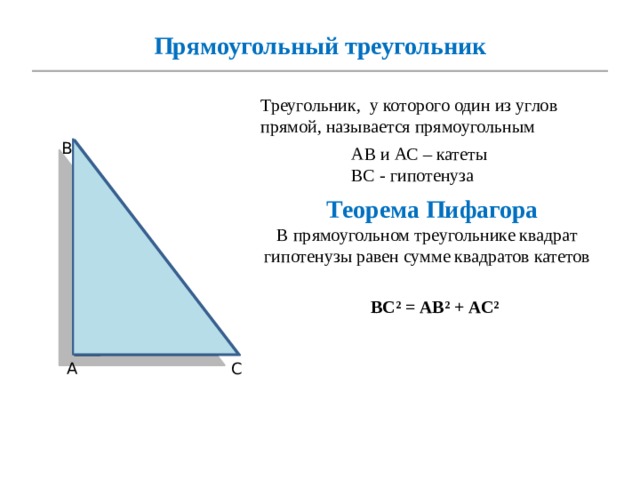
Прямоугольный треугольник

Треугольник, у которого один из углов прямой, называется прямоугольным

В

АВ и АС – катеты

ВС - гипотенуза

Теорема Пифагора

В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов

ВС² = АВ² + АС²

С

А

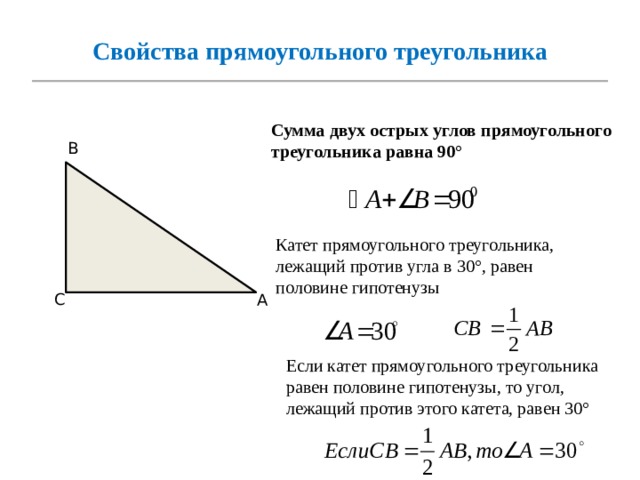
Свойства прямоугольного треугольника

Сумма двух острых углов прямоугольного треугольника равна 90°

В

Катет прямоугольного треугольника, лежащий против угла в 30°, равен половине гипотенузы

С

А

Если катет прямоугольного треугольника равен половине гипотенузы, то угол, лежащий против этого катета, равен 30°

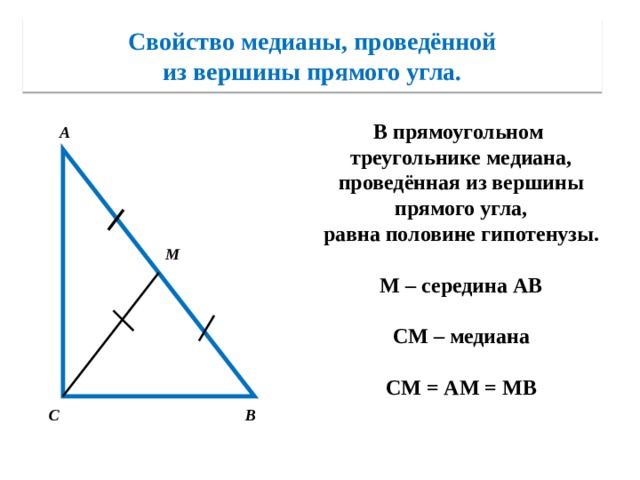
Свойство медианы, проведённой из вершины прямого угла.

В прямоугольном треугольнике медиана,

проведённая из вершины прямого угла,

равна половине гипотенузы.

М – середина АВ

СМ – медиана

СМ = АМ = МВ

А

M

С

В

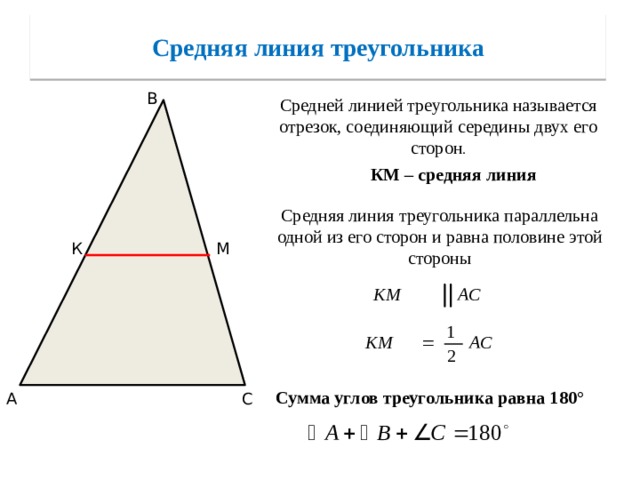
Средняя линия треугольника

В

Средней линией треугольника называется отрезок, соединяющий середины двух его сторон .

КМ – средняя линия

Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны

К

М

Сумма углов треугольника равна 180°

С

А

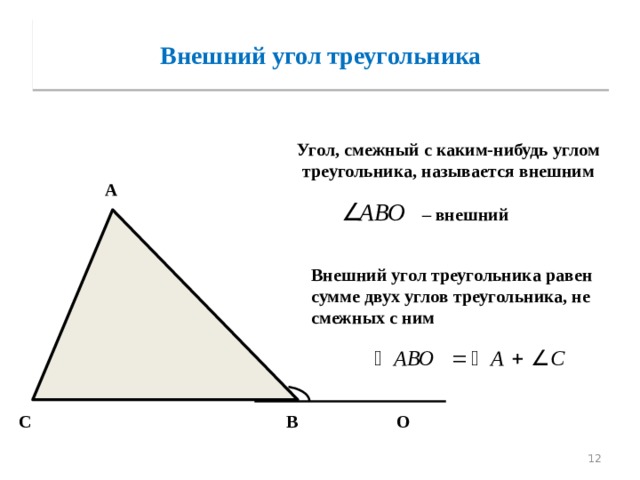
Внешний угол треугольника

Угол, смежный с каким-нибудь углом треугольника, называется внешним

A

– внешний

Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним

О

B

C

№ 1 . В равнобедренном треугольнике АВС с основанием АС внешний угол при вершине С равен 123°. Найдите величину угла АВС. Ответ дайте в градусах.

В

Решение

123°

С

А

Ответ: 66

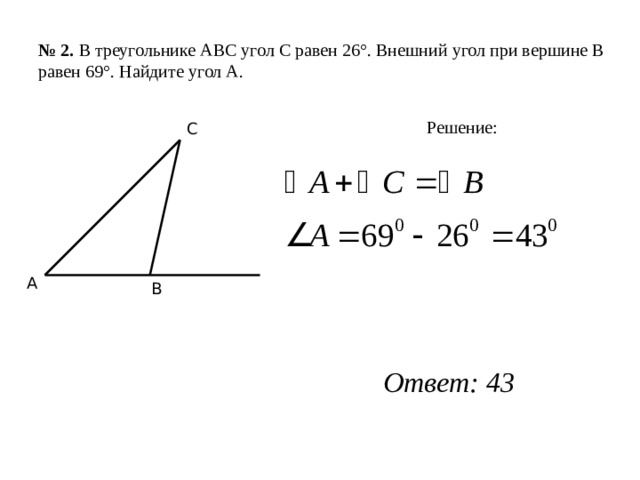
№ 2. В треугольнике АВС угол С равен 26°. Внешний угол при вершине В равен 69°. Найдите угол А.

Решение:

С

А

В

Ответ: 43

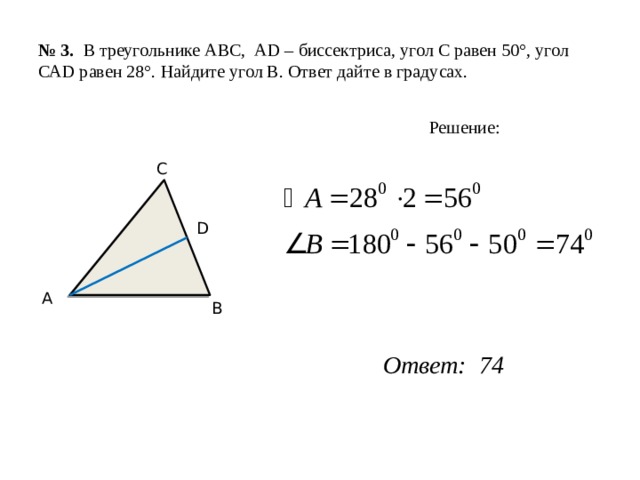
№ 3. В треугольнике АВС, АD – биссектриса, угол С равен 50°, угол САD равен 28°. Найдите угол В. Ответ дайте в градусах.

Решение:

С

D

А

В

Ответ: 74

№ 4. Один острый угол прямоугольного треугольника в два раза больше другого. Найдите меньший острый угол. Ответ дайте в градусах.

Решение:

В

С

А

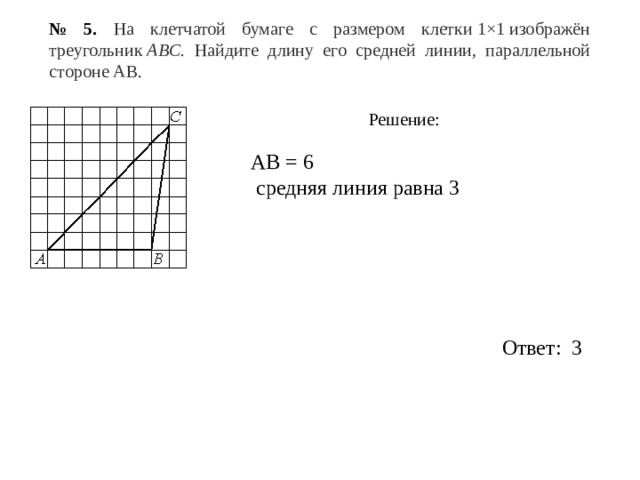
№ 5. На клетчатой бумаге с размером клетки 1×1 изображён треугольник  ABC. Найдите длину его средней линии, параллельной стороне AB.

Решение:

АВ = 6

средняя линия равна 3

Ответ: 3

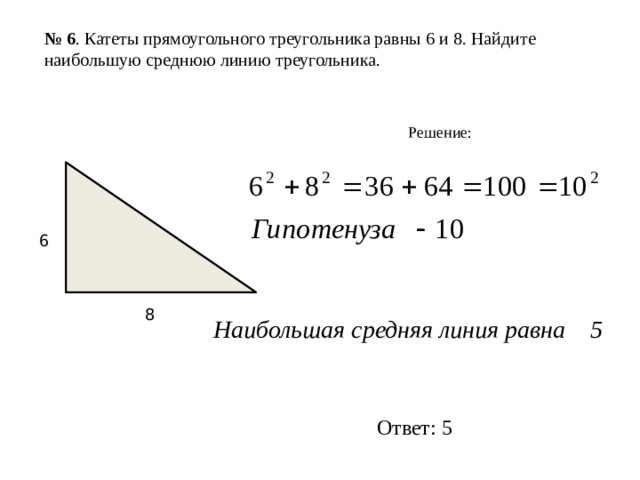
№ 6 . Катеты прямоугольного треугольника равны 6 и 8. Найдите наибольшую среднюю линию треугольника.

Решение:

6

8

Наибольшая средняя линия равна 5

Ответ: 5

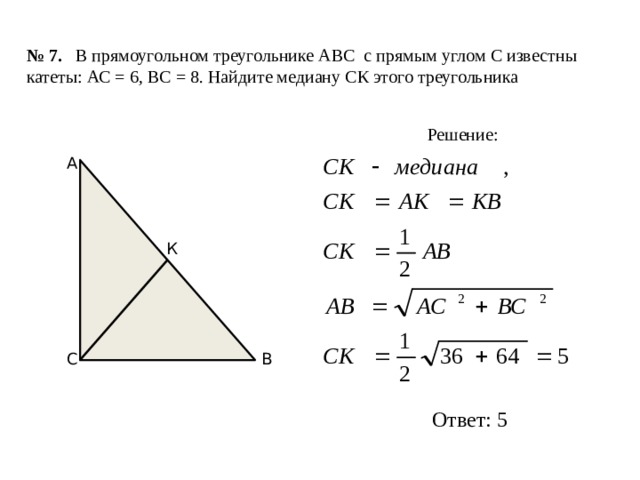
№ 7. В прямоугольном треугольнике АВС с прямым углом С известны катеты: АС = 6, ВС = 8. Найдите медиану СК этого треугольника

Решение:

А

К

С

В

Ответ: 5

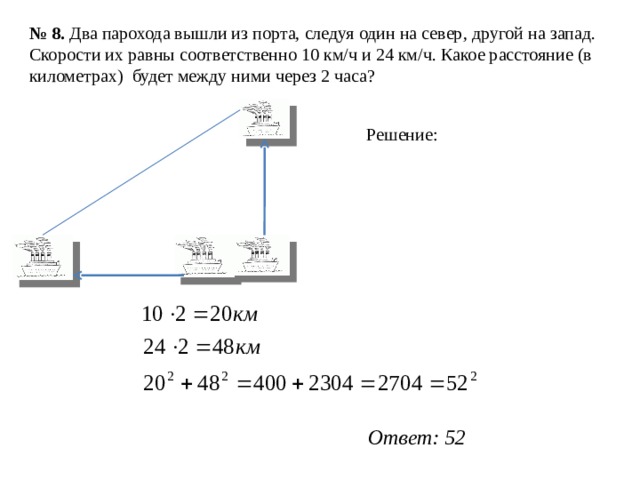
№ 8. Два парохода вышли из порта, следуя один на север, другой на запад. Скорости их равны соответственно 10 км/ч и 24 км/ч. Какое расстояние (в километрах) будет между ними через 2 часа?

Решение:

Ответ: 52

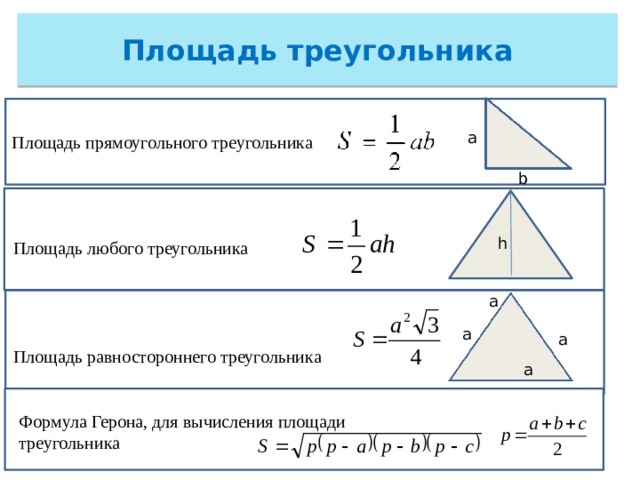
Площадь любого треугольника

Площадь равностороннего треугольника

Формула Герона, для вычисления площади треугольника

a

Площадь треугольника

Площадь прямоугольного треугольника

a

b

h

a

a

a

Гггггггггггггггггг

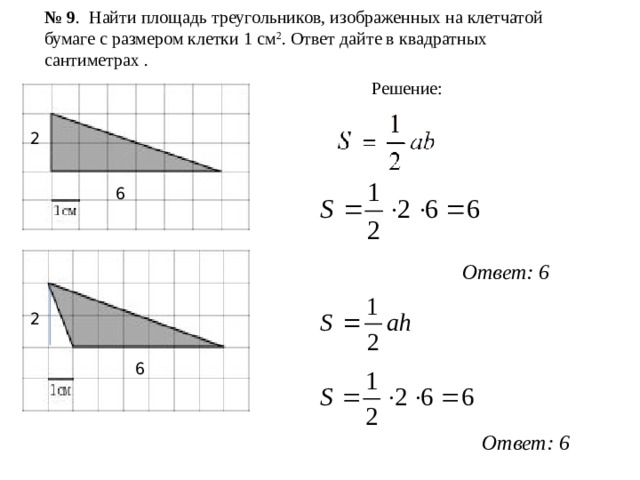
№ 9 . Найти площадь треугольников, изображенных на клетчатой бумаге с размером клетки 1 см 2 . Ответ дайте в квадратных сантиметрах .

Решение:

2

6

Ответ: 6

2

6

Ответ: 6

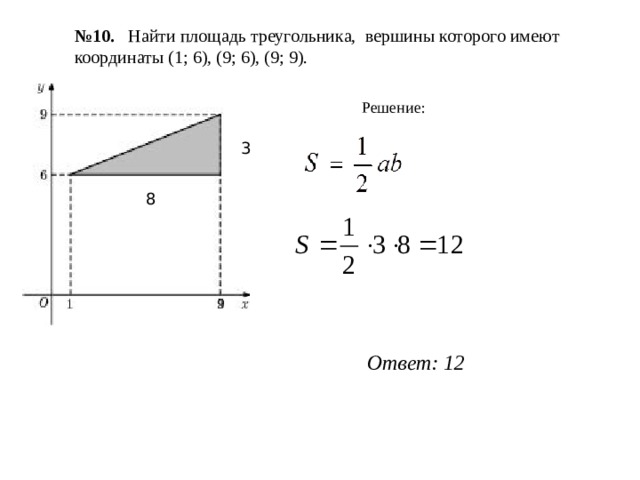
№ 10. Найти площадь треугольника, вершины которого имеют координаты (1; 6), (9; 6), (9; 9).

Решение:

3

8

Ответ: 12

№ 11 . Найти площадь треугольника, вершины которого имеют координаты (1; 6), (9; 6), (7; 9).

Решение:

3

8

Ответ: 12

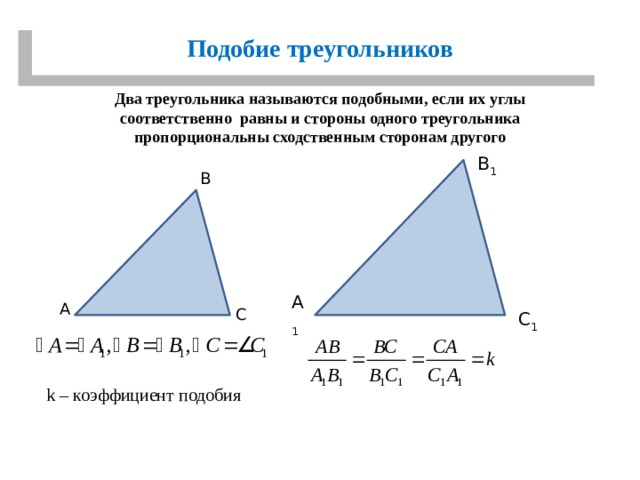
Подобие треугольников

Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого

В 1

В

А 1

А

С

С 1

k – коэффициент подобия

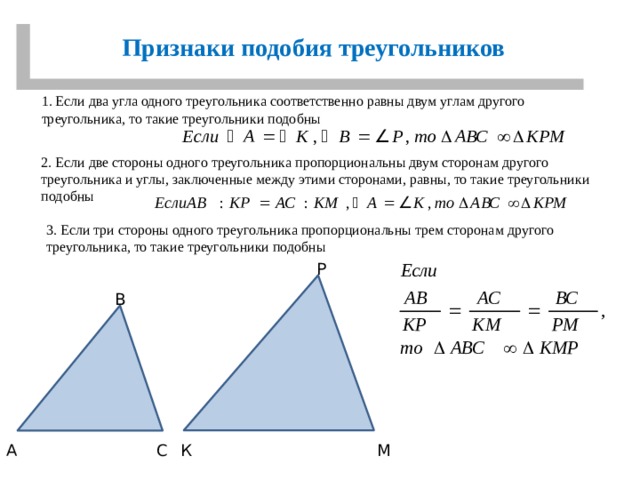
Признаки подобия треугольников

1. Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны

2. Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны

3. Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны

Р

В

С

К

М

А

∟ ABC – общий,

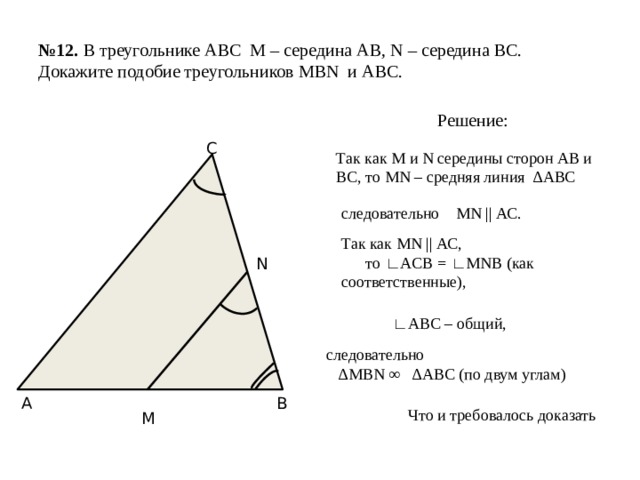
№ 12. В треугольнике АВС М – середина АВ, N – середина ВС. Докажите подобие треугольников MBN и ABC.

Решение:

С

Так как М и N середины сторон АВ и ВС, то MN – средняя линия ∆АВС

следовательно MN || АС.

Так как MN || АС,

то ∟ACB = ∟MNB (как соответственные),

N

следовательно

∆ MBN ∞ ∆ABC (по двум углам)

В

А

Что и требовалось доказать

М

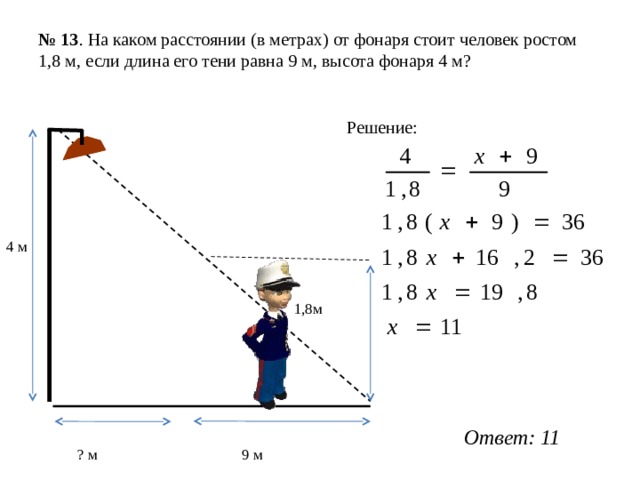
№ 13 . На каком расстоянии (в метрах) от фонаря стоит человек ростом 1,8 м, если длина его тени равна 9 м, высота фонаря 4 м?

4 м

1,8м

? м 9 м

Решение:

Ответ: 11

Домашнее задание:

№ 1.На каком расстоянии ( в метрах) от фонаря стоит человек ростом 2 м, если длина его тени равна 1 м, высота фонаря 9м?

№ 2.Один из внешних углов треугольника равен 15°. Углы не смежные с данным внешним углом, относятся как 1:4. Найдите наибольший из них. Ответ дайте в градусах.

№ 3.Найдите площадь прямоугольного треугольника, если гипотенуза равна 20, один из катетов 10, противолежащий ему угол равен 30°.

спасибо

За внимание!

Список источников основного содержания

• Геометрия :учебник для 7-9 классов для средней школы/ Л. С. Атанасян, В.Ф. Бутузов, С. Б. Кадомцев и др. – 2е изд.- Просвещение

2 . Основной Государственный экзамен, типовые варианты экзаменационных заданий/ И.Р.Высоцкий, Л.О.Рослова, Л.В.Кузнецова, и др, под ред. И.В. Ященко.- М. : Издательство «Экзамен», 2019.

Список источников иллюстраций

• Персонаж для презентации https://www.shutterstock.com/ru/search/%D0%BF%D0%B5%D1%80%D1%81%D0%BE%D0%BD%D0%B0%D0%B6+%D0%B4%D0%BB%D1%8F+%D0%BF%D1%80%D0%B5%D0%B7%D0%B5%D0%BD%D1%82%D0%B0%D1%86%D0%B8%D0%B8
• Телеграфные столбы

http://www.d-model.ru/image/cache/auhagen/auh44600-720x480.jpg

• Корабли:

• https://avatars.mds.yandex.net/get-pdb/1708639/995626e4-6c04-413e-a3e0-7feb0b47a54d/s1200