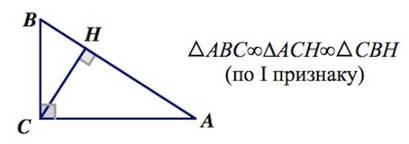Подобие треугольников. К ОГЭ

Подобные треугольники — треугольники, у которых углы соответственно равны, а стороны одного соответственно пропорциональны сторонам другого треугольника.

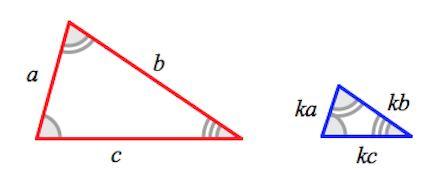
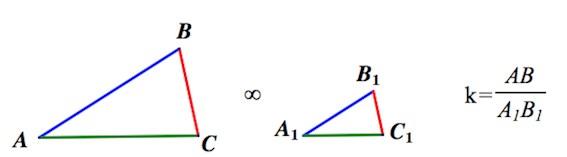
Коэффициентом подобия называют число k, равное отношению сходственных сторон подобных треугольников.

Сходственные (или соответственные) стороны  подобных треугольников — стороны, лежащие напротив равных углов.

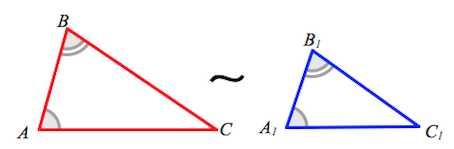
I признак подобия треугольников

Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.

 II признак подобия треугольников

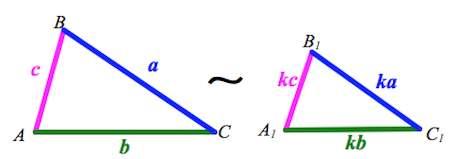
Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны.

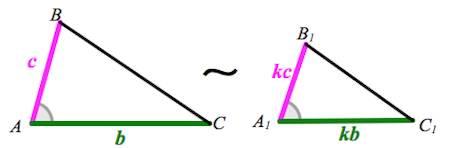
 III признак подобия треугольников

Если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны.

Признаки подобия прямоугольных треугольников:

1 Если прямоугольные треугольники имеют по равному острому углу, то такие треугольники подобны.

2. Если катеты одного прямоугольного треугольника пропорциональны катетам второго прямоугольного треугольника, то такие треугольники подобны.

3. Если катет и гипотенуза одного прямоугольного треугольника пропорциональны катету и гипотенузе второго прямоугольного треугольника, то такие треугольники подобны.

• Отношение площадей подобных треугольников равно квадрату коэффициента подобия.

• Отношение периметров подобных треугольников равно коэффициенту подобия.

• Отношение длин соответствующих элементов подобных треугольников (в частности,  длин биссектрис, медиан, высот и серединных перпендикуляров) равно коэффициенту подобия.

1. Прямая, параллельная стороне треугольника, отсекает от него треугольник, подобный данному.

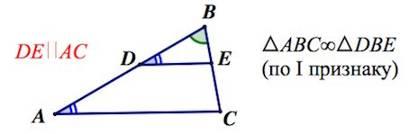
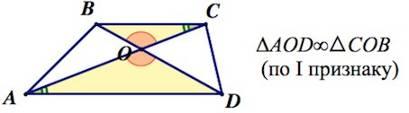
2. Треугольники   и , образованные отрезками диагоналей и основаниями трапеции, подобны. Коэффициент подобия – 

3. В прямоугольном треугольнике высота, проведенная из вершины прямого угла, разбивает его на два подобных треугольника, которые подобных исходному.

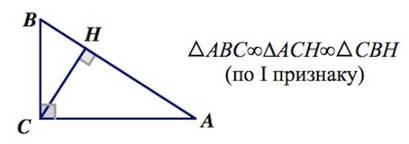
4.

Три средние линии треугольника делят его на четыре равных треугольника, подобные данному, с коэффициентом подобия ½:

Задачи из сборников по подготовке к ОГЭ №17

Задание 1  

Ко­рот­кое плечо шлаг­бау­ма имеет длину 1 м, а длин­ное плечо – 3 м. На какую вы­со­ту (в мет­рах) опу­стит­ся конец ко­рот­ко­го плеча, когда конец длин­но­го плеча под­ни­ма­ет­ся на 1,8м?

Задание 2 На каком рас­сто­я­нии (в мет­рах) от фо­на­ря стоит че­ло­век ро­стом 2 м, если длина его тени равна 1 м, вы­со­та фо­на­ря 9 м?

Задание 3 На каком рас­сто­я­нии (в мет­рах) от фо­на­ря стоит че­ло­век ро­стом 1,8 м, если длина его тени равна 9 м, вы­со­та фо­на­ря 4 м?

Задание 4

 Че­ло­век ро­стом 1,7 м стоит на рас­сто­я­нии 8 шагов от стол­ба, на ко­то­ром висит фо­нарь. Тень че­ло­ве­ка равна че­ты­рем шагам. На какой вы­со­те (в мет­рах) рас­по­ло­жен фо­нарь?

Задание 5 Про­ек­тор пол­но­стью осве­ща­ет экран A вы­со­той 80 см, рас­по­ло­жен­ный на рас­сто­я­нии 120 см от про­ек­то­ра. На каком наи­мень­шем рас­сто­я­нии (в сан­ти­мет­рах) от про­ек­то­ра нужно рас­по­ло­жить экран B вы­со­той 330 см, чтобы он был пол­но­стью освещён, если на­стройки про­ек­то­ра оста­ют­ся не­из­мен­ны­ми?