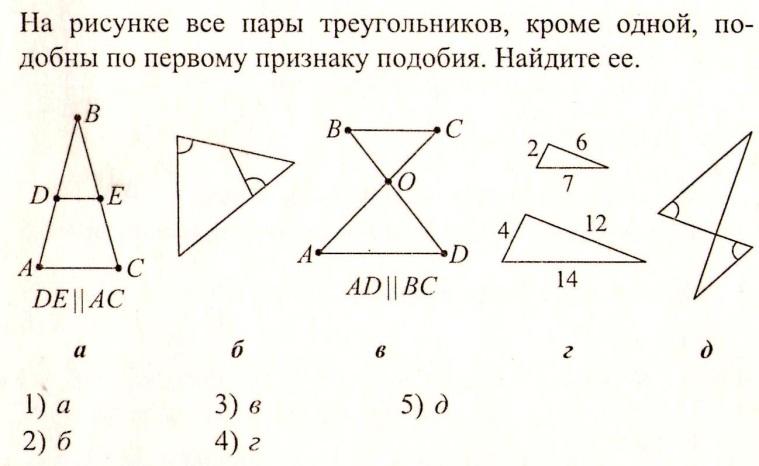
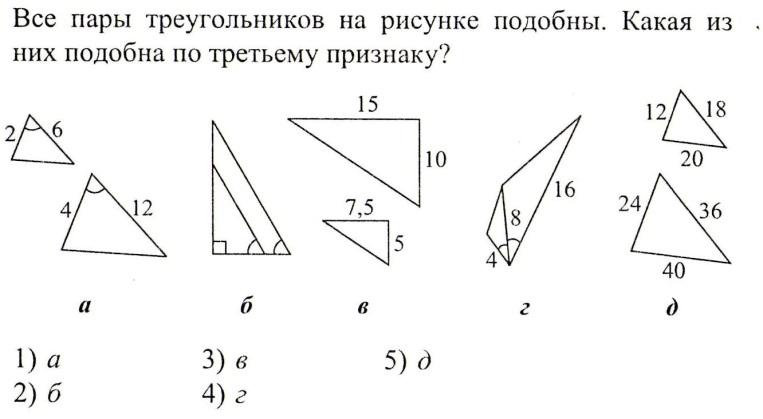
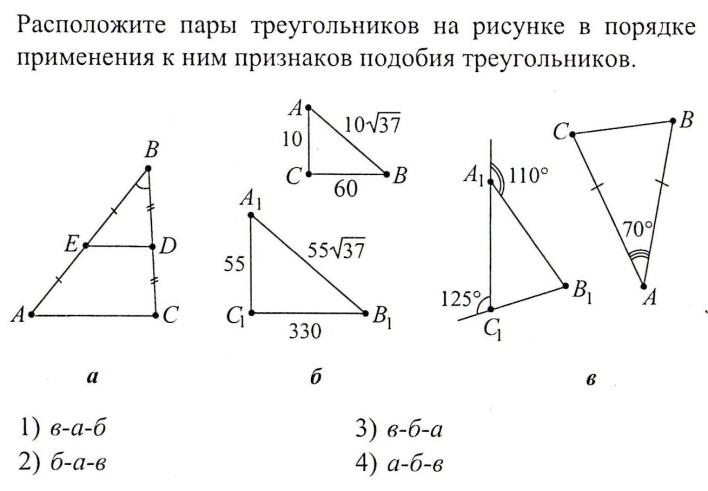
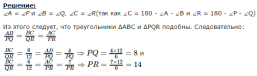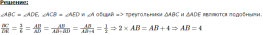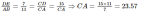Просмотр содержимого документа
«Решение задач по теме "Подобие треугольников"»
1. Через точки М и N, принадлежащие сторонам АВ и ВС треугольника ABC соответственно, проведена прямая МN, параллельная стороне АС. Найдите длину СN, если ВС = 6, МN = 4, АС = 9.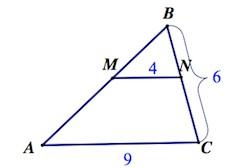
2. Прямая, параллельная основанию треугольника, делит его на треугольник и трапецию, площади которых относятся как 4:5. Периметр образовавшегося треугольника равен 20 см. Найдите периметр данного треугольника.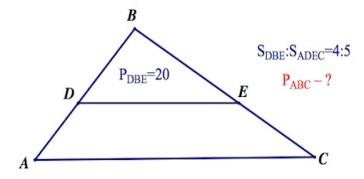
3. Через вершину прямого угла прямоугольного треугольника с катетами 6 и 8 см проведен перпендикуляр к гипотенузе. Вычислите площади образовавшихся треугольников.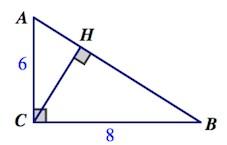
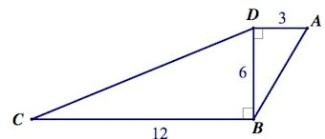
4. В трапеции ABCD меньшая диагональ BD, равная 6, перпендикулярна основаниям AD=3 и DC=12. Найдите сумму тупых углов B и D.
5. Основания трапеции равны a и b. Определите длину отрезка, параллельного основаниям и делящего трапецию на равновеликие части.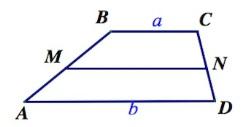
___________________________________________________________________
1. Через точки М и N, принадлежащие сторонам АВ и ВС треугольника ABC соответственно, проведена прямая МN, параллельная стороне АС. Найдите длину СN, если ВС = 6, МN = 4, АС = 9.
2. Прямая, параллельная основанию треугольника, делит его на треугольник и трапецию, площади которых относятся как 4:5. Периметр образовавшегося треугольника равен 20 см. Найдите периметр данного треугольника.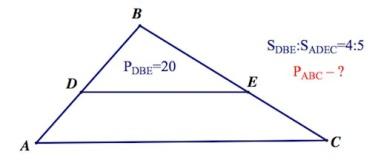
3. Через вершину прямого угла прямоугольного треугольника с катетами 6 и 8 см проведен перпендикуляр к гипотенузе. Вычислите площади образовавшихся треугольников.

4. В трапеции ABCD меньшая диагональ BD, равная 6, перпендикулярна основаниям AD=3 и DC=12. Найдите сумму тупых углов B и D.
5. Основания трапеции равны a и b. Определите длину отрезка, параллельного основаниям и делящего трапецию на равновеликие части.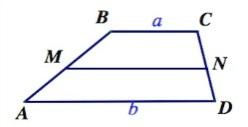
Задачи для изучения (с решением):
| Пример №1: Покажите, что два треугольника на рисунке внизу являются подобными.
Решение:
Так как длины сторон обоих треугольников известны, то здесь можно применить третий признак подобия треугольников: PQ/AB=6/2=3 QR/CB=12/4=3 PR/AC=15/5=3, Т.к. все отношения равны 3, то треугольники подобны | 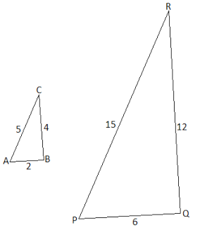
Третий признак подобия треугольников |
| Пример №2: Докажите, что два данных треугольника являются подобными и определите длины сторон PQ и PR. 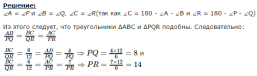
|
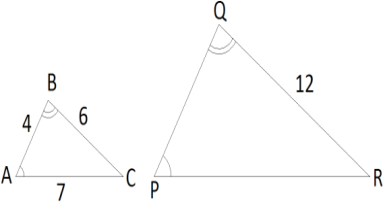
Первый признак подобия |
| Пример №3: Определите длину AB в данном треугольнике.
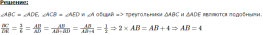
| 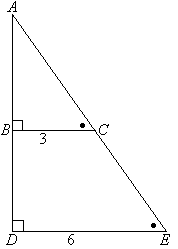
Первый признак подобия |
| Пример №4:Определить длину AD (x) геометрической фигуры на рисунке. Треугольники ΔABC и ΔCDE являются подобными так как AB || DE и у них общий верхний угол C.
Мы видим, что один треугольник является масштабированной версией другого. Однако нам нужно это доказать математически. AB || DE, CD || AC и BC || EC
∠BAC = ∠EDC и ∠ABC = ∠DEC Исходя из вышеизложенного и учитывая наличие общего угла C, мы можем утверждать, что треугольники ΔABC и ΔCDE подобны. Следовательно: 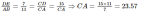 x = AC - DC = 23,57 - 15 = 8,57 | 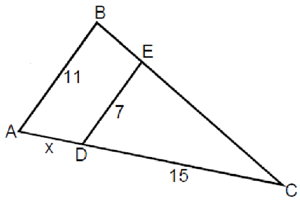
|
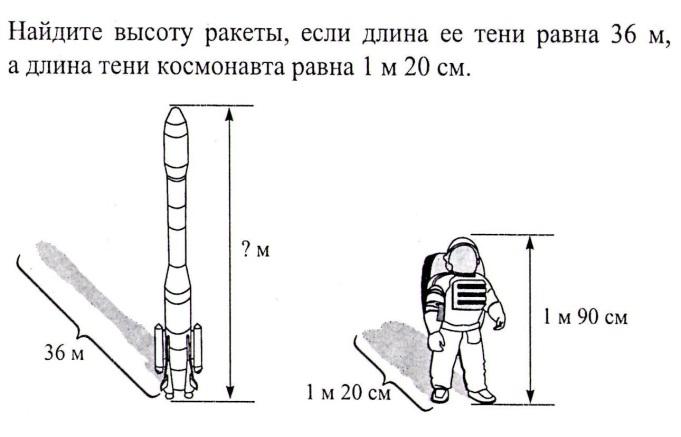
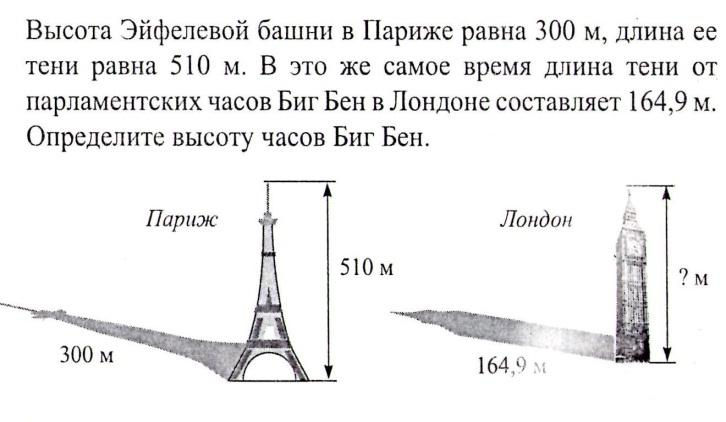
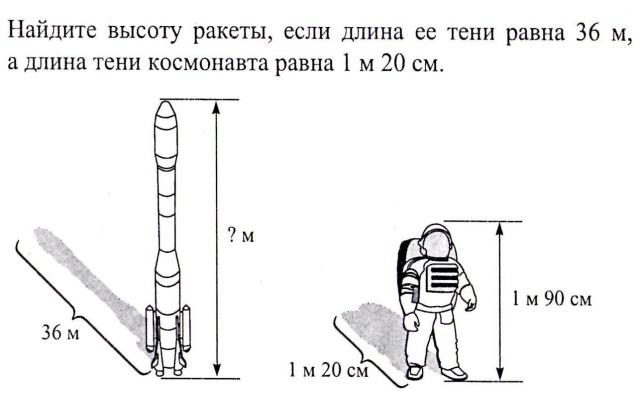
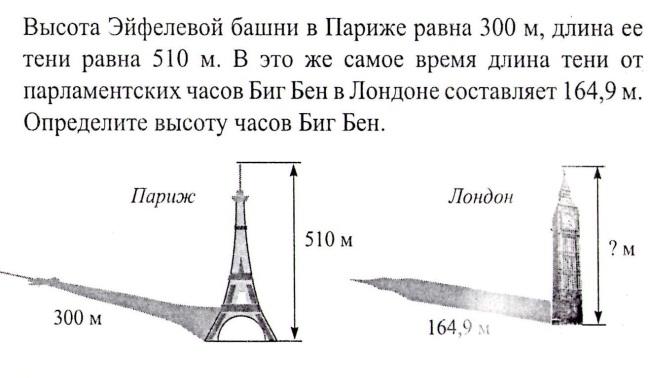
ТЕСТ