Россия, Советск
СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до 31.05.2025
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока
Была в сети 15.12.2024 23:13
Родич Валентина Григорьевна
Учитель математики
66 лет
7 490
6 248 
Местоположение
Специализация
Полуправильные многогранники
Категория:
Математика
28.01.2020 16:44
Просмотр содержимого документа
«Полуправильные многогранники»
Выполнила- учащаяся
10 «А» класса
Зайцева А.
Проверила- учитель математики Родич В.Г.
Полуправильные многогранники (Тела Архимеда).
Если гранями правильного многогранника или Платоновых тел являются однотипные правильные многоугольники (треугольники, квадраты и пентагоны), то гранями полуправильных многогранников, являются правильные многоугольники разных типов.
К полуправильным многогранникам относят n -угольные призмы, все ребра которых равны, а также антипризмы.
Кроме этих двух бесконечных серий полуправильных многогранников имеется 13 полуправильных многогранников, которые впервые открыл и описал Архимед, - это тела Архимеда.
Усеченный тетраэдр
Если срезать углы тетраэдра плоскостями, каждая из которых отсекает третью часть его ребер, выходящих из одной вершины, то получим усеченный тетраэдр, имеющий 8 граней. Из них 4 – правильные шестиугольники и 4 – правильные треугольники.
Усеченный октаэдр
Если указанным способом срезать вершины октаэдра, то получится усеченный октаэдр, имеющий 14 граней. 6 квадратов и 8 гексагонов.
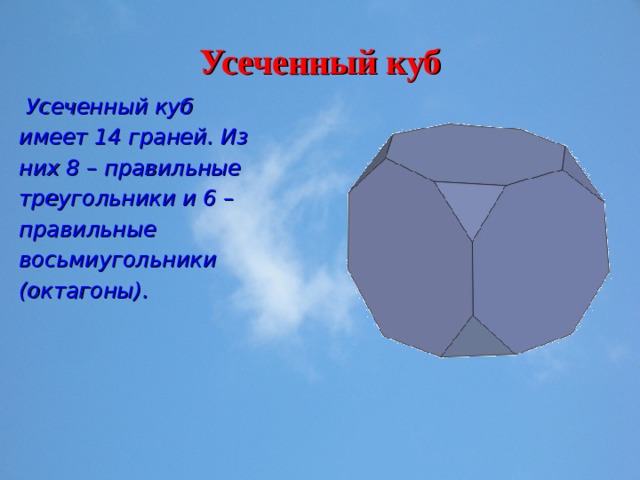
Усеченный куб
Усеченный куб имеет 14 граней. Из них 8 – правильные треугольники и 6 – правильные восьмиугольники (октагоны).
Усеченный икосаэдр
Усеченный икосаэдр имеет 32 грани. Из них 12 – правильные пятиугольники (пентагоны)
и 20 – правильные шестиугольники (гексагоны). Поверхность футбольного мяча изготавливают в форме поверхности усеченного икосаэдра
Усеченный додекаэдр
Усеченный додекаэдр имеет 32 грани. Из них 20 – правильные треугольники и 12 -правильные десятиугольники (декагоны).
Икосододекаэдр
Если в додекаэдре отсекающие плоскости провести через середины ребер, выходящих из одной вершины, то получим икосододекаэдр. У него 20 граней – правильные треугольники и 12 – правильные пятиугольники (пентагоны), то есть все грани икосаэдра и додекаэдра.
Ромбокубооктаэдр
Его поверхность состоит из граней куба и октаэдра, к которым добавлено еще 12 квадратов. Итого ромбокубооктаэдр имеет 8 треугольников и 18 квадратов .
Кубооктаэдр
Кубооктаэдр имеет 14 граней. Из них 8 треугольников и 6 квадратов.
Ромбоикосододекаэдр
Поверхность ромбоикосододекаэдра состоит из граней икосаэдра, додекаэдра и еще 30 квадратов. Итого он имеет 62 грани. Из них 20 треугольников, 30 квадратов и 12 пентагонов.
«Курносый» куб
Поверхность курносого куба состоит из граней куба окруженных правильными треугольниками. У него 38 граней. Из них 32 треугольника и 6 квадратов .
«Курносый» додекаэдр
Поверхность курносого додекаэдра из граней додекаэдра окруженных правильными треугольниками. 85 треугольников и 12 пентагонов.
Усеченный кубооктаэдр
Поверхность усеченного кубооктаэдра состоит из 12 квадратов, 8 правильных шестиугольников (гексагонов) и 6 правильных восьмиугольников (октагонов).
Усеченный икосододекаэдр
Поверхность усеченного икосододекаэдра состоит из 30 квадратов, 20 правильных шестиугольников (гексагонов) и 12 правильных десятиугольников (декагонов).
Новое «архимедово тело» - псевдоромбокубооктаэдр
Получается из ромбокубооктаэдра поворотом его верхней восьмиугольной «крышки» на 45 градусов по оси –
открыл Миллер в 1930 г. и независимо от него В. Г. Ашкинузе и Л. Есаулова.
- Кроме «архимедовых тел» к полуправильным многогранникам относятся все правильные n -угольные призмы , все ребра которых равны.
- К полуправильным многогранникам относятся также все так называемые антипризмы.
© 2020, Родич Валентина Григорьевна 479 3
Рекомендуем курсы ПК и ППК для учителей
Похожие файлы
Вебинар для учителей
Свидетельство об участии БЕСПЛАТНО!
Полезное для учителя
Реализация образовательных программ осуществляется с применением исключительно электронного обучения и ДОТ
