Понятие линейной функции и ее график

Открытый урок по теме: «Понятие линейной функции и ее график»

Тип урока: урок изучения нового материала.

Наглядное пособие: презентация к уроку.

Цели урока:

образовательные:

• сформулировать определение линейной функции;

• сформировать представление о графике линейной функции;

• выявить роль параметров b и k в расположении графика линейной функции;

• формировать умение строить график линейной функции;

развивающие:

• развитее умения анализировать, обобщать, делать выводы;

• развитие логического мышления;

воспитывающие:

• воспитание активности,

• формирование навыков самостоятельной работы,

• формирование взаимоконтроля, самоконтроля деятельности;

• формирование интереса к предмету.

План урока:

1. Организационный момент

2. Актуализация опорных знаний

3. Изучение нового материала

4. Первичное осмысление изученного

5. Постановка домашнего задания

6. Подведение итогов урока

Ход урока.

1. Организационный момент

Приветствие учеников. Проверка присутствующих. Сообщение темы урока. Постановка целей урока.

1. Актуализация опорных знаний

1. Фронтальный опрос:

1. Дайте определение функции?

2. Определение функции прямой пропорциональности?

3. Что является график прямой пропорциональности?

4. От чего зависит в каких четвертях располагается график?

5. Сколько точек необходимо, чтобы построить график функции y=kx?

1. Самостоятельная работа (Слайд 3-5)

С одного ряда работы сдаются учителю, остальные выполняют взаимопроверку (Слайд 6)

1. Изучение нового материала

1. Совместно с учениками рассмотреть примеры в учебнике (пункт16, пример 1,2) и сформулировать определение линейной функции (Слайд 7).

2. № 316 (Слайд 8-9) письменно с комментариями с места.

Указать для линейных функций коэффициент k и b

1. Сообщить, что графиком линейной функции является прямая (Слайд 10). И расположение ее зависит от коэффициентов k и b.

2. Теперь задача сводится к рассмотрению всевозможных случаев. (Слайд 11)

Все случаи рассматриваются при непосредственном участии учеников и работе их у доски:

1. Случай, когда b=0 , k ≠0 (у доски 1 человек). Здесь линейная функция превращается в прямую пропорциональность, а значит график ее проходит через начало координат и расположение по четвертям зависит от знака коэффициента прямой пропорциональности (Слайды 12-13).

2. Случаи, когда k=0 (у доски 1 человек). (Слайды 14- 16)

3. Теперь 2 ученика работают на закрытых досках по вариантам, остальные в тетради:

1. вариант – строят графики функций: y= 2x+1 и y=2x-1 (Слайд 17)

2. вариант – строят графики функций: y= -2x+1 и y= -2x-1 (Слайд 18)

1. Сравнив 3 графика из первой строки и 3 графика из второй строки, можно сделать вывод, что график линейной функции y=kx+b получается из графика прямой пропорциональности y=kx путем смещения по оси OY на b единиц (ниже ОХ, если bb0), а зависимость расположения графиков от k такая же, как и у прямой пропорциональности (k0 – I, III четверти, kII, IV четверти).

Т. о можно составить следующий алгоритм построения графика линейной функции:

а) по уравнению определяем, как выглядит график (параллельно или нет оси ОХ, проходит через начало координат или нет) и в каких четвертях лежит;

б) строим, если необходимо таблицу из 2-3 (для проверки) точек, вычисляем по формуле значения;

в) отмечаем полученные точки на координатной плоскости;

г) проводим через отмеченные точки прямую (подписываем).

1. Первичное осмысление изученного.

(Слайд 19) Что является графиком функции и как он расположен?

№ 319 (а,б,д)

1. Постановка домашнего задания. (Слайд 20)

№ 314, 318, 320, 336(а) – на повторение темы «Решение уравнений»

1. Подведение итогов урока (Слайд 21)

1. Дайте определение линейной функции?

2. Что является графиком линейной функции?

3. Как влияют параметры k и b на расположение графика линейной функции?

4. Каков алгоритм построения графика линейной функции?

5. Дополнительное задание: (Слайд 22- 26). Найдите ошибку.

6. Выставление оценок за урок.

Используемая литература:

1. Алгебра.7 класс: учебник для общеобраз.учреждений/ [Ю.Н. Макарычев, и др.]; под ред. С.А.Теляковского.– М.: Просвещение,2009

2. Алгебра. 7 класс: поурочные планы по учебнику Ю.Н. Макарычева и др./Т.Ю. Дюмина, А.А. Махонина.– Волгоград: Учитель, 2011.

Линейная функция и ее график

7 класс.

Зубков Александр Геннадьевич

МКОУ Карайчевская ООШ

Цели урока :

• сформулировать определение линейной функции, представление о ее графике;
• выявить роль параметров b и k в расположении графика линейной функции;
• формировать умение строить график линейной функции;
• развитее умения анализировать, обобщать, делать выводы; развитие логического мышления;
• формирование навыков самостоятельной деятельности, взаимоконтроля, самоконтроля

1. Какие из функций являются прямой пропорциональностью.

1 вариант

а) y= 13x

б) y=

в) y =

2 вариант

а) y= -7x

б) y=

в) y =

2 . В каких координатных четвертях проходит график функции

2 вариант

а) у= -7,8х

б) y=

1 вариант

а ) y= 50x

б) y= -

3. Постройте график функции

1 вариант

2 вариант

y= - 1,5x

y= 0,5x

(за единицу взять 2 клетки)

(за единицу взять 2 клетки )

Ответы

2 вариант

• 1. а; в
• 2. а) 2; 4 б) 1; 3
• 3.

1 вариант

• 1. а; б
• 2. а) 1; 3 б) 2; 4
• 3.

y

y

1

1

0

х

2

1

0

х

1

2

-3

Линейная функция

Функция , которую можно задать формулой вида y = kx + b ,

где x – независимая переменная, k, b - некоторые числа

№ 316

a) y=2x-3

линейная функция, k=2

б)y=7-9x

y=-9x+7

линейная функция, k=-9

линейная функция, k=

функция нелинейная т.к. x в знаменателе

функция нелинейная т.к. x в квадрате

линейная функция, k=2

Графиком линейной функции является прямая .

0 K0 bKb=0 K=0" width="640"

Зависимость графика линейной функции от k и b

b

k

b0

K0

b

K

b=0

K=0

0 K0 Kbb=0 K=0 y=kx I, III четверти Через начало коорд y x 0" width="640"

b

k

b0

K0

K

b

b=0

K=0

y=kx I, III четверти

Через начало коорд

y

x

0

0 K0 KbK=0 b=0 y=kx I, III четверти y=kx II, IV четверти Через начало коорд Через начало коорд y x 0 y x 0" width="640"

b

k

b0

K0

K

b

K=0

b=0

y=kx I, III четверти

y=kx II, IV четверти

Через начало коорд

Через начало коорд

y

x

0

y

x

0

0 b0 KbK=0 b=0 y=kx I, III четверти y=kx II, IV четверти Через начало коорд Через начало коорд y=0 Cовпадает с ох y x 0 y x 0 y x 0" width="640"

b

k

K0

b0

K

b

K=0

b=0

y=kx I, III четверти

y=kx II, IV четверти

Через начало коорд

Через начало коорд

y=0 Cовпадает с ох

y

x

0

y

x

0

y

x

0

0 b0 KbK=0 b=0 y=kx I, III четверти y=kx II, IV четверти Через начало коорд y=b ; II ox Через начало коорд y=0 Cовпадает с ох ниже оx (3,4 четверти) y x 0 y x 0 y y x 0 0 x" width="640"

b

k

K0

b0

K

b

K=0

b=0

y=kx I, III четверти

y=kx II, IV четверти

Через начало коорд

y=b ; II ox

Через начало коорд

y=0 Cовпадает с ох

ниже оx (3,4 четверти)

y

x

0

y

x

0

y

y

x

0

0

x

0 k b0 KbK=0 b=0 y=b ; II ox y=kx I, III четверти Через начало коорд y=kx II, IV четверти выше оx (1,2 четверти) y=b ; II ox Через начало коорд ниже оx (3,4 четверти) y=0 совпадает с ох y x 0 y x 0 y y y x 0 0 x x 0" width="640"

b

K0

k

b0

K

b

K=0

b=0

y=b ; II ox

y=kx I, III четверти

Через начало коорд

y=kx II, IV четверти

выше оx (1,2 четверти)

y=b ; II ox

Через начало коорд

ниже оx (3,4 четверти)

y=0 совпадает с ох

y

x

0

y

x

0

y

y

y

x

0

0

x

x

0

0 k b0 y=kx+b (y=2x + 1) Kb b=0 K=0 y=kx+b (y=2x - 1) y=kx I, III четверти y=b ; (y= 2) II ox выше оx (1,2 четверти) y=kx II, IV четверти Через начало коорд y=b ; (y= - 2) II ox I, III четверти Через начало коорд ниже оx (3,4 четверти) y=0 совпадает с ох I, III четверти y y y x 0 x 0 x 0 x y x 0 y y y 0 x 0 x 0 0 x 0" width="640"

b

K0

k

b0

y=kx+b (y=2x + 1)

K

b

b=0

K=0

y=kx+b (y=2x - 1)

y=kx I, III четверти

y=b ; (y= 2) II ox

выше оx (1,2 четверти)

y=kx II, IV четверти

Через начало коорд

y=b ; (y= - 2) II ox

I, III четверти

Через начало коорд

ниже оx (3,4 четверти)

y=0 совпадает с ох

I, III четверти

y

y

y

x

0

x

0

x

0

x

y

x

0

y

y

y

0

x

0

x

0

0

x

0

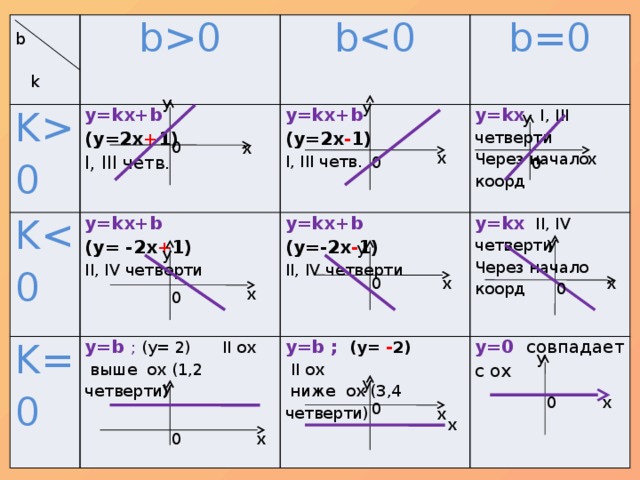0 b0 Ky=kx+b (y=2x + 1) bI, III четв. y=kx+b (y= -2x + 1) y=kx+b (y=2x - 1) K=0 b=0 II, IV четверти y=kx+b (y=-2x - 1) y=kx I, III четверти I, III четв. y=b ; (y= 2) II ox II, IV четверти выше оx (1,2 четверти) y=kx II, IV четверти Через начало коорд y=b ; (y= - 2) II ox Через начало коорд y=0 совпадает с ох ниже оx (3,4 четверти) y y y 0 x x x 0 0 y y y x 0 x 0 x 0 y y y 0 x 0 x x x 0" width="640"

b

k

K0

b0

K

y=kx+b (y=2x + 1)

b

I, III четв.

y=kx+b (y= -2x + 1)

y=kx+b (y=2x - 1)

K=0

b=0

II, IV четверти

y=kx+b (y=-2x - 1)

y=kx I, III четверти

I, III четв.

y=b ; (y= 2) II ox

II, IV четверти

выше оx (1,2 четверти)

y=kx II, IV четверти

Через начало коорд

y=b ; (y= - 2) II ox

Через начало коорд

y=0 совпадает с ох

ниже оx (3,4 четверти)

y

y

y

0

x

x

x

0

0

y

y

y

x

0

x

0

x

0

y

y

y

0

x

0

x

x

x

0

Что является графиком функции и как он расположен?

а) y= -3x + 5

б) y= x

в) y= -3

г) y=

д) y=

е) y= 0

Домашнее задание .

№ 314, 318, 320,

№ 336(а)-на повторение темы «Решение уравнений»

Итоги урока:

Подведение итогов урока

• Дайте определение линейной функции?
• Что является графиком линейной функции?
• Как влияют параметры k и b на расположение графика линейной функции?
• Каков алгоритм построения графика линейной функции?

Найдите ошибку:

y = 2x

Верно

y

y

y = 2

y = 2x

1

1

х

х

0

0

1

1

Найдите ошибку:

y = x +1

y = x+1

y = 2x

Верно

y

y

1

1

х

х

0

0

1

1

Найдите ошибку:

y = x - 2

y = x+2

y = x - 2

Верно

y

y

1

1

х

х

0

0

1

1

Найдите ошибку:

y = -3x

y =3x

y = -3x

Верно

y

y

1

1

х

х

0

0

1

1

Найдите ошибку:

y = 1-x

y = x-1

y = 1-x

Верно

y

y

1

1

х

х

0

0

1

1

Используемая литература:

1. Алгебра.7 класс: учебник для общеобраз.учреждений/ [Ю.Н. Макарычев, и др. ] ; под ред. С.А.Теляковского.- М.: Просвещение,2009

2. Алгебра. 7 класс: поурочные планы по учебнику Ю.Н. Макарычева и др./Т.Ю. Дюмина, А.А. Махонина.- Волгоград: Учитель, 2011.

Подготовил:

Зубков Александр Геннадьевич

учитель математики

МКОУ Карайчевская ООШ

Бутурлиновского муниципального района