Построение сечений параллелепипеда и тетраэдра

Построение сечений тетраэдра и параллелепипеда

Содержание:

• Цели и задачи
• Введение
• Понятие секущей плоскости
• Определение сечения
• Правила построения сечений
• Виды сечений тетраэдра
• Виды сечений параллелепипеда
• Задача на построение сечения тетраэдра с объяснением
• Задача на построение сечения тетраэдра с объяснением
• Задача на построение сечения тетраэдра по наводящим вопросам
• Второй вариант решения предыдущей задачи
• Задача на построение сечения параллелепипеда
• Задача на построение сечения параллелепипеда
• Источники информации
• Пожелание учащимся

Цель работы:

Развитие пространственных представлений у учащихся.

Задачи:

• Познакомить с правилами построения сечений.
• Выработать навыки построения сечений тетраэдра и параллелепипеда при различных случаях задания секущей плоскости.
• Сформировать умение применять правила построения сечений при решении задач по темам «Многогранники».

Для решения многих геометрических задач необходимо строить их сечения различными плоскостями.

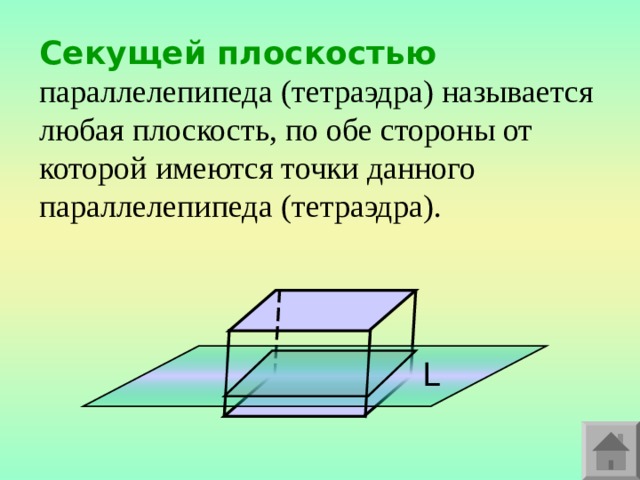
Секущей плоскостью параллелепипеда ( тетраэдра) называется любая плоскость, по обе стороны от которой имеются точки данного параллелепипеда (тетраэдра).

L

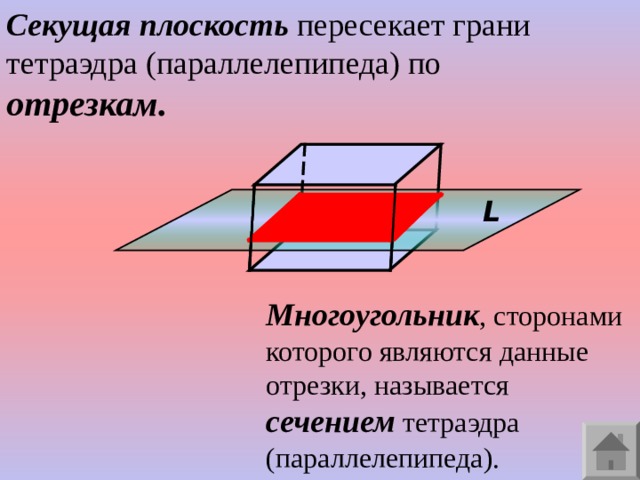
Секущая плоскость пересекает грани тетраэдра (параллелепипеда) по отрезкам.

L

Многоугольник , сторонами которого являются данные отрезки, называется сечением тетраэдра (параллелепипеда).

Для построения сечения нужно построить точки пересечения секущей плоскости с ребрами и соединить их отрезками.

При этом необходимо учитывать следующее:

1. Соединять можно только две точки, лежащие

в плоскости одной грани.

2. Секущая плоскость пересекает параллельные грани по параллельным отрезкам.

3. Если в плоскости грани отмечена только одна точка, принадлежащая плоскости сечения, то надо построить дополнительную точку. Для этого необходимо найти точки пересечения уже построенных прямых с другими прямыми, лежащими в тех же гранях.

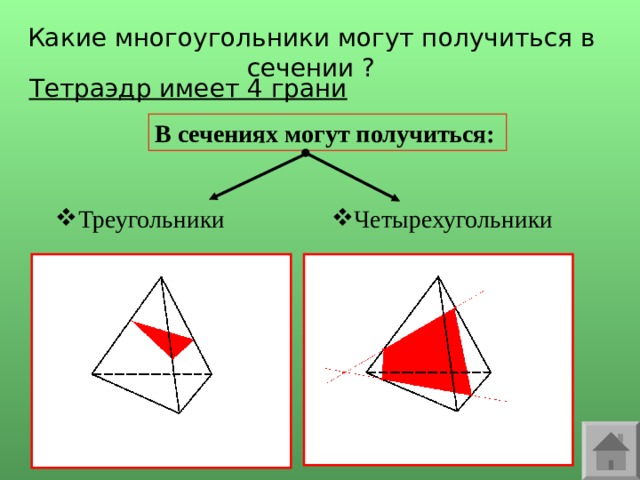
Какие многоугольники могут получиться в сечении ?

Тетраэдр имеет 4 грани

В сечениях могут получиться:

• Четырехугольники

• Треугольники

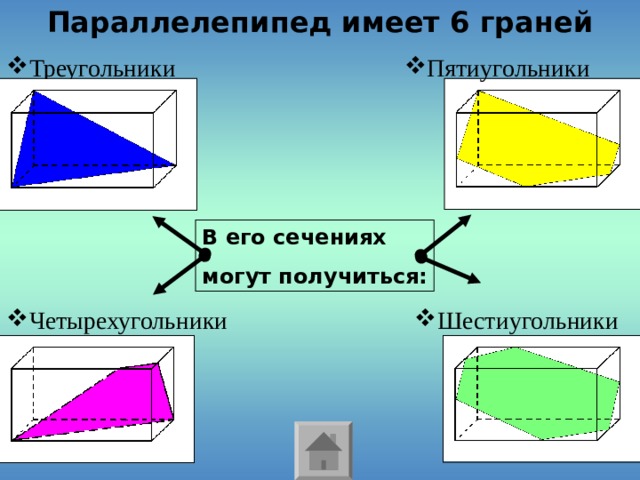
Параллелепипед имеет 6 граней

• Треугольники

• Пятиугольники

В его сечениях

могут получиться:

• Четырехугольники

• Шестиугольники

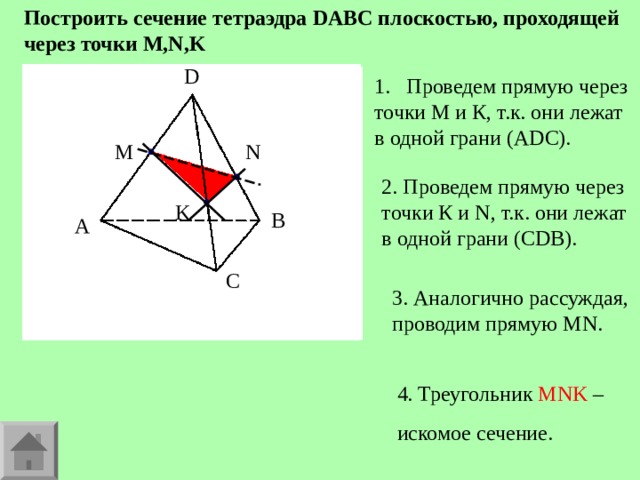
Построить сечение тетраэдра DABC плоскостью, проходящей через точки M , N , K

D

D

• Проведем прямую через

точки М и К, т.к. они лежат

в одной грани (А DC ).

M

N

2. Проведем прямую через точки К и N , т.к. они лежат в одной грани (С DB ).

K

B

A

B

A

C

C

3. Аналогично рассуждая, проводим прямую MN .

4. Треугольник MNK –

искомое сечение.

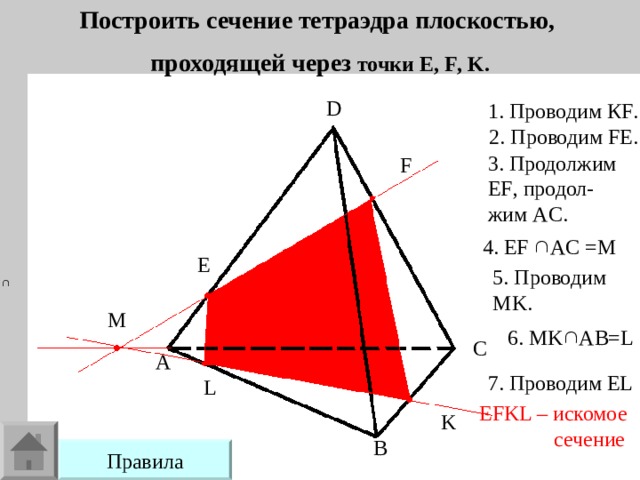
Построить сечение тетраэдра плоскостью,

проходящей через точки E , F , K .

D

1. Проводим К F .

2. Проводим FE .

3. Продолжим EF , продол- жим AC .

F

4. EF AC = М

E

5. Проводим MK .

M

6. MK AB=L

C

A

7. Проводим EL

L

EFKL – искомое

сечение

K

B

Правила

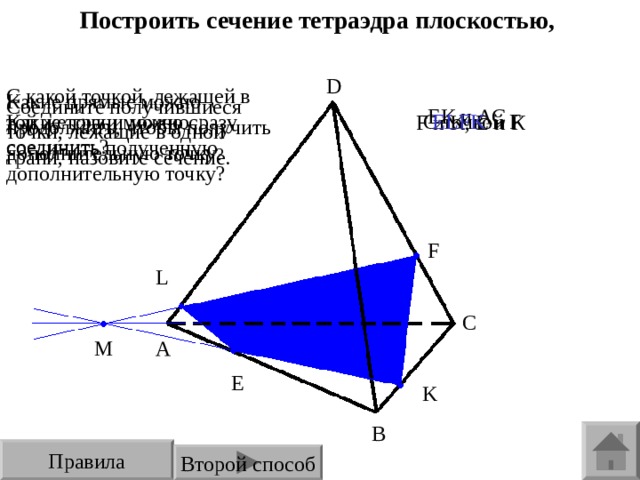
Построить сечение тетраэдра плоскостью,

проходящей через точки E , F , K .

D

С какой точкой, лежащей в той же грани можно соединить полученную дополнительную точку?

Какие прямые можно продолжить, чтобы получить дополнительную точку ?

Соедините получившиеся точки, лежащие в одной грани, назовите сечение.

ЕК и АС

Е LFK

С точкой F

Какие точки можно сразу соединить?

F и K , Е и К

F

L

C

M

A

E

K

B

Правила

Второй способ

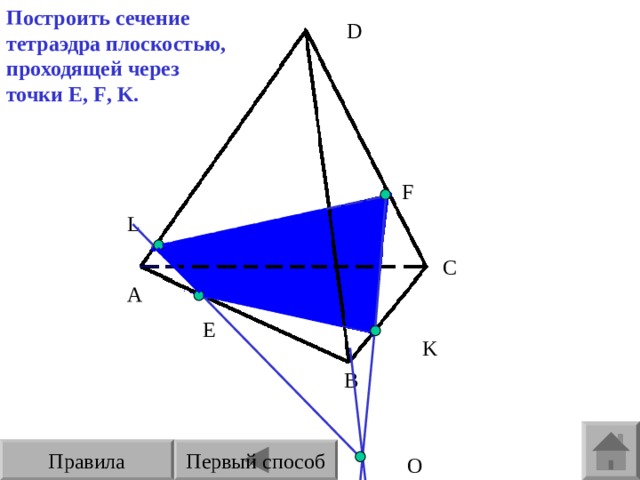
Построить сечение тетраэдра плоскостью,

проходящей через точки E , F , K .

D

F

L

C

A

E

K

B

Правила

Первый способ

О

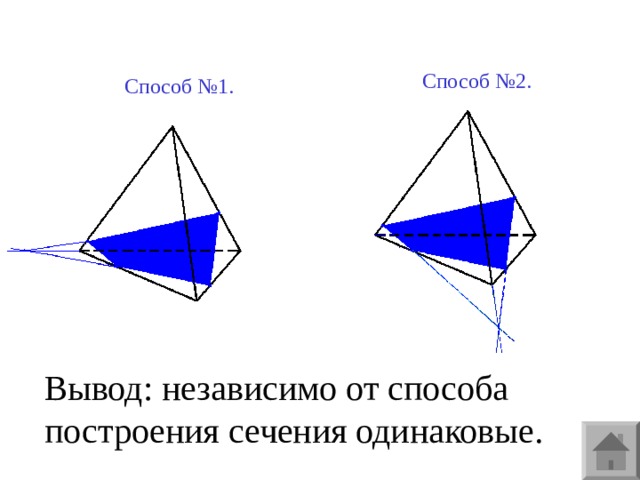
Способ №2.

Способ №1.

Вывод: независимо от способа построения сечения одинаковые.

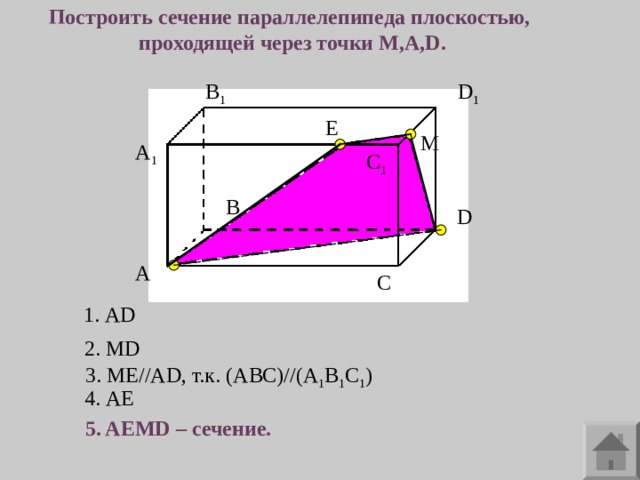
Построить сечение параллелепипеда плоскостью,

проходящей через точки M,A,D.

В 1

D 1

E

М

A 1

С 1

В

D

А

С

1. AD

2. MD

3. ME//AD , т.к. ( ABC)//(A 1 B 1 C 1 )

4. AE

5. AEMD – сечение.

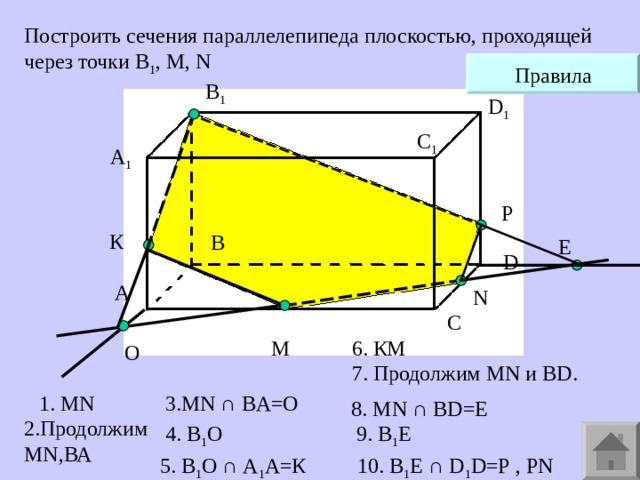
Построить сечения параллелепипеда плоскостью, проходящей через точки В 1 , М, N

Правила

В 1

D 1

С 1

A 1

P

К

В

Е

D

А

N

С

M

6. КМ

O

7. Продолжим MN и BD .

1. MN

3. MN ∩ BA=O

8 . MN ∩ BD=E

2.Продолжим MN ,ВА

4. В 1 О

9. В 1 E

5. В 1 О ∩ А 1 А=К

10. B 1 Е ∩ D 1 D=P , PN

Источники информации

• 1. Геометрия 10-11: учебник для общеобразоват. учреждений / Л.С.Атанасян, В.Ф.Бутузов и др.,М.Просвещение
• 2. Задачи к урокам геометрии 7-11 классы / Б.Г.Зив,С.-Петербург, НПО «Мир и семья», изд-во «Акация».
• 3. Математика: Большой справочник для школьников и поступающих в ВУЗы / Д.И.Аверьянов, П.И.Алтынов – М.: Дрофа

ВЫ МНОГОЕ УЗНАЛИ

И МНОГОЕ УВИДЕЛИ!

ТАК ВПЕРЕД, РЕБЯТА:

ДЕРЗАЙТЕ И ТВОРИТЕ!

СПАСИБО ЗА ВНИМАНИЕ.