Россия, Певек
СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока
Была в сети 12.10.2019 11:26
Вестман Ольга Николаевна
учитель информатики
71 год
23 950
1 184 
Местоположение
Специализация
Построение таблиц истинности (презентация к уроку)
Категория:
Информатика
20.02.2015 07:50
Просмотр содержимого документа
«Построение таблиц истинности (презентация к уроку)»
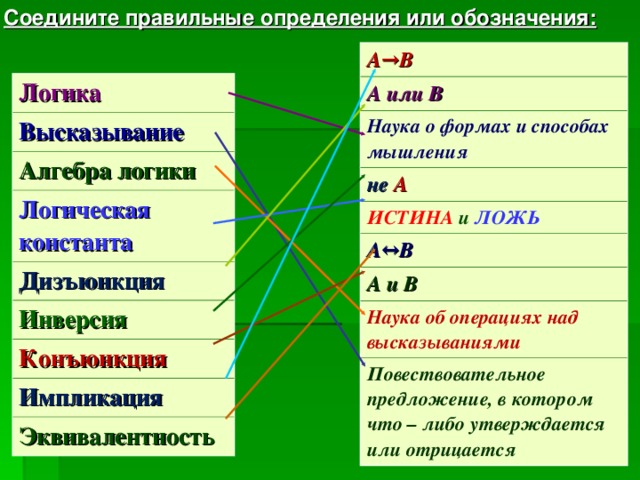
Соедините правильные определения или обозначения:
А →В
А или В
Наука о формах и способах мышления
не А
ИСТИНА и ЛОЖЬ
А ↔В
А и В
Наука об операциях над высказываниями
Повествовательное предложение, в котором что – либо утверждается или отрицается
Логика
Высказывание
Алгебра логики
Логическая константа
Дизъюнкция
Инверсия
Конъюнкция
Импликация
Эквивалентность
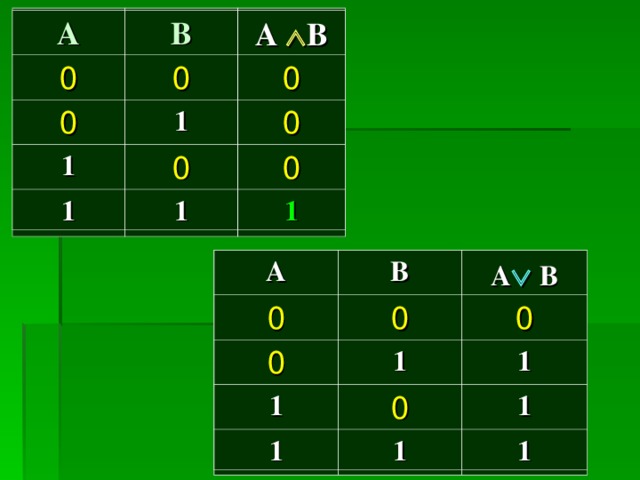
А
В
А В
А
0
В
0
А В
0
0
1
1
1
0
0
0
1
1
А
А
0
В
В
А В
0
0
А В
0
1
1
1
1
0
1
1
1
А
А
В
В
0
А В
А В
0
0
0
1
1
0
1
1
1
1
0
А
А
0
В
В
0
0
А В
А В
1
1
1
1
1
0
0
1
1
А
А
В
0
В
0
0
А В
А В
1
1
1
0
1
0
0
1
1
А
А
0
не А
не А
1
1
0
Таблицы истинности
Всякое сложное высказывание принимает значение 1 или 0 в зависимости от значения простых высказываний , из которых оно построено.
Таблицу , показывающую, какие значения принимает сложное высказывание при всех сочетаниях ( наборах ) значений входящих в него простых высказываний , называют таблицей истинности сложного высказывания.
A
0
B
0
0
F
1
1
1
1
1
0
1
1
0
Алгоритм построения таблиц истинности( ТИ )
- Подсчитать n – количество переменных в формуле
- Определить число строк в таблице m =2 n
- Подсчитать количество логических операций в формуле, установив порядок действий
- Определить количество столбцов в таблице:
число переменных + число операций
5. Выписать наборы входных переменных и провести заполнение ТИ по столбцам
(5) (4) (1) (3) (2)
ПРИМЕР 1. Для формулы A *( B + не B * не C )
построить таблицу истинности
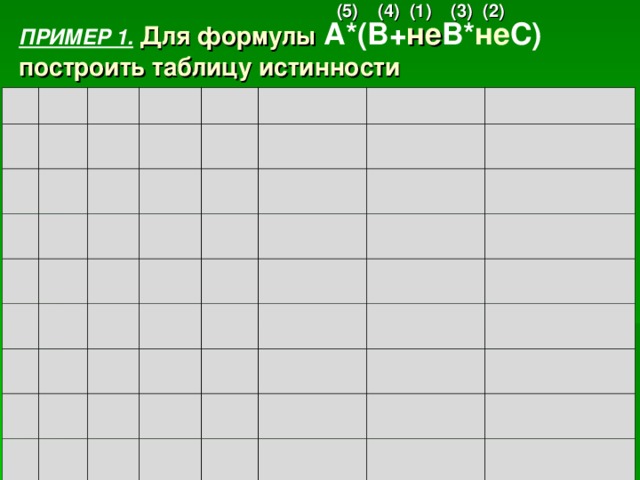
(5) (4) (1) (3) (2)
ПРИМЕР 1. Для формулы A *( B + не B * не C )
построить таблицу истинности
ПРИМЕР 1. Для формулы A *( B + не B * не C )
построить таблицу истинности
(5) (4) (1) (3) (2)
A
0
B
0
C
0
0
не B
0
0
1
1
не C
0
1
1
0
1
1
не B *не C
1
0
1
0
0
1
1
0
0
1
0
0
1
B + не B* не C
1
0
1
A * (B + не B *не C)
1
0
1
1
0
0
1
1
1
0
0
1
0
1
0
0
1
0
1
0
1
0
1
0
0
1
0
0
0
1
0
1
1
1
4
5
2
3
1
В классе
- B+( не B*A)
- A*(B+ не B*C)
3. (A+B)*C не A*B
4. A*B*C+( не B*C+A)
5. A*B*C ↔ ( не B*C+A)
1. B+( не B*A)
1. B+ не B*A
A
B
0
не B
0
0
не B*A
1
1
1
1
0
0
0
B+ не B*A
0
0
1
1
1
1
0
1
0
1
2. A*(B+ не B*C)
2. A*(B+ не B*C)
A
B
0
0
C
0
не B
0
0
0
1
не B*C
1
1
0
B+ не B*C
0
1
1
0
1
1
0
A*(B+ не B*C)
0
1
1
0
1
0
1
0
0
0
0
0
0
1
1
1
1
1
1
0
0
1
0
1
0
0
0
1
1
1
0
0
0
0
1
1
1
1
1
3. (A+B)*C не A*B
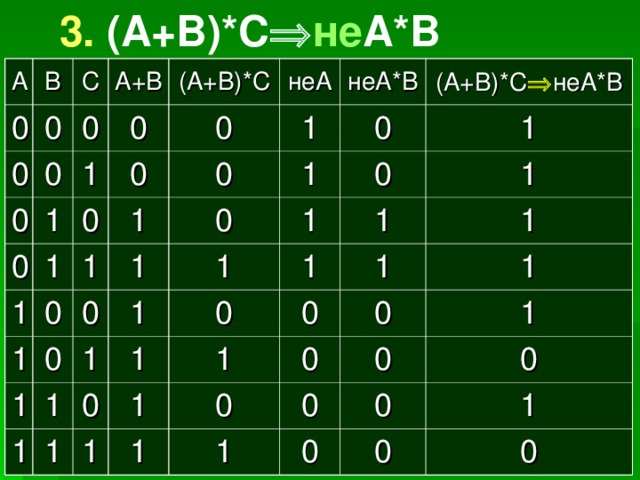
3. (A+B)*C не A*B
A
0
B
C
0
0
0
A+B
0
0
(A+B)*C
0
0
1
1
не A
0
1
0
0
1
1
не A*B
0
1
1
0
1
(A+B)*C не A*B
0
0
0
1
1
1
0
1
1
1
1
1
1
0
1
1
0
1
0
1
1
1
1
1
1
0
1
1
0
1
0
0
1
0
0
1
1
0
0
0
1
0
0
4. A*B*C+( не B*C+A)
4. A*B*C+( не B*C+A)
A
0
B
C
0
0
0
A*B*C
0
0
не B
0
0
1
1
не B*C
1
1
0
0
1
0
не B*C +A
1
1
0
0
1
A*B*C+( не B*C+A)
0
0
0
1
0
1
0
0
1
1
0
1
0
1
0
1
0
0
1
0
0
1
0
1
0
0
0
1
0
1
1
1
0
0
1
1
0
1
1
0
1
1
1
5. A*B*C ↔ ( не B*C+A)
5. A*B*C ↔ ( не B*C+A)
A
0
B
C
0
0
0
A*B*C
0
0
не B
0
0
1
1
не B*C
1
1
0
0
1
0
не B*C +A
1
1
0
0
1
A*B*C ↔ ( не B*C+A)
0
0
0
1
0
1
0
1
1
1
0
1
0
1
0
1
0
0
1
0
0
0
1
1
0
0
0
1
0
1
1
1
1
0
1
0
0
0
1
0
0
1
1
Самостоятельно:
Для формул построить ТИ
- A *( не A + B + C )
- (A → B) ↔ (A*B)
- ( A → ( C → B ) ) →( B + не C )
- (А→В) ↔ ( не В+ не А)
- A *( не A + B + C );
A
B
C
- A *(не A + B + C );
A
B
0
C
0
0
A
0
0
0
0
1
1
A+B
1
1
1
1
0
1
A+B+C
0
1
1
1
1
1
A*( A+B+C)
0
0
1
1
1
1
0
1
1
1
0
1
1
0
0
0
0
0
1
1
0
0
0
0
1
1
0
1
0
1
1
1
1
1
1
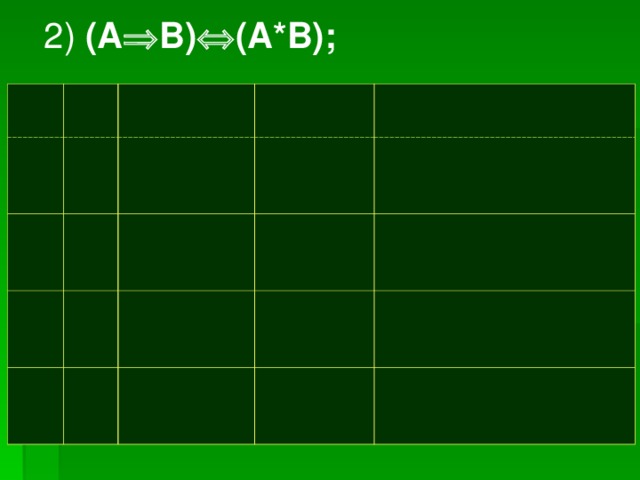
2) (A B) (A*B);
2) (A B) (A*B);
A
B
0
(A B)
0
0
(A*B)
1
1
1
1
0
1
0
(A B) (A*B)
0
1
0
0
0
0
1
1
1
1
3). ( A ( C B )) ( B +не C );
A
B
C
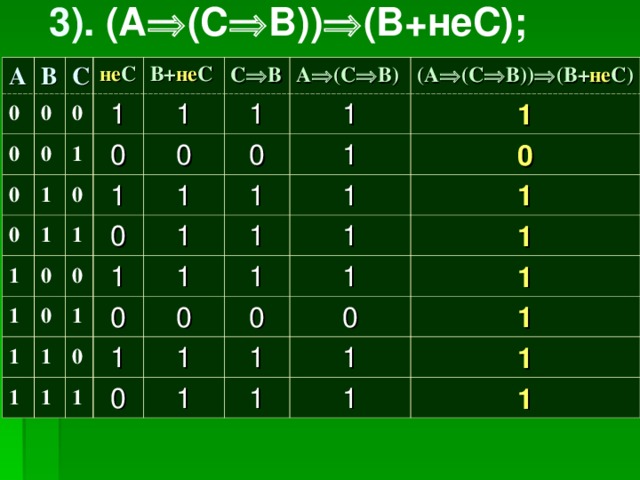
3). ( A ( C B )) ( B +не C );
A
0
B
C
0
0
0
не C
0
0
B+ не C
1
0
1
1
C B
1
1
0
0
1
1
A (C B)
0
1
1
0
1
(A (C B)) (B+ не C)
1
0
0
1
0
0
1
1
1
1
1
1
1
1
1
1
0
1
1
0
1
0
1
0
1
1
1
1
1
0
0
1
1
1
0
1
1
1
1
1
1
1
1
4). (А→В) ↔ (неВ+ неА)
A
B
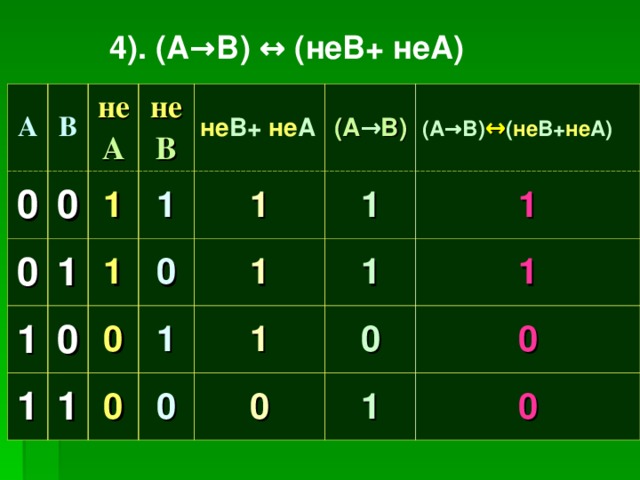
4). (А→В) ↔ (неВ+ неА)
A
B
0
не A
0
0
не B
1
1
1
не В+ не А
1
1
0
1
0
(A → B)
1
0
1
1
1
(А→В) ↔ ( не В+ не А)
1
0
1
1
1
0
1
0
0
0
1
0
Вебинар для учителей
Свидетельство об участии БЕСПЛАТНО!
