Повторение курса 10 класса.
Для итогового повторения курса геометрии 10 класса и входного повторения в начале 11 класса сделана подборка данных задач. Заучивание теорем и их доказательств не приводит к пониманию геометрии, а с помощью задач можно повторить теоретический курс, необходимый для входного контроля и дальнейшей работы с многогранниками и развивать пространственное воображение у обучающихся. Предложено достаточное количество однотипных задач, из которых можно составить самостоятельную работу по вариантам.
Перпендикуляр и наклонная к плоскости.
-
Отрезок АМ перпендикулярен плоскости квадрата АВСD, 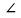 АВМ = 300. Найдите тангенс угла АСМ. [Ответ:
АВМ = 300. Найдите тангенс угла АСМ. [Ответ: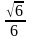 ]
]
-
Сторона квадрата равна 4 см. Точка, равноудаленная от всех вершин квадрата, находится на расстоянии 6 см от точки пересечения диагоналей. Найдите расстояние от этой точки до вершин квадрата. [Ответ: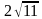 ]
]
-
Треугольник АВС – прямоугольный и равнобедренный с прямым углом С и гипотенузой 4 см. Отрезок СМ перпендикулярен плоскости треугольника и равен 2 см. Найдите расстояние от точки М до прямой АВ. [Ответ: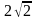 ]
]
-
Треугольник АВС – прямоугольный и равнобедренный с прямым углом С и гипотенузой 6 см. От резок СМ перпендикулярен плоскости треугольника; расстояние от точки М до прямой АВ равно 5 см. Найдите длину отрезка СМ. [Ответ: 4]
-
Треугольник АВС – прямоугольный и равнобедренный с прямым углом С и гипотенузой 8 см. От резок СМ перпендикулярен плоскости треугольника и равен 3 см. Найдите расстояние от точки М до прямой АВ. [Ответ: 5]
-
Треугольник АВС – прямоугольный и равнобедренный с прямым углом С и гипотенузой 6 см. Отрезок АМ перпендикулярен плоскости треугольника, 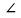 МСА = 600. Найдите длину отрезка МВ. [Ответ:
МСА = 600. Найдите длину отрезка МВ. [Ответ: 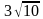 ]
]
-
Отрезок АВ имеет с плоскостью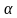 единственную общую точку А. Точка С делит его в отношении 2:1, считая от точки А. Через точки С и В проведены параллельные прямые, пересекающие плоскость
единственную общую точку А. Точка С делит его в отношении 2:1, считая от точки А. Через точки С и В проведены параллельные прямые, пересекающие плоскость 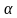 соответственно в точках С1 и В1. Длина отрезка АС1 равна 12 см. Найдите длину отрезка АВ1.[Ответ:18]
соответственно в точках С1 и В1. Длина отрезка АС1 равна 12 см. Найдите длину отрезка АВ1.[Ответ:18]
-
Отрезок АВ имеет с плоскостью 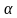 единственную общую точку А. Через его середину С и точку В проведены параллельные прямые, пересекающие плоскость
единственную общую точку А. Через его середину С и точку В проведены параллельные прямые, пересекающие плоскость 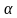 соответственно в точках С1 и В1. Длина отрезка АС1 равна 8 см. Найдите длину отрезка АВ1. [Ответ:16]
соответственно в точках С1 и В1. Длина отрезка АС1 равна 8 см. Найдите длину отрезка АВ1. [Ответ:16]
-
Середина С отрезка АВ принадлежит плоскости 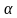 . Через концы отрезка АВ проведены параллельные прямые, пересекающие плоскость
. Через концы отрезка АВ проведены параллельные прямые, пересекающие плоскость 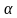 в точках А1 и В1. Длина отрезка А1С равна 8 см. Найти длину отрезкаА1В1.[Ответ: 16]
в точках А1 и В1. Длина отрезка А1С равна 8 см. Найти длину отрезкаА1В1.[Ответ: 16]
-
Отрезок АВ пересекает плоскость 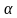 в точке С, которая делит его в отношении 3:1, считая от точки А. Через концы отрезка АВ проведены параллельные прямые, пересекающие плоскость
в точке С, которая делит его в отношении 3:1, считая от точки А. Через концы отрезка АВ проведены параллельные прямые, пересекающие плоскость 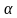 в точках А1 и В1. Длина отрезка А1С равна 15см. Найдите длину отрезка А1В1. [Ответ: 20]
в точках А1 и В1. Длина отрезка А1С равна 15см. Найдите длину отрезка А1В1. [Ответ: 20]
-
Через концы отрезка АВ, не пересекающего плоскость 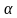 , проведены параллельные прямые, пересекающие плоскость
, проведены параллельные прямые, пересекающие плоскость 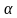 в точках А1 и В1 ; АА1 = 5см, В1В = 8 см. Найдите длину отрезка, соединяющего середины отрезков АВ и А1В1.[Ответ: 6,5]
в точках А1 и В1 ; АА1 = 5см, В1В = 8 см. Найдите длину отрезка, соединяющего середины отрезков АВ и А1В1.[Ответ: 6,5]
-
Отрезок АВ пересекает плоскость 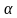 в точке С, которая делит его в отношении 3:5, считая от точки А. Через концы отрезка АВ проведены параллельные прямые, пересекающие плоскость
в точке С, которая делит его в отношении 3:5, считая от точки А. Через концы отрезка АВ проведены параллельные прямые, пересекающие плоскость 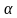 в точках А1 и В1. Длина отрезка А1С равна 12см. Найдите длину отрезка А1В1. [Ответ: 32]
в точках А1 и В1. Длина отрезка А1С равна 12см. Найдите длину отрезка А1В1. [Ответ: 32]
-
Из точки О пересечения диагоналей квадрата АВСD к его плоскости восстановлен перпендикуляр ОМ так, что 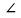 ОВМ = 600. Найдите косинус угла АВМ. [Ответ:
ОВМ = 600. Найдите косинус угла АВМ. [Ответ: 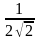 ]
]
-
Сторона квадрата АВСD равна 1 см. Отрезок АМ перпендикулярен плоскости квадрата, 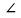 АВМ = 300. Найдите расстояние от точки М до прямой ВD. [Ответ:
АВМ = 300. Найдите расстояние от точки М до прямой ВD. [Ответ: 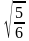 ]
]
-
Сторона квадрата равна 4 см. Точка, не принадлежащая плоскости квадрата, удалена от каждой из его вершин на расстояние 6 см. Найдите расстояние от этой точки до плоскости квадрата. [Ответ: 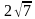 ]
]
-
Диагональ квадрата равна 6 см. Точка, равноудаленная от всех сторон квадрата, находится на расстоянии 5 см от точки пересечения его диагоналей. Найдите расстояние от этой точки до сторон квадрата. [Ответ: 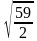 ]
]
-
Диагональ квадрата АВСD равна 10 см. Отрезок АМ перпендикулярен плоскости квадрата, угол АВМ равен 600. Найдите расстояние от точки М до прямой ВD. [Ответ: 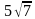 ]
]
-
В правильной четырехугольной пирамиде высота равна 12 см, а высота боковой грани – 15 см. Найдите боковое ребро. [Ответ:  ]
]
-
Основание пирамиды – прямоугольный треугольник с катетами 6 см и 8 см. Высота пирамиды проходит через середину гипотенузы треугольника и равна гипотенузе. Найдите боковые ребра пирамиды. [Ответ:  ]
]
-
Основанием пирамиды является прямоугольный треугольник, гипотенуза которого равна 15 см, а один из катетов – 9 см. Найдите площадь сечения, проведенного через середину высоты пирамиды параллельно её основанию. [Ответ: 13,5]
-
Три смежных ребра треугольной пирамиды попарно перпендикулярны и равны 6см, 6 см и 8см. Найдите площадь полной поверхности пирамиды. [Ответ: 66+ ]
]
-
В правильной четырехугольной пирамиде сторона основания равна 10 см, а боковое ребро – 13 см. Найдите высоту пирамиды. [Ответ:  ]
]
-
Основание пирамиды – прямоугольный треугольник с катетами 6 см и 8 см. Высота пирамиды, равная 12 см, делит гипотенузу этого треугольника пополам. Найдите боковые ребра пирамиды. [Ответ: 13]
-
В правильной треугольной пирамиде боковое ребро равно 10 см, а сторона основания 12 см. Найдите площадь полной поверхности пирамиды. [Ответ: 144]
-
Основание пирамиды – ромб с диагоналями 30 см и 40 см. Вершина пирамиды удалена от сторон основания на 13 см. Найдите высоту пирамиды. [(Ответ: 5]
-
По данной стороне основания a=9 и боковому ребру b=6 найти высоту правильной треугольной пирамиды. [Ответ: 3]
-
Во сколько раз увеличится боковая поверхность правильной треугольной пирамиды, если стороны основания увеличить в 2 раза, а апофему – в 3 раза. [Ответ: 6]
-
Плоский угол при вершине правильной треугольной пирамиды равен 90 . Площадь боковой поверхности пирамиды равна 3. Найти радиус окружности, описанной около боковой грани пирамиды. [Ответ: 1]
. Площадь боковой поверхности пирамиды равна 3. Найти радиус окружности, описанной около боковой грани пирамиды. [Ответ: 1]
-
По данной стороне основания a=8 и боковому ребру b=6 найти высоту правильной четырехугольной пирамиды. [Ответ: 2]
-
Высота правильной четырехугольной пирамиды равна 7, а сторона основания 8. Найдите боковое ребро. [Ответ:9]
-
Найдите площадь диагонального сечения правильной четырехугольной пирамиды, если сторона ее основания равна 1, а боковое ребро  . [Ответ: 2]
. [Ответ: 2]
-
Найдите полную поверхность правильной четырехугольной пирамиды, если высота ее равна 2 и сторона основания 4,2. [Ответ: 42]
-
Высота правильной четырехугольной пирамиды равна 12, а сторона основания равна 18. Найдите площадь боковой поверхности пирамиды. [ Ответ: 540]
-
Основанием пирамиды служит прямоугольник со сторонами 6 и 15. Высота пирамиды, равная 4, проходит через точку пересечения диагоналей основания. Найти площадь боковой поверхности пирамиды. [ Ответ: 126]
-
Боковая грань правильной четырехугольной пирамиды наклонена к плоскости основания под углом 60 . Площадь основания пирамиды 16. Найдите боковую поверхность пирамиды. [Ответ:32]
. Площадь основания пирамиды 16. Найдите боковую поверхность пирамиды. [Ответ:32]
-
Апофема правильной четырехугольной пирамиды равна 5. Тангенс двугранного угла при основании равен  . Найдите площадь полной поверхности пирамиды. [Ответ: 96]
. Найдите площадь полной поверхности пирамиды. [Ответ: 96]
-
Плоский угол при вершине правильной шестиугольной пирамиды равен 30 . Боковое ребро равно 2. Найдите боковую поверхность пирамиды. [Ответ: 6]
. Боковое ребро равно 2. Найдите боковую поверхность пирамиды. [Ответ: 6]
-
Стороны основания прямоугольного параллелепипеда равны 3 см и 5см, большая из диагоналей его боковых граней образует с плоскостью основания угол 600. Найдите площадь полной поверхности параллелепипеда. [Ответ:  ]
]
-
Площадь полной поверхности прямоугольного параллелепипеда равна 136 см2, а стороны основания 4 см и 6см. Вычислите диагональ прямоугольного параллелепипеда. [Ответ:  ]
]
-
Площадь полной поверхности прямоугольного параллелепипеда, в основании которого прямоугольник со сторонами 9 см и 6см, равна 408 см2. Найдите диагонали параллелепипеда. [Ответ:  ]
]
-
Найдите площадь диагонального сечения прямоугольного параллелепипеда, высота которого равна 12 см, а стороны основания 8 см и 6 см. [Ответ: 120]
-
Стороны основания прямоугольного параллелепипеда 3 и 4. Диагональ параллелепипеда образует с плоскостью основания угол 45 . Найдите полную поверхность параллелепипеда. [Ответ: 94]
. Найдите полную поверхность параллелепипеда. [Ответ: 94]
-
Диагональ прямоугольного параллелепипеда равна  и образует с плоскостью основания угол 45
и образует с плоскостью основания угол 45 . Найдите площадь боковой поверхности параллелепипеда, если площадь его основания равна 12. [Ответ: 70]
. Найдите площадь боковой поверхности параллелепипеда, если площадь его основания равна 12. [Ответ: 70]
-
Найти диагональ прямоугольного параллелепипеда, стороны основания которого 3 и 4, если она образует с плоскостью основания угол 60 . [Ответ: 10]
. [Ответ: 10]
-
Найдите площадь поверхности прямоугольного параллелепипеда, стороны основания которого 8 и 12 и образуют угол 30 а боковое ребро равно 6. [Ответ: 336]
а боковое ребро равно 6. [Ответ: 336]
-
В прямой треугольной призме стороны основания равны 3,4 и 5, а высота равна 6. Найдите ее полную поверхность.[ Ответ: 84]
-
В основании прямой призмы лежит равнобедренный прямоугольный треугольник, площадь которого равна 18. Найдите площадь боковой поверхности призмы, если ее высота равна ( ). [Ответ: 12]
). [Ответ: 12]
-
По стороне основания a=2 и боковому ребру b=3 найти полную поверхность правильной четырехугольной призмы. [Ответ: 32]
-
Найти полную поверхность правильной четырехугольной призмы, если ее диагональ равна  , а диагональ боковой грани 5. [Ответ: 66]
, а диагональ боковой грани 5. [Ответ: 66]
-
Найти боковую поверхность правильной шестиугольной призмы, наибольшая диагональ которой равна 13, а боковое ребро 5. [Ответ: 180]
-
Найти боковую поверхность правильной шестиугольной призмы, если сторона основания 3, а диагональ боковой грани 5. [Ответ: 72]
Призма.





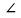 АВМ = 300. Найдите тангенс угла АСМ. [Ответ:
АВМ = 300. Найдите тангенс угла АСМ. [Ответ: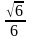 ]
]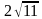 ]
]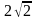 ]
]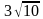 ]
] единственную общую точку А. Точка С делит его в отношении 2:1, считая от точки А. Через точки С и В проведены параллельные прямые, пересекающие плоскость
единственную общую точку А. Точка С делит его в отношении 2:1, считая от точки А. Через точки С и В проведены параллельные прямые, пересекающие плоскость 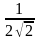 ]
]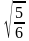 ]
]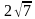 ]
]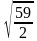 ]
]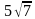 ]
]



















