Повторение. Метод координат в пространстве.

Дата

Тема: Повторение. Метод координат в пространстве.

Цели: систематизировать теоретические знания по теме; совершенствовать навыки решения задач.

Ход урока

1. АКТУАЛИЗАЦИЯ ЗНАНИЙ

Три попарно перпендикулярные прямые с выбранными направлениями и единицей измерения образуют систему координат в пространстве. Точка пересечения всех прямых является началом системы координат.

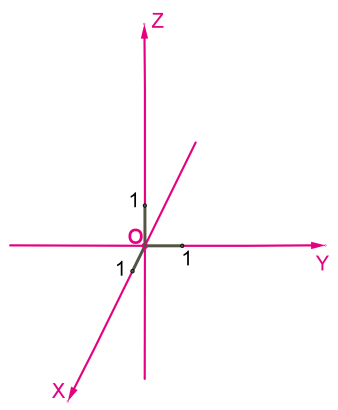
Оси координат Ox, Oy и Oz называются соответственно:

Ox — ось абсцисс, Oy —ось ординат, Oz — ось аппликат. 

Через две пересекающиеся прямые можно провести плоскость. Получаем три координатные плоскости: (Oxy), (Oyz) и (Oxz).

Положение точки A в пространстве определяется тремя координатами: x, y и z.

Если точка находится на оси Ox, то её координаты X(x;0;0).

Если точка находится на оси Oy, то её координаты Y(0;y;0).

Если точка находится на оси Oz, то её координаты Z(0;0;z).

Если точка находится в плоскости Oxy, то её координаты A₁(x;y;0).

Если точка находится в плоскости Oyz, то её координаты A₂(0;y;z).

Если точка находится в плоскости Oxz, то её координаты A₃(x;0;z).

Если в системе координат от начальной точки отложить единичные векторы  , , , то можно определить прямоугольный базис. Любой вектор можно разложить по единичным векторам и представить в виде  =x⋅ +y⋅ +z⋅ .

1. ПРАКТИЧЕСКАЯ ЧАСТЬ

Откройте свои тетради и запишите сегодняшнее число и тему урока. И приступаем к решению задач письменно.

Задача 1. Найти длину медианы АМ треугольника АВС, где А(0; 0; 3), в(2; 0; 0), С(4; -2; 2).

Решение. Найдем координаты точки М – середины отрезка ВС. По формуле нахождения координат середины отрезка

получаем, что

  .

По формуле нахождения длины вектора  получаем, что 

.

Ответ:  .

Задача 2. Определите вид треугольника АВС и найдите его периметр, если А(1; 0; 0), В(1; 3; 4), С(4; 3; 0).

Решение. По формуле длины отрезка найдем длины АВ, ВС и АС:

; 

Значит, треугольник равнобедренный, т. к. АВ=ВС.

.

Тогда периметр равен:

  .

Ответ: треугольник равнобедренный;  .

Задачи для самостоятельного решения

Задача 1. Даны координаты трёх точек A=(1;7;1), B=(1;7;3) и C=(7;9;7). Вычисли медианы AD,BE,CF треугольника ABC.

Задача 2. В координатной системе дана точка A(6;6;3). Определи расстояния точки от координатных осей OX, OY и OZ и от координатных плоскостей (XOY), (YOZ) и (XOZ).

Задача 3. В координатной системе дана точка A(6;8;2). Определи расстояния точки от координатных осей OX, OY и OZ и от координатных плоскостей (XOY), (YOZ) и (XOZ).

1. ПОДВЕДЕНИЕ ИТОГОВ УРОКА. РЕФЛЕКСИЯ

Домашнее задание: повторить теорию по теме, № 490, 509(б).