Просмотр содержимого документа
«урок 1 повторение тригонометрические функции и их свойства»
Алгебра и начала анализа
10 класс
УМК: А.Г. Мордкович Алгебра и начала математического анализа 10-11 классы в 2 ч. Ч. 1. Учебник;
А.Г. Мордкович Алгебра и начала математического анализа 10-11 классы в 2 ч. Ч. 2. задачник;
А.Г. Мордкович, П.В. Семенов Алгебра и начала математического анализа 10-11 классы. Методическое пособие для учителя.
Уровень обучения: базовый
Тема урока: Повторение. Тригонометрические функции и их свойства
Общее количество часов, отводимое на итоговое обобщающее повторение 12часов. На обобщение и повторение данной темы «Тригонометрические функции и их свойства» отводится 3 часа.
Урок № 1
Цели:
Образовательные: обобщить и систематизировать знания обучающихся по изученной теме, провести контроль уровня усвоения материала;
Развивающие: развитие математического мышления, интеллектуальных и познавательных способностей, развитие умения обосновать свое решение, контролировать и оценивать результаты своих действий;
Воспитательные: воспитание культуры общения, познавательной активности, чувства ответственности за выполненную работу, дисциплинированности, аккуратности, самостоятельности.
Задачи:
Обобщить представление о числовой окружности, о числовой окружности на координатной плоскости.
Отрабатывать умения находить значение синуса, косинуса на числовой окружности.
Отрабатывать навыки и умения построения графиков функций  ,
,  .
.
Развивать творческие способности в построении графиков функций  и
и  , зная
, зная  .
.
В результате изучения данной темы:
У учащихся формируются ключевые компетенции - способность самостоятельно действовать в ситуации неопределённости при решении актуальных для них проблем – умением мотивировано отказываться от образца, искать оригинальные решения
Учащихся демонстрируют теоретические и практические знания по теме: умение построения графиков тригонометрических функций и описания их свойств. Умеют, развернуто обосновывать суждения. Могут критически оценить информацию адекватно поставленной цели.
Учащиеся могут свободно пользоваться свойствами функций и строить графики сложных функций. Умеют передавать, информацию сжато, полно, выборочно. Умеют проводить самооценку собственных действий. Умеют самостоятельно выбрать критерии для сравнения, сопоставления, оценки и классификации объектов.
Оборудование и материалы для урока: мультипроектор, презентация для сопровождения урока, листы самоконтроля, карточки с текстом самостоятельной работы.
Тип урока: урок-тренинг
Ход урока.
I. Организационный момент.
II. Сообщение темы и целей урока
Сегодня на уроке мы обобщим и систематизируем имеющиеся знания по теме «Тригонометрические функции и их свойства». А всякое знание должно перейти в умение и навык. Проверим свои знания, умения и навыки, выясним пробелы и попытаемся их ликвидировать. Мы сегодня вспомним, как определять значение функции по значению аргумента при различных способах задания функции; строить графики изученных функций; описывать по графику и в простейших случаях по формуле поведение и свойства функций, находить по графику функции наибольшие и наименьшие значения.
Актуализация опорных знаний.
Работа по карточкам
| Вариант №1 | Вариант №2 |
| 1. Постройте график функции  ; ;
2. Укажите область значений данной функции;
3. Найдите наибольшее и наименьшее значения функции на интервале  | 1. Постройте график функции 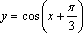 ; ;
2. Укажите промежутки возрастания и убывания функции;
3. Определите нули функции. |
Проверяем и сравниваем функции .
Какие свойства тригонометрических функций вы использовали при решении заданий?
| 1 вариант: y=sinx, обратите внимание на слайд. Область определения Точки пересечения с осями координат Четность и нечетность Промежутки монотонности Экстремумы Периодичность Промежутки знакопостоянства Множество значений
| 2 вариант:y=cos x, внимание на слайд. Область определения Точки пересечения с осями координат Четность и нечетность Промежутки монотонности Экстремумы Периодичность Промежутки знакопостоянства Множество значений
|
Практикум по решению задач
В одной системе координат построить графики функций одной группы и описать их свойства:
1)  ,
,  . 2)
. 2)  ,
, 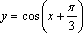 .
.
Обобщить преобразования графиков функций сдвигом по оси  .
.
В одной системе координат построить графики функций одной группы и описать их свойства:
1)  ,
,  . 2)
. 2)  ,
,  .
.
Докажите, что число  является периодом функции
является периодом функции  .
.
Докажите, что число  является периодом функции
является периодом функции  .
.
Найдите наименьший положительный период функции 
Найдите наименьший положительный период функции 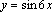
Переведите из градусной меры в радианную и расположите в порядке возрастания: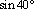 ,
,  ,
, ,
, .
.
Переведите из радианной меры в градусную и расположите в порядке убывания:
 ,
,  ,
,  .
.
Итог урока
Повторить свойства тангенса и котангенса.

















