Практическая работа №22 «Решение задач на теорему о трех перпендикулярах»

Практическая работа №22 «Решение задач на теорему о трех перпендикулярах»

Цель работы: Обобщить и систематизировать знания по теме «Перпендикулярность в пространстве»; закрепить умения использовать полученные знания для решения задач

Теоретические сведения к практической работе:

Опр. Две прямые в пространстве называются перпендикулярными, если угол между ними равен 90º.

Признак перпендикулярности прямой и плоскости

Если прямая перпендикулярна к двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна к этой плоскости.

В задачах часто используется теорема о 3-х перпендикулярах:

Прямая, проведённая в плоскости через основание наклонной перпендикулярно к её проекции на эту плоскость, перпендикулярна и к самой наклонной.

Обратная теорема

Прямая, проведённая в плоскости через основание наклонной перпендикулярно к ней, перпендикулярна и к её проекции.

Задания для самостоятельного решения:

Вариант 1

№1. Через вершину В квадрата ABCD проведена прямая BF перпендикулярно его плоскости. Найдите расстояние от точки F до вершины C, если BF=8 см, сторона квадрата равна 4 см.

№2. Дан прямоугольник ABCD. Через вершину Bпроведена прямая BM перпендикулярно к его плоскости. Найдите AD, если AM=5 см, MD=8см.

№3. Через точку О пересечения диагоналей квадрата со стороной 5 см проведена прямая ОК=6 см перпендикулярно к плоскости квадрата. Найдите расстояние от точки А до вершины квадрата

№4.Отрезок AD перпендикулярен к плоскости равнобедренного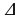 ABC, AB=AC=5, BC=6, AD=12, AE-высота 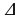ABC. Найдите AE, DE, BD, DC

Вариант 2

№1. Через вершину В квадрата ABCD проведена прямая BF перпендикулярно его плоскости. Найдите расстояние от точки F до вершины A, если BF=8 см, сторона квадрата равна 4 см.

№2. Дан прямоугольник ABCD. Через вершину Bпроведена прямая BM перпендикулярно к его плоскости. Найдите AD, если AM=3 см, MD=7см.

№3. Через точку О пересечения диагоналей квадрата со стороной 10 см проведена прямая ОК=5 см перпендикулярно к плоскости квадрата. Найдите расстояние от точки А до вершины квадрата.

№4.Отрезок AD перпендикулярен к плоскости равнобедренного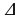 ABC, AB=AC=5, BC=6, AD=12, AE-высота 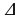ABC. Найдите AE, DE, BD, DC

Контрольные вопросы:

1. Какие две прямые называются перпендикулярными?

2. Сформулируйте признак перпендикулярности прямой и плоскости.

3. Сформулируйте теорему о трех перпендикулярах.